. (1.8)

где .

Углы атаки и скольжения, определяющие ориентацию вектора воздушной скорости ЛА, вычисляются в соответствии со следующими соотношениями:

(1.9)

где - вектор воздушной скорости ЛА в BF.

Рис. 1.2

В рамках данного проекта непосредственный пересчет векторов в скоростную систему координат не используется. Это связано с тем фактом, что все аэродинамические коэффициенты даны непосредственно в связанной системе координат и для определения компонентов аэродинамических сил и моментов необходимо определить лишь число Маха и углы атаки в каналах _Y=_I, _Z=_II, а также пространственный угол атаки _S:

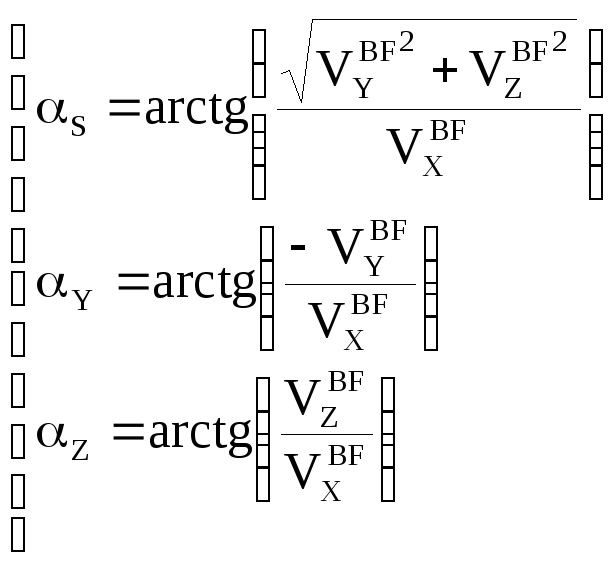(1.10)

где a – скорость звука на данной высоте.

Модель движения ла

Моделирование движения ЛА заключается в численном интегрировании полной системы дифференциальных уравнений движения центра масс ЛА и углового движения ЛА с учетом всей совокупности консервативных и управляющих сил и моментов, действующих на ЛА в процессе полета. Вследствие этого, возникают две относительно самостоятельные проблемы:

• построение наиболее приближенной к реальности модели силовых факторов;

• выбор и реализация метода численного интегрирования, обеспечивающего устойчивость и необходимую локальную погрешность численного решения, и, кроме того, обладающего высокой численной эффективностью, так как размерность задачи и сложность вычисления функции правых частей системы дифференциальных уравнений требуют существенных затрат вычислительных ресурсов.

Ниже подробно рассмотрена общая структура полной системы дифференциальных уравнений движения ЛА, модели силовых факторов и, применяемый в рамках данного проекта, метод численного интегрирования.

2.1. Уравнения движения центра масс ЛА

Пространственное движение центра масс ЛА описывается векторным уравнением сил в проекциях на оси IF:

. (2.1)

В этих уравнениях:

- вектор положения ЛА в IF;

- вектор скорости ЛА в IF;

- вектор суммы сил, действующих на ЛА, в проекциях на IF.

В скалярном виде эти уравнения можно переписать так:

, (2.2)

В число сил, действующих на ЛА, входят силы: притяжения Земли, тяги, аэродинамические и газодинамические силы, создаваемые газовыми рулями. Все эти силы, кроме силы тяжести, определяются в BF. Переход от вектора сил в BF к вектору сил в IFосуществляется с использованием матрицы перехода:

(2.3)

Уравнения углового движения

Пространственное угловое движение ЛА относительно центра масс описывается следующими уравнениями в проекциях на оси BF:

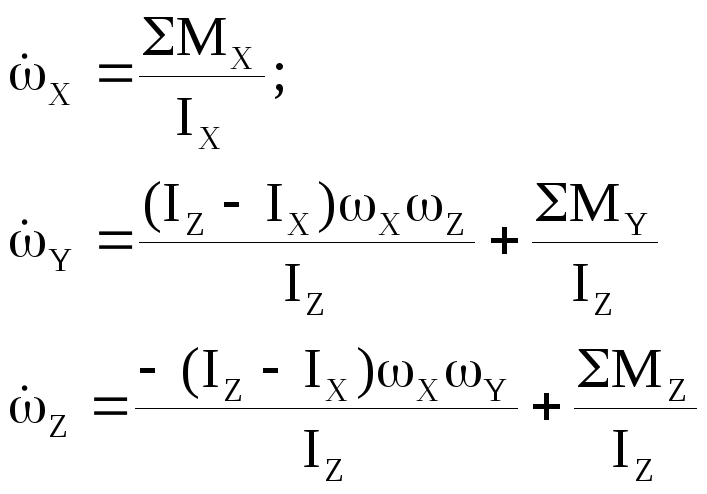(2.4)

В этих уравнениях:

- составляющие вектора угловой скорости ЛА относительно осей BF;

- составляющие суммарного вектора моментов , действующего на ЛА в полете, в проекциях на оси BF.

Здесь необходимо отметить, что для связи параметров углового движения, т.е. компонентов вектора угловой скорости в BF с параметрами движения центра масс ЛА вместо стандартных кинематических уравнений (1.3), приведенных в предыдущем разделе, будем использовать подход, основанный на применении параметров Родрига-Гамильтона. Данный подход базируется на представлении конечного поворота твердого тела в терминах собственного кватерниона преобразования систем координат, компоненты которого и получили название параметров Родрига-Гамильтона.

В соответствии с этим подходом параметры Родрига-Гамильтона связаны с углами Эйлера следующими соотношениями:

(2.5)

где Q – собственный кватернион преобразования между IF и BF, - знак кватернионного умножения.

Матрица перехода между IF и BF формируется на основе собственного кватерниона преобразования в соответствии со следующими соотношениями:

(2.6)

где q₁, q₂, q₃, q₄,- компоненты и модуль собственного кватерниона преобразования Q.

Традиционные углы Эйлера можно определить на основе данной матрицы перехода:

(2.7)

где a_ij– компоненты матрицы.

Тогда кинематические уравнения, т.е. уравнения, связывающие вектор угловой скорости вращения твердого тела с производными по времени от кинематических параметров запишутся следующим образом:

(2.8)

Данный подход, по сравнению с классическими кинематическими уравнениями (1.3), в силу линейности уравнений (2.8) позволяет получать высокоточное устойчивое численное решение, лишенное особых точек.

Таким образом, полная система дифференциальных уравнений, описывающих пространственное движение ЛА, состоит из 6^иуравнений движения центра масс (2.2), 3^хуравнений собственного углового движения ЛА (2.4) и 4^хкинематических уравнений (2.8), описывающих динамику параметров Родрига-Гамильтона.

Ниже подробно рассмотрена методика моделирования каждого из силовых факторов, входящих в уравнения (2.2, 2.4).

Сила притяжения Земли

В задачах рассматриваемого класса при рассмотрении относительно небольших дальностей полета допустимо использовать простейшую модель гравитационного поля Земли, не учитывающую нецентральность потенциала, а именно:

где g – ускорение, вызванное силой притяжения Земли на текущей высоте H; g₀ - ускорение, вызванное силой притяжения Земли на поверхности Земли, g₀ = 9.81 м/с.; R₀ – экваториальный радиус Земли, R₀ = 6371 км.

Необходимо отметить, что сила притяжения Земли не создает возмущающих моментов относительно центра масс ЛА, так как приложена непосредственно в т.ц.м.

Сила тяги ДУ и газодинамические моменты

Величина силы тяги, которая создается РДТТ, зависит от величины тяги при нулевых углах поворота газовых рулей и от углов поворота газовых рулей в текущий момент времении.

Кроме того, величина силы тяги меняется с высотой полета в соответствии со следующей зависимостью:

(2.9)

где R(t) – значение тяги РДТТ на текущей высоте H; R₀(t) - значение тяги РДТТ на уровне Земли; P(t) – атмосферное давление на текущей высоте H; P₀(t) – атмосферное давление на уровне Земли.

Закон изменения тяги при нулевых углах поворота газовых рулей на уровне Земли при анализе управляемого движения ЛА с достаточной точность может быть аппроксимирован зависимостью, показанной на рис.2.1.

Рис. 2.1. Закон изменения тяги при нулевых углах поворота газовых рулей

Тогда, компоненты силы тяги в BF при наличии газовых рулей, повернутых на ненулевые углы, могут быть описаны с помощью эмпирической зависимости следующего вида:

(2.10)

где, - вектор силы тяги в BF;- углы отклонения газовых рулей в I и II каналах и максимальный угол отклонения газовых рулей соответственно;- коэффициент потери тяги.

Сила тяги при ненулевых углах отклонения газовых рулей создает соответствующие управляющие моменты вокруг осей Y и Z BF. Эти управляющие моменты вычисляются по следующим соотношениям:

(2.11)

где, - управляющие газодинамические моменты вокруг осей Y и Z BF; LGF – плечо газовой силы;

XC₀ – относительное положение центра тяжести ЛА в момента старта; XC(t) – относительное положение центра тяжести ЛА в текущий момент времени; b_A – средняя аэродинамическая хорда.

Аэродинамические силы и моменты

Аэродинамические силы

Полная аэродинамическая сила задается ее проекциями на оси BF:

- вдоль оси ЛА (осевая аэродинамическая сила);

- нормальные аэродинамические силы, направленные по нормали к оси ЛА вдоль поперечных связанных осей ЛА Y и Z (рис. 2.2).

Рис. 2.2. Определение углов атаки и угла ориентации вектора скорости

Традиционно, эти силы определяются при помощи следующих соотношений:

, (2.12)

где: - характерная площадь (площадь крыльев) ЛА;- скоростной напор;

- величина скорости ЛА;

- проекции вектора скорости ЛА на оси BF, определяемые с помощью матричного соотношения:

(2.13)

- проекции скорости ЛА на оси IF, определяемые в результате интегрирования уравнений движения центра масс ЛА;

- коэффициенты осевой и нормальных аэродинамических сил.

Коэффициенты аэродинамических сил , в общем случае, задаются как функции пространственного угла атакии аэродинамического угла крена, определяющих ориентацию вектора скоростиотносительно осей BF. Кроме того, эти коэффициенты зависят от числа Махаи высоты полета ЛА.

Пространственный угол атаки ЛА определяется как угол между продольной осьюи вектором скорости ЛА(см. рис. 2.2). Соотношения для вычисления пространственного угла атаки ЛАи углов атаки в плоскостях связанных осей записываются следующим образом:

(2.14)

Пространственный угол крена определяет ориентацию вектора скорости ЛА относительно плоскостей крыльев. Этот угол рассчитывается с помощью соотношения:

, (2.15)

Также необходимо отметить, что в рамках данного проекта все аэродинамические коэффициенты даны для =45, так как ЛА большую часть своего полета находится именно в таком положении (схема X). Кроме того, вследствие этого при расчете всех аэродинамических коэффициентов, зависящих от углов атаки в каналах I и II, требуется перейти к фюзеляжным углам атаки, вычислить коэффициент, а затем снова спроецировать полученное выражение на данный канал. Данная методика соответствует следующим выражениям:

(2.16)

Коэффициент осевой аэродинамической силы

Коэффициент зависит от числа Маха, пространственного угла атакии высоты полета ЛА. Эта зависимость задается следующим выражением:

. (2.17)

Слагаемые, входящие в правую часть этой формулы, характеризуют различные составляющие осевой аэродинамической силы:

- коэффициент, характеризующий сопротивление ЛА при нулевом угле атаки (коэффициент лобового сопротивления);

- коэффициент, характеризующий индуктивное сопротивление ЛА;

- коэффициента донного сопротивления ЛА;

- коэффициенты, определяющие влияние углов атаки и поворота рулей на величину осевой силы.

Все перечисленные коэффициенты задаются в зависимости от их аргументов таблично. Значения этих коэффициентов при конкретных значениях аргументов рассчитываются путем интерполяции по ближайшим значениям из таблицы.

Коэффициенты нормальных аэродинамических сил

Коэффициенты нормальных аэродинамических сил в BF рассчитываются по методике описанной выше с использованием формулы (2.16) Значения этих коэффициентов при конкретных значениях аргументов рассчитываются путем интерполяции по ближайшим значениям из таблицы.

Особенность вычисления коэффициентов нормальных сил заключена в технологии определения коэффициента . Это связано с правилом знаков при определении угла атаки, т.е. на положительное значение угла атаки коэффициент нормальной силы отрицательный. Иными словами:

.

2.5.2. Аэродинамические моменты

В полете на ЛА действуют аэродинамические моменты относительно осей BF, определяемые соотношениями:

(2.18)

где - характерный размер (средняя аэродинамическая хорда крыла) ЛА;

- характерный размер (размах крыльев) ЛА; S - характерная площадь (площадь крыльев) ЛА.

- коэффициенты моментов от аэродинамических сил относительно осей BF.

Коэффициент момента крена

Коэффициент момента крена m_xопределяется соотношением:

(2.19)

где - коэффициент момента косого обдува, возникающего вследствие неравномерного обтекания плоскостей крыльев ЛА при отклонении аэродинамических рулей;- коэффициент момента крена, вызванного отклонением элеронов;- коэффициент демпфирующего момент крена.

Коэффициент момента косого обдува вычисляется по формуле:

(2.20)

где - табличные функции числа Маха и пространственного угла атаки, учитывающие влияние углов атаки отклонения рулей на значение коэффициента момента косого обдува.

Коэффициент момента крена, вызванного отклонением элеронов, вычисляется по формуле:

(2.21)

где - табличная функция числа Маха и пространственного угла атаки, учитывающая влияние отклонения элеронов на коэффициент момента крена;- угол отклонения элеронов;- максимальный угол отклонения элеронов.

Коэффициент демпфирующего момента крена вычисляется по формуле:

(2.22)

где - коэффициент вращательной производной момента крена по угловой скорости;_x – угловая скорость ЛА вокруг оси X BF.

Коэффициенты момента относительно поперечных осей

Коэффициенты момента относительно поперечных осей определяются соотношениями:

(2.23)

где - коэффициенты демпфирующих моментов относительно осей Y и Z;- коэффициенты момента относительно поперечных осей, пропорциональные углам атаки в каналах и отклонениям рулей при начальной центровке ЛА. Данные коэффициенты вычисляются аналогично коэффициентам нормальных аэродинамических сил, т.е. по формуле (2.16). Обратный знаки длявведен по аналогии с коэффициентом нормальной аэродинамической силы C_z в с связи с правилом знаков для канала Z.

Коэффициенты демпфирующих моментов относительно осей Y и Z рассчитываются по формулам:

(2.24)

где - коэффициенты вращательной производной моментов относительно поперечных осей по угловой скорости;_Y,_Z– угловые скорости ЛА вокруг осейYиZBF соответственно.

Модель атмосферы Земли

В рамках данной работы использовалась модель Временной Стандартной атмосферы СА-72, позволяющая вычислять для текущей высоты H плотность атмосферы , скорость звука а и давление атмосферы P в диапазоне высот 0-120км над уровнем моря. Для повышения вычислительной эффективности процесса моделирования движения ЛА все три необходимые характеристики были представлены разложением в ряд по полиномам Чебышева в указанном диапазоне высот.

Массово-инерционные характеристики

Такими характеристиками являются:

• - масса ЛА;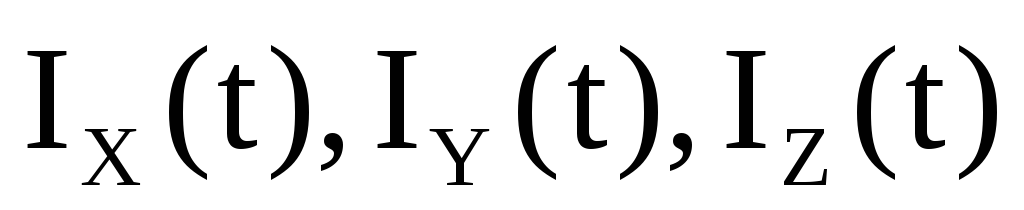

• - моменты инерции ЛА относительно связанных осей;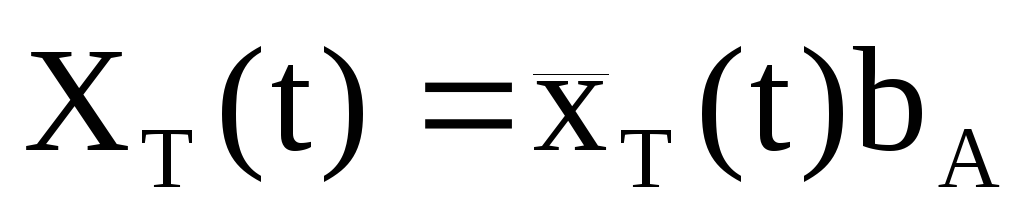

• - положение центра масс ЛА.

Все перечисленные характеристики являются переменными на активном участке полета из-за выгорания топлива и остаются постоянными на пассивном. При моделировании движения ЛА их изменение на активном участке можно полагать происходящим по линейному закону (см., например, рис. 2.3 для массы ЛА), зависящему от начального и конечного значений параметра, а также от длительности активного участка.

Рис. 2.3. Закон изменения массы ЛА по времени

На этом графике - начальная масса ЛА;- масса ЛА без топлива.

В рамках данного проекта будем полагать, что все остальные массово-инерционные характеристики изменяются по времени аналогичным образом.

Метод численного интегрирования уравнений движения ЛА

В рамках данного проекта в качестве метода численного интегрирования уравнений движения ЛА используется метод прогноза-коррекции Адамса-Мултона-Башфорта. Этот метод определяется следующими соотношениями:

1. Рассматривается система обыкновенных дифференциальных уравнений вида:

2. Основной шаг метода интегрирования ():

а) Прогноз: - явный метод Адамса (метод Эйлера);

б) Вычисление правых частей: ;

в) Коррекция: - неявный метод Адамса (правило средней точки);

2. Подшаги б) и в) повторяются до сходимости или до максимального числа итераций. Сходимость определяется соотношением:

, (2.25)

где к - номер итерации, - локальная погрешность интегрирования на шаге.

Особенность этого метода состоит в совместном использовании явного и неявного метода Адамса, что позволяет существенно повысить точность интегрирования, и, кроме того, избежать эффекта "запаздывания" численного решения при использовании в процессе интегрирования некоторой измерительной информации.

Отметим также, что для обеспечения корректного совместного интегрирования разнородных по физической природе уравнений ("медленное" движение центра масс и "быстрое" угловое движение) формула (2.25) дополнена соответствующим механизмом калибрующих весов:

, (2.26)

где W- матрица весовых коэффициентов, позволяющая повысить требования по локальной погрешности интегрирования к определенным компонентам расширенного фазового вектора (например, при стандартном коэффициенте 1 для уравнений движения центра масс и локальной точности 110^-6, весовой коэффициент для уравнений углового движения выбран равным 1000, что на три порядка увеличивает требования по точности).

СИСТЕМА СТАБИЛИЗАЦИИ

Для ЛА рассматриваемого класса система стабилизации должна удовлетворять следующим требованиям:

• обеспечение устойчивости углового пространственного движения ЛА;

• парирование возмущающих моментов и отработку значений нормальной перегрузки в поперечных каналах, задаваемых системой наведения;

• требуемые динамические характеристики контура стабилизации в составе системы наведения по быстродействию и перерегулированию;

• отработку стартовых возмущений на начальном участке полета;

• ограничение в полете перегрузки ЛА, его угла атаки и углов поворота рулей и элеронов.

В технических заданиях на проектирование ЛА рассматриваемого класса обычно предъявляют следующие требования к динамическим свойствам системы стабилизации:

• время переходного процесса 0.05 с на режиме максимального скоростного напора;

• время переходного процесса 0.2…0.4 с при минимальном скоростном напоре на активном и пассивном участках полета;

• допустимое перерегулирование 10…20%;

• стабильность коэффициента передачи по перегрузке .

Требование по быстродействию является основным.

Общая структура системы

Система стабилизации ЛА строится по традиционной схеме. Она состоит из трех независимых каналов относительно связанных осей, причем продольные каналы практически идентичны (рис. 3.1).

В качестве измерителей в системе стабилизации используются датчики угловой скорости (ДУСы), акселерометры (датчики линейных ускорений - ДЛУ), а также датчики угла атаки.

В качестве исполнительных устройств применяются газовые рулевые приводы, управляющие положением аэродинамических и газовых рулей в продольных каналах, а также аэродинамических органов управления движением крена - элеронов.

Всего в составе системы стабилизации 7 датчиков и 3 рулевых привода.

Сигналы обратных связей формируются с использованием цифровых устройств.

Рис. 3.1. Состав и структура системы стабилизации ЛА

Структура системы в продольных каналах

Как указывалось выше, к системе стабилизации в продольных каналах предъявляются жесткие требования по качеству регулирования при выполнении команд наведения в присутствии возмущающих моментов. Среди различных мер, применяемых для выполнения этих требований, основными являются:

• формирование системы стабилизации в продольных каналах в виде системы с обратными связями по угловой скорости, перегрузке ЛА и углу атаки;

• введение нелинейных корректирующих устройств во входную цепь и в замкнутый контур системы, сформированных с использованием принципов теории систем с переменной структурой.

Структурная схема одного из продольных каналов системы стабилизации приведена на рис. 3.2.

Рис. 3.2. Состав и структура продольного канала системы стабилизации

Структура системы в канале крена

Для ЛА рассматриваемого класса предъявляются требования по стабилизации не угла, а угловой скорости вращения по крену. При этом для ЛА как объекта управления особенностью является высокая частота слабо демпфированных колебаний по крену, что связано с малым моментом инерцииЛА относительно оси.

Задача системы стабилизации в канале крена состоит в том, чтобы обеспечить условия, при которых сохраняется нормальное функционирование координатора цели и требуемая точность самонаведения при угловых колебаниях корпуса ЛА.

Одной их особенностей системы стабилизации по крену для ЛА рассматриваемого класса является компенсация момента косого обдува.

Блок-схема системы стабилизации по крену представлена на рис. 3.3.