Лабораторная работа №4 «Оптимизация сети наземных измерительных пунктов в целях повышения точности определения параметров орбит исз»

Задание

Целью данной лабораторной работы является изучение основ теории планирования навигационного эксперимента и методики априорного анализа точности в целях повышения точности навигационных определений. В работе рассматривается планирование работы навигационных средств сети наземных станций, осуществляющих поддержку орбитальной группировки системы КА. Работа проводится с использованием специального программного обеспечения «Планировщик сети НИП», предназначенного для обеспечения следующих функций:

• Определение зон радиовидимости.

• Определение апостериорной ковариационной матрицы спутникового созвездия в абсолютных декартовых или орбитальных координатах, в зависимости от заданного планирования работы НИП.

• Определение общего времени работы НИП, обеспечивающего необходимый уровень точности определения орбит спутников созвездия.

• Планирование работы сети НИП для минимизации среднеквадратического отклонения ошибок положения спутников созвездия на орбите.

• Планирование работы сети НИП в случае одновременного обслуживания нескольких спутниковых созвездий.

Требуется рассчитать на заданный период оптимальный план работы навигационных средств сети НИП по указанному созвездию КА в соответствии с выбранным критерием оптимальности.

Указания к выполнению

Общие характеристики пмо

Планировщик работы сети НИП разработан для планирования работы сети наземных измерительных пунктов (НИП). Целью планирования является обеспечение необходимого уровня точности определения орбиты созвездия спутников за счет минимизации времени работы наземного измерительного пункта, с учетом необходимых технических ограничений, таких, как условия радиовидимости, время переключения антенны измерительного пункта и т.д.

Формулировка задачи

Рассмотрим произвольное созвездие спутников. Предположим, что отклонения начальных условий движения спутников созвездия от номинальных (заданных) условий являются случайными величинами.

Введем также понятие “сеть НИП”, которая, по существу, является сетью, состоящей из используемых наземных измерительных пунктов, включенных в эксперимент.

Предположим также, что все навигационные измерения организованы как сеансы измерений стандартной продолжительности. Частота измерений во время сеанса является постоянной. Сеансы измерений могут быть осуществлены, если выполнены условия радиовидимости спутника, соответствующие данному НИП, принадлежащему рассматриваемой сети, и данный спутник входит в рассматриваемое созвездие. Таким образом, расходы на проведение измерений могут быть определены из общего числа сеансов измерений.

Кроме того, предположим, что вся информация, полученная в течение всех сеансов измерений, используется для определения орбиты спутников созвездия с использованием метода наименьших квадратов, либо метода Калмановской фильтрации.

Однако, сразу несколько спутников созвездия не могут наблюдаться данным НИП одновременно. Это обстоятельство определяет следующую особенность задачи планировки работы НИП: необходимо определить за минимальное время положение каждого из спутников созвездия на орбите. Таким образом, решение задачи планирования работы НИП должно содержать планирование перенацеливания антенн НИП сети с одного спутника созвездия на другой, с учетом "времени переключения" и ограничения максимальной последовательности сеансов наблюдения.

Задача состоит в определении плана работы НИП, который позволит обеспечить заданную точность определения положения спутников созвездия на орбите за минимальное время работы.

Введем также вариацию скалярного параметра l, которая характеризует отклонение положения спутников созвездия вдоль орбиты от заданного в баллистической структуре созвездия как характеристику точности работы сети НИП по рассматриваемому созвездию. Практика показывает, что наиболее сложным является уточнение именного этого параметра для спутника, находящегося на почти круговой орбите.

Основные определения.Положим, что процесс выполнения измерительного сеанса НИП протекает согласно рис. 1.

Н

Рис. 1. Основные определения

а этом рисунке приняты следующие обозначения.

Зона радиовидимости спутника #k- это интервал времени[T^(k)_inpT^(k)_out], в течение которого спутник может непосредственно наблюдаться данным НИП, с учетом оговоренных ниже технических ограничений, наложенных на угол обзора НИП. Здесь T^(k)_inpи T^(k)_out- обозначения соответственно начального и конечного моментов зоны радиовидимости #k.

Сеанс измерения- временной интервал, в течение которого проводится определенное число измерений согласно специальным функциям НИП. Как правило, после каждого сеанса измерений существует пауза для восстановления функциональности оборудования НИП (так называемый период восстановления). Здесь и далее будем использовать следующие предположения относительно технических ограничений НИП:

• начало первого сеанса измерения в каждой зоне радиовидимости совпадает с началом данной зоны;

• период восстановления равен установленной наперед величине, которая может быть изменена с использованием базы данных;

• максимальная последовательность навигационных групп (сессий) не должна превышать заданную;

• для перенацелевания антенны НИП с одного наблюдаемого спутника на другой в той же зоне радиовидимости необходим определенный интервал времени, называемый здесь и далее "временем переключения";

• все измерения в сеансе измерения распределены равномерно.

Нормальная точкаt_norm сеанса измерения - это момент времени, который определяет момент коррекции ковариационной матрицы расширенного вектора состояния спутников созвездия по результатам обработки измерений, полученных в данном сеансе.

План навигационных измеренийзадается таблицей (матрицей) следующего вида:

Таблица 1

Номер НИП	Сеанс измерений #1 (t(1)on t(1)off)	Сеанс измерений #2 (t(2)on t(2)off)		Сеанс измерений #Ns (t(Ns)on t(Ns)off)
1	SC #1	SC #1		SC #4
2	SC #4	SC #5		SC #1
				
NTS	SC #7	SC #7		SC #9

Таким образом, план работы для данной сети НИП есть матрица (или набор векторов). Каждая строка данной матрицы в сущности представляет собой план работы данного НИП, или, иначе говоря, программу переключений антенны НИП в пределах зоны радиовидимости. Эта программа переключений содержит несколько наблюдаемых спутников, а также время начала и завершения наблюдений (t_onи t_offсеанса измерений соответственно).

В итоге, каждый сеанс измерений из общего числа сеансов данного НИП получает соответственно номер наблюдаемого созвездия спутников.

Планирование работы НИП.

Чтобы обеспечить заданную точность определения положения спутников созвездия, необходимо управлять процессом обработки (фильтрации) данных. Точнее, необходимо управлять процессом вычисления апостериорной ковариационной матрицы расширенного вектора состояния спутников созвездия, который включает, помимо вектора состояния спутника, также некоторые дополнительные составляющие, такие, как систематическая ошибка измерений НИП.

Процесс изменения априорной (прогнозируемой) и апостериорной (уточненной)ковариационных матриц может быть описан дискретным алгоритмом Калмановской фильтрации (который эквивалентен рекурсивному алгоритму метода наименьших квадратов) [4]:

, i = 0, 1, , N_s(1)

где

индекс "i" означает принадлежность соответствующей матрицы к моменту времениt_i, который, по существу, является номером нормальной точки в данном сеансе измерений. Таким образом, мы рассматриваем не единичные навигационные измерения или, так называемые, "кванты измерений", являющиеся частью сеанса измерения, а исключительно целые сеансы измерений. Другими словами, мы предполагаем, что все навигационные измерения, заключенные в данном сеансе измерений, выполняются в момент времениt_i , являющийся нормальной точкой данного сеанса.

_i,_i-1- фундаментальная матрица уравнений движения спутников созвездия, линеаризованная в окрестности опорной круговой орбиты. (более подробная информация изложена в разделе 2.4.2).

H_i = - матрица частных производных измеряемых (навигационных) параметров взятых по компонентам расширенного вектора состояния спутников созвездия (более подробная информация изложена в разделе 2.4.2).

- ковариационная матрица случайных ошибок измерения.

_I- план навигационных измерений, формализующий процесс работы НИП в момент времениt_iнепосредственно соответствующий приведенной выше таблице.

Возможность планирования работы НИП состоит в выборе последовательности _i , которая формализует план навигационных измерений. Здесь предполагается, что каждый НИП, участвующий в наблюдениях, поддерживает навигационные параметры, измеряемые сходным образом.

Также предполагается, что задана априорная ковариационная матрица , необходимая для начала вычислений согласно (1).

Задача состоит в нахождении плана ^* для обеспечения позиционирования каждого из спутников созвездия на орбите с заданной точностью за минимальное времяT:

(2)

где

J– критерий точности.

l- отклонениеj-того спутника созвездия от заданной точки на орбите.

- среднеквадратическое отклонениеj-того спутника созвездия от заданной точки на орбите.

^* - заданное значение данного среднеквадратического отклонения.

- общее число спутников созвездия.

Величина отклонения позиционирования спутника (квадрат среднеквадратического отклонения) должна быть определена в орбитальной системе отсчета, тогда как движение спутников созвездия задано в инерциальной системе отсчета (ИСО) /см. раздел 2.4.1/. В результате связь между апостериорной ковариационной матрицей , полученной по алгоритму обработки данных и отклонением позиционирования имеет следующий вид:

где

_j, i_j- долгота восходящего узла и наклонение опорной орбиты спутника

j-того спутника.

Индекс Тапостериорной ковариационной матрицы расширенного вектора состояния спутника обозначает конечный момент времени, выбранный для определения. В результате, задача оптимального планирования может рассматриваться как задача оптимального программного управления динамическим объектом, описанным соотношениями (1).

Для решения этой задачи воспользуемся специальное подходом, разработанным авторами [4], основанным на использовании аналитических свойств уравнения Риккати и позволяющим провести эквивалентное преобразование изначально нелинейной задачи оптимизации к линейной. Полностью данный подход был опубликован в [4], и в настоящее время широко используется при рассмотрении задач оптимизации.

Согласно рассматриваемому подходу эквивалентная задача оптимального планирования нелинейного объекта (1), записывается для линейного динамического объекта, имеющего в качестве фазовых координат последовательности векторов {s_i} и {q_i} и соответствует соотношениям:

, (3)

где индекс "Т" в обозначении фундаментальной матрицы означает конечный момент времениТ.

Начальные условия для этого соотношения:

P_0,Nss₀- q₀= 0,

где .

Индекс N_sобозначает номер конечного момента времениТ, который совпадает с нормальной точкой последнего сеанса измерений.

Для любого i-того момента времени имеем

P_i,Nss_i- q_i= 0.

В [4] доказано, что изначально сформулированная задача оптимизации эквивалентна следующей задаче:

(4)

с краевыми условиями s_T= ||B^(j)|| и, j = 1, 2,,(5)

Задача оптимального планирования наблюдений для каждого НИП рассматривается отдельно. После нахождения планы работы сравниваются и объединяются для получения оптимального плана сети.

Рассмотрим решение задачи оптимального планирования для изолированного спутника созвездия.

Для решения задачи оптимизации (2) или эквивалентной ей задачи (4), используем частное решение обратной задачи оптимизации:

(6)

за счет изменения общего времени планирования работы наземного комплекса, принимая во внимание все выше оговоренные технические ограничения на условия наблюдения, время переключения и т.д.

Вообще говоря, нет необходимости достигать минимального значения J^*; достаточно лишь обеспечить выполнение условия:

(7)

Согласно упомянутому выше подходу [4], для решения задачи (6) используем преобразование к эквивалентной задаче для динамического объекта (3) для изолированного спутника по критерию

(8)

и ограничению s_T = B.

Для решения эквивалентной задачи (8) используем принцип максимума Понтрягина и запишем гамильтониан системы (3):

, (9)

где

 - множитель Лагранжа, соответствующий ограничению , (10)

^*- допустимая общая продолжительность сеансов измерений.

Уравнения, сопряженные с (3), приведены в [4]:

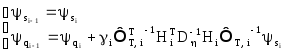(11)

где

- сопряженные переменные, относящиеся к фазовым переменным {s_i} и {q_i} в (3).

Краевые условия для (11):

(12)

Для максимизации гамильтониана (9) определим последовательность {_i}следующим образом:

, (13)

где

- набор дискретных моментов времени, которые соответствуют максимальному значению так называемой "программной функции" , причем каждый элемент последовательности задается формулой:

(14)

- множитель при _iиз формулы для гамильтониана (9), задающий ограничения процесса наблюдения (общее число измерений, общая продолжительность зон наблюдения и т.д.).

Численный алгоритм оптимального планирования.

Обобщая вышесказанное, сформулируем следующий алгоритм планирования при минимизировании критерия точности (6):

1. Для каждого НИП, входящего в сеть НИП, определяются зоны радиовидимости. Планирование осуществляется только для тех зон, где могут наблюдаться более, чем два спутника созвездия.

2. В отмеченных согласно пункту 1 зонах радиовидимости вычисляется соответствующая наблюдаемым спутникам созвездия "программная функция” M₁, M₂^,Затем, для каждого сеанса наблюдений в данной зоне радиовидимости определяется максимальный элемент полученной ранее последовательности программной функции. Этот элемент определяет план нацеливания антенны НИП (рис. 2).

3. Если один и тот же спутник может наблюдаться различными НИП, соответствующие программные функции, полученные для разных НИП и одного и того же спутника, сравниваются. Максимальная программная функция определяет оптимальный план работы для различных НИП в приложении к данному спутнику (рис. 3).

4. Процедуры, описанные в пунктах 2 и 3 могут быть повторены для обеспечения заданного значения критерия оптимальности или для подсчета значения критерия для общего времени работы данного НИП.

5. После завершения процедуры планирования на интервале планирования осуществляется проверка построенного плана измерений для каждого НИПа в отдельности, а именно, начиная с начала интервала последовательно проверяются пустые (свободные от измерений) и заполненные участки зон видимости с целью обеспечения требуемых ограничений на время переключения антенны и максимальное значение последовательности навигационных сеансов (групп). При этом при неудовлетворительном результате проверки “выбрасываются” из плана те навигационные сеансы, у которых значение программной функции меньше.

Рис. 2. Формирование плана работы для одного НИП

M_НИП1, M_НИП2- соответствующие программные функции.

Рис.3. Формирование плана работы для двух НИП

Системы координат.

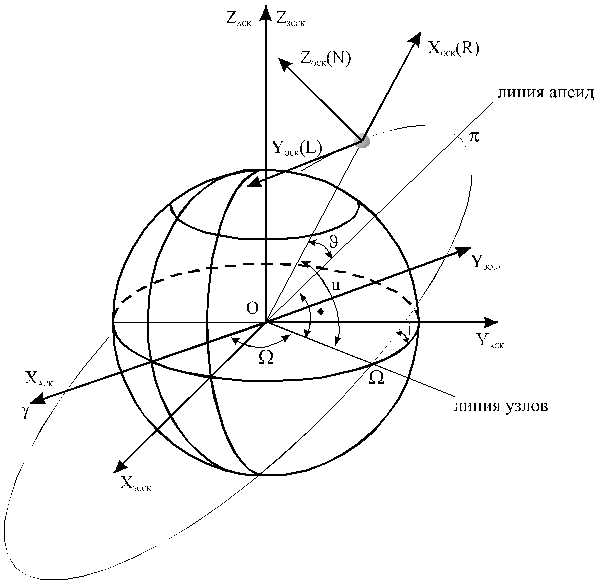
Планировщик работы НИП использует те же стандартные системы координат, как и, например, программа МДС. (см. рис. 4).

Абсолютная инерциальная система координат 2000 (ИСК 2000, IF2000)

Начало этой системы координат совпадает с центром масс Земли. Основная плоскость совпадает с плоскостью экватора на 0 часов 00 минут 00 секунд 1 января 2000 года (так называемая эпоха 2000.0). Ось X_АСКэтой системы координат направлена в точку весеннего равноденствия эпохи 2000.0. Ось Z_АСКнаправлена на северный полюс мира и проходит через Международное Условное Начало 1900-1905г.г. Ось Y_АСК дополняет эту систему до правой.

Земная связанная система координат (ЗССК, UGF)

Начало этой системы координат совпадает с центром Земли. Ось Z_ЗССКнаправлена на северный полюс мира и проходит через Международное Условное Начало 1900-1905г.г. Ось X_ЗССКпроходит через Гринвичский меридиан, соответствующий Международному Условному Началу, ось Y_ЗССКдополняет эту систему до правой.

Орбитальная система координат (ОСК, OF)

Начало этой системы координат совпадает с центром масс ИСЗ созвездия. Ось X_ОСКнаправлена по радиус-вектору ИСЗ (так называемая R-ось); ось Z_ОСКнаправлена по вектору Лапласа ИСЗ (так называемая N-ось); осьY_ОСКдополняет эту систему до правой(так называемая L-ось).

Гринвичская система координат (GF, ГСК)

Отличие Гринвичской системы координат от Единой географической состоит в определении положения северного полюса Земли: здесь используется положение так называемого истинного полюса Земли, в отличие от Единой географической системы, где используется Международное условное начало (ICO).

Рис. 4. Системы координат

Математическая модель движения спутников созвездия.

В данной программе используется математическая модель движения спутников созвездия в виде стандартных дифференциальных уравнений движения небесного тела в центральном гравитационном поле:

(15)

,

где x,y,z- координаты центра масс спутника в абсолютной системе отсчета

- радиус-вектор спутника,

- гравитационная постоянная Земли.

Введем вектор состояния спутника в виде

В результате получим уравнение движения спутника в векторной форме:

,

Согласно принятому подходу, для решения задачи оптимального планирования будем использовать следующую линейную модель движения спутников созвездия:

(16)

где x_i- отклонение вектора состояния от номинального значения в момент времениt_i.

Помимо этого в состав компонент расширенного вектора состояния необходимо включить систематические ошибки навигационных измерений (см. ниже в разделе 2.4.4)

Таким образом, общая размерность расширенного вектора состояния будет равна:

6(компоненты положения +компоненты скорости) + mr,

где m- число навигационных параметров, измеряемых данным НИП и, как следствие, число систематических ошибок этих измерений; например, если можно измерить только дальность и скорость изменения дальности, тоmравно 2 в случае совместного планирования по дальности и скорости изменения дальности и 1 в случае независимого планирования по дальности и скорости изменения дальности. Действительно, если выполняется независимое планирование по дальности и скорости изменения дальности,mравно 1 для дальности и скорости изменения дальности соответственно.

r- число НИП, используемых для определения орбиты спутника.

Следовательно, расширенный вектор состояния x_i будет иметь следующую структуру:

Начальные условия для системы (16) - гауссовский случайный вектор X(0):

,

где - вектор размерности 6 +mr, состоящий из двух блоков,

- априорная ковариационная матрица размерности [6+mr][6+mr]

Фундаментальная матрица Ф_i,i-1, соответствующая расширенному вектору состояния, определена как матрица размерности [6+rm][6+rm] и задана в виде:

Уравнения (16) используются для вычисления фундаментальной (переходной) матрицы в следующем виде:

, (17)

где t_i-1- начальный момент времени,

t_{i -} конечный момент времени,

I- единичная матрица 66,

A(t)- матрица линеаризованной системы (15):

(18)

Элементы матрицы A(t_i)вычисляются в окрестности опорной траектории круговой орбиты спутника созвездия. В качестве опорной может быть принята, например, орбита, полученная на основе эфемерид.

Предположим, что начальные условия уравнений (15) - случайный вектор, компоненты которого распределены по гауссовскому закону с математическим ожиданием, совпадающим с вектором эфемерид в заданный момент времени t₀, полученный с помощью программы МДС, и априорная ковариационная матрица размерности 66, которую должен задать пользователь.

Формирование начальных условий составляющей X_sрасширенного вектора состояния так же, как и для матрицы рассмотрено ниже в разделе 2.4.4

Модель движения наземного измерительного пункта.

Чтобы обеспечить определение орбиты спутников созвездия, так же как и плана работы НИП, необходимо определить положение НИП в инерциальной системе координат, которое используется для численного интегрирования уравнений движения спутников.

Однако, НИП расположен на поверхности Земли, и таким образом, для определения его положения в инерциальной системе координат необходимо рассмотреть так называемую задачу преобразования координат.

Эта задача решается с использованием следующих переходных матриц [2,3]:

• матрица прецессии,

• матрица нутации,

• матрица учета поворота на звездное временя,

• матрица учета смещения истинного полюса Земли.

В качестве начальных данных для решения задачи преобразования координат примем положение НИП в единой географической системе координат (UGF). Для определения положения НИП, например, в инерциальной системе 2000 (IF2000), необходимо провести следующие вычисления [2]:

• “повернуть” UGFдо совпадения сIAFна угол, соответствующий истинному звездному времени Гринвичского меридиана.

• “повернуть” IAFдля коррекции к экватору и точке весеннего равноденствия эпохиIF(например, эпохи 2000).ы

Чтобы определить истинное положение НИП в гринвичских координатах (GF) , необходимо провести следующие вычисления:

• “повернуть” UGFдо нового положения истинного положения полюса Земли, который определяется гринвичскими координатами.

Все процедуры, необходимые для вычисления рассматриваемых матриц, приведены в Приложении. Здесь даются только окончательные формулы для определения положения НИП в инерциальных координатах (IF2000):

X_IF200 = AX_UGF, (19)

A = PNQ,

где P, N, Q- матрицы прецессии, нутации и учета звездного времени соответственно.

В матрице перехода от единой географической системы координат к гринвичской системе координат в качестве аргумента используется положение истинного полюса относительно ICO. Документы Международной Службы Вращения Земли, так называемые документыIERS(IERSNote) традиционно задают компоненты положения полюса как угловые величины на гринвичском меридиане и так называемую первую вертикаль, соответствующую некоторому "среднему" положению полюса. Таким образом, обобщая все вышесказанное, получаем:

X_UGF = AX_GF, (20)

A = R_x(Yp)R_y(Xp). (21)

, , (22)

где m₁иm₂- координаты истинного северного полюса Земли относительноICO.

, - средние координаты полюса.

Модель навигационных измерений.

Для каждого канала измерений НИП рассматривается следующая математическая модель:

Y(t) = G( X(t), X_TS(t), C(t) ) + (t), (23)

где Y(t) - вектор навигационных измерений (m1), гдеmможет быть числом измерений в данной модели, не превышающим 5, а именно [1]:

• наклонная дальность;

• скорость изменения наклонной дальности;

• наклонение спутника;

• прямое восхождение спутника;

• данные магнитометрической телеметрии о положении осей вращения спутника.

В формуле (23):

G( ) - вектор-функцияm1, определяющая зависимость между измеренными компонентами и компонентами расширенного вектора состояния, а также координатами НИП.

C(t) - вектор систематических ошибок измерений,m1;

(t)- вектор быстро меняющихся ошибок измерений,m1;

X(t)- вектор состояния спутника созвездия, 61;

X_TS(t)- вектор состояния НИП.

Далее, заметим, что в версии 1 Планировщика работы НИП могут быть измерены только наклонная дальность и скорость изменения наклонной дальности в случае совместного планирования по дальности и скорости изменения наклонной дальности (m:= 2) или только дальность или скорость изменения наклонной дальности в случае независимого планирования по дальности и скорости изменения наклонной дальности (m:= 1).

Для оценки вектора Cкак части расширенного вектора состояния, необходимо разработать так называемый "формирующий фильтр", который по сути, является, марковской стохастической математической моделью систематических ошибок:

(24)

где - вектор стандартного белого шума;

a- диагональная матрица коэффициентов сноса;

b- диагональная матрица коэффициентов диффузии.

Для определения введенных выше коэффициентов необходима статистическая информация о систематических ошибках; по крайней мере это должна быть информация о корреляционных функциях каждой из компонент вектора систематических ошибок. По этой причине каждый из элементов a_j, b_j(j=1m) матрицa и bзадается в виде:

(25)

где _cor- так называемый интервал корреляции; это понятие означает, что любые два значения случайного процессаc_j(j=1m) не коррелированны вне интервала_cor;

_j- априорное среднеквадратическое отклонение систематической ошибкиc_j.

Для упрощения модели положим, что r_corи , следовательно,a=b=0. Таким образом, мы получим простейшее уравнение формирующего фильтра в виде:

(26)

Начальные условия для уравнений (25) и (26) заданы:

(27)

где - априорное среднеквадратическое отклонение соответствующей систематической ошибки. Математические модели (24) или (26) определяют матрицу_S. Положим, что систематические ошибки различных измерений не коррелированны. В частности, принимая во внимание модель, заданную в (26), получим матрицу_S как единичную. В версии 1 Планировщика работы НИП используется только математическая модель (26), (27).

Случайные ошибки измерений рассматриваются как случайный процесс со следующими свойствами:

(28)

где - диагональная матрица, --функция.

Опишем соотношения, которые должны быть рассмотрены в качестве компонент вектор-функции G:

1. В первом приближении математическую модель наклонной дальности "НИП-спутник-НИП" получим без учета конечности скорости света:

(29)

где x_sc, y_sc, z_sc- координаты спутника в инерциальной системе координат;

x_ts, y_ts, z_ts- координаты НИП в инерциальной системе координат;

2. Модель скорости изменения наклонной дальности задается в виде:

(30)

где - компоненты скорости спутника в инерциальной системе координат;

- компоненты скорости НИП в инерциальной системе координат;

.

Заданные выше соотношения (29,30) используются позже для получения матрицы наблюдения H_iна основе линеаризации в окрестности опорной орбиты спутников созвездия или в окрестности орбиты, которая соответствует вектору эфемерид спутника.

Описание программы.