Построение эллипса рассеивания

Уравнение эллипса рассеивания случайной величины имеет вид:

,

где:

– коэффициент корреляции,;

– константа, соответствующая значению квантиля распределенияс двумя степенями свободы (по количеству координат) уровня доверительной вероятности, т.е.и. Значения квантилядля различного количества степеней свободы и уровней доверительной вероятности можно определить из справочника или с использованием приближенных соотношений.

Для графического отображения эллипса рассеивания можно разрешить приведенное уравнение относительно одной из координат.

8. Задачи математической статистики

(ПЗ – 2 ч, СРС – 1 ч.)

Метод Монте-Карло

Необходимый объем статистики, точность оценки

Метод статистического моделирования — универсальный метод статистического анализа стохастических систем (линейных и нелинейных, стационарных и нестационарных), подверженных воздействию случайных факторов различных типов с произвольными их статистическими свойствами. В литературе данный метод также называют методом статистических испытаний или методом Монте-Карло.

Основу метода статистического моделирования составляет закон больших чисел, заключающийся в том, что результат усреднения, относящийся к случайному фактору (событию, величине, процессу или полю), вычисленный по п его реализациям, приперестает быть случайным и может рассматриваться в качестве оценки соответствующей характеристики рассматриваемого фактора. В частности, в соответствии с теоремой . Бернулли при большом числе опытов (реализаций) частота случайного события приближается к вероятности этого события. Аналогичные теоремы существуют и для статистических характеристик случайных величин, процессов, полей.

Сущность метода статистических испытаний состоит в построении оценок статистических характеристик случайных процессов, которые допускают построение своих реализаций. Совокупность реализаций случайного процесса служит основой для построения оценки математического ожидания в момент времени:

,

где –-я реализация реализации случайного процессав момент времени,– количество реализаций, по которым строится оценка,

и оценки корреляционной матричной функции между моментами времении:

,

где справедливы все ранее введенные соотношения.

Отметим, что в этом соотношении на месте оценки предпочтительно использовать само математическое ожидание(в случае, если сведения о нем доступны).

Оценка ковариационной матрицы может быть определена, как частный случайпри.

Точность оценок

Оценки математического ожидания

и дисперсии

случайной величины , построенные на основе обработки ограниченной выборки ее реализаций,, сами являются случайными величинами.

Очевидно, что чем больше размер выборки реализаций, тем точнее несмещенная оценка, тем ближе она к истинному значению оцениваемого параметра. Ниже приведены приближенные формулы, основывающиеся на предположении об их нормальном распределении¹. Симметричный относительнодоверительный интервалдля оценки, соответствующий доверительной вероятности, определяется величиной, для которой справедливо соотношение:

,

где

– истинное значение математического ожидания случайной величины,

– среднеквадратическое отклонение случайной величины,

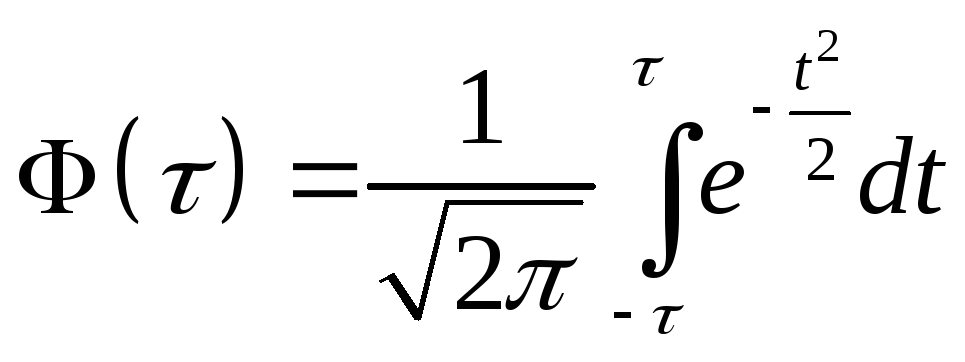– интеграл вероятностей.

На основе приведенного выше соотношения величина может быть определена следующим образом:

,

где – функция, обратная по отношению к интегралу вероятностей.

Поскольку характеристика рассеивания оценки нам в точности не известна, воспользуемся ее ориентировочным значением, вычисленным с использованием оценки:

.

Т.о. окончательное соотношение, связывающие точность оценки математического ожидания и размера выборки, по которой производится оценивание, выглядит следующим образом:

.

Это означает, что величина доверительного интервала (при неизменном значении доверительной вероятности ), расположенного симметрично относительно, выраженная в долях оценки среднеквадратического отклонения, обратно пропорциональна квадратному корню из размера выборки.

Доверительный интервал для оценки дисперсии определяется аналогичным образом:

с точностью до величины , которая за неимением более точной информации может быть приблизительно определена из соотношения:

.

Т.о. величина доверительного интервала (при неизменном значении доверительной вероятности ), расположенного симметрично относительно, выраженная в ее долях, обратно пропорциональна квадратному корню из величины, где– размер выборки.

Более точные формулы для построения доверительных интервалов²оценок могут быть получены с использованием точных сведений о законе распределения случайной величины.

Например, для гауссовского закона распределения случайная величина

подчиняется закону распределения Стъюдента с степенью свободы, а случайная величина

распределена по закону также сстепенью свободы.

Для получения достоверных оценок математического ожидания и дисперсии необходимо определить достаточный объем выборки наблюдений с использованием соотношения:

, где:

– оценка дисперсии случайной величины по предварительной выборке;

– оценка математического ожидания случайной величины по предварительной выборке;

– аргумент функции Лапласа для заданного уровня надежности:. При уровне надежности;

– относительная погрешность оценки.

Пример 1.Определить минимально необходимый объем выборки значений случайной величины для оценки её статистических характеристик с уровнем надежности 0.9 и величиной относительной погрешности не более 10%. Предварительная выборка имеет вид:

7.865; 9.826; 9.106; 8.008; 15.576; 6.454; 8.876; 9.612; 8.425; 12.692.

Определить точность предварительных оценок ,.