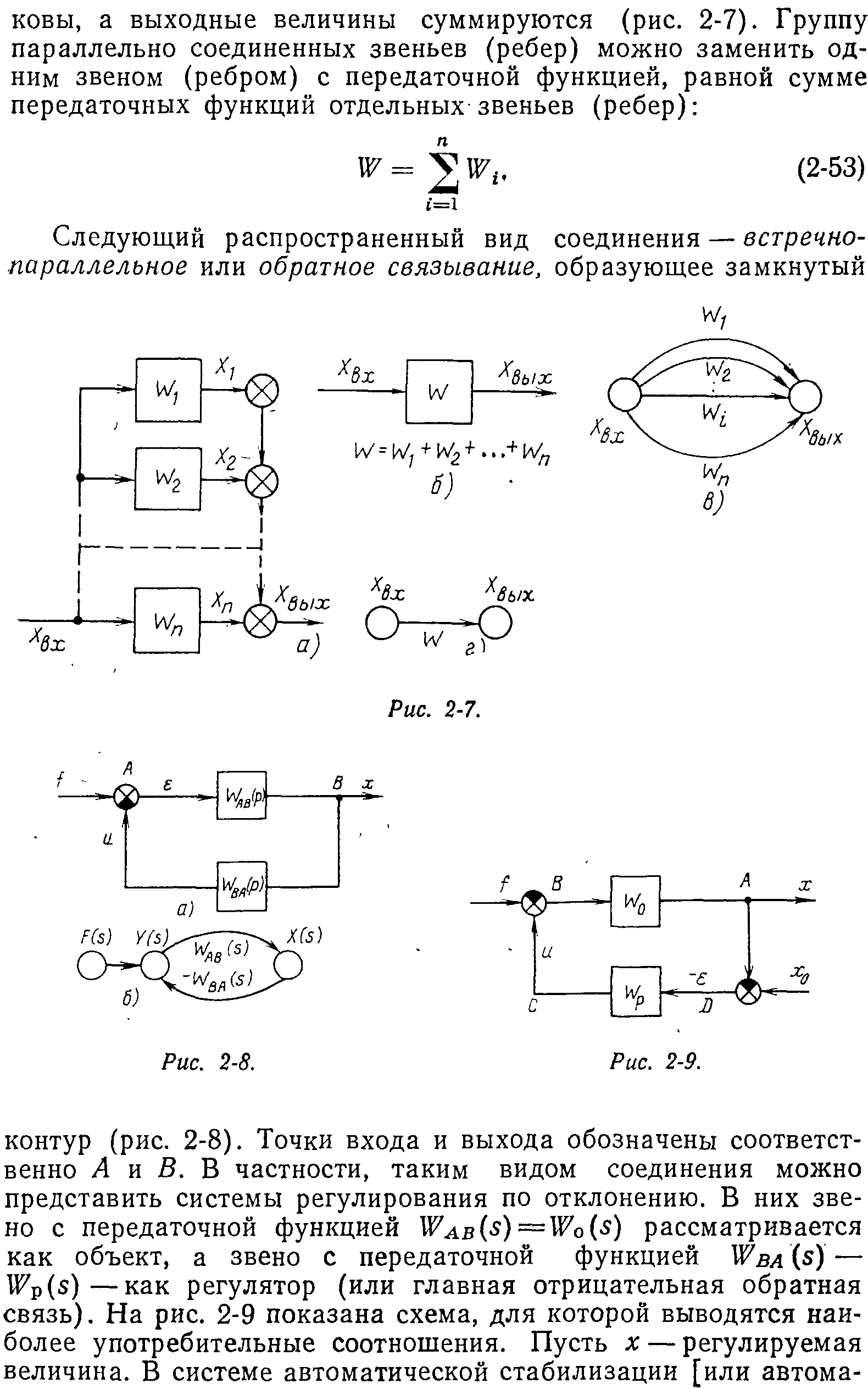
4. Задачи теории автоматического управления

(ПЗ – 2 ч, СРС – 1 ч.)

Структурные схемы динамических систем

Построение передаточных функций

Материал данного раздела излагается по монографии [1].

5. Задачи небесной механики (1)

ПЗ – 4 ч, СРС – 1 ч.

Оскулирующие элементы

Расчет координат ИСЗ на эпоху

Восстановление параметров орбиты

Материал данного раздела излагается по монографии [2].

Задачи

1. Восстановление параметров орбиты (1).Заданы вектор момента количества движения и радиус-вектор КА в апогее. Определить вектор состояния КА, находящегося на невозмущенной эллиптической орбите, на данную эпоху.

2. Восстановление параметров орбиты (2). В абсолютной геоцентрической СК заданы векторы момента количества движенияи Лапласа. Определить следующие параметры невозмущенной эллиптической орбиты:.

3. Поворот ковариационной матрицы.В инерциальных осях задана ковариационная матрица радиус-вектора цели. Угловое положение ЛА определяется значениями углов тангажа, рысканияи крена. Вычислить координаты ковариационной матрицы в связанных осях ЛА.

4. Расчет матрицы перехода.Найти матрицу перехода между СК, поворот одной из которых относительно другой определен кватернионом.

5. Переход между СК с помощью кватернионов. Определить последовательность координатных переходов между абсолютной геоцентрической СК и орбитальной СК, записать соответствующий кватернион.

6. Поворот к СК собственных осей тензора напряжений.В некоторой СК задан произвольный тензор напряжений своими координатами:

.

Построить кватернион, определяющий поворот СК к собственным осям тензора напряжений .

7. Инспекция. В абсолютной геоцентрической системе координат (СК) заданы радиус-вектори вектор скоростипервого искусственного спутника Земли (ИСЗ-1). В орбитальной СК этого ИСЗ заданы радиус-вектори вектор скоростидругого ИСЗ-2. Оба ИСЗ движутся по невозмущенным эллиптическим орбитам. Требуется построить:

а) компоненты кватерниона, определяющего переход от орбитальной СК ИСЗ-1 к орбитальной СК ИСЗ-2.

б) компоненты кватерниона, определяющего переход от геоцентрической СК к орбитальной СК ИСЗ-2.

6. Задачи небесной механики (2)

ПЗ – 2 ч, СРС – 0 ч.

Вычисление положения Луны и Солнца

Материал данного раздела излагается, главным образом, по монографии [2]

Общий алгоритм вычисления положения Луны (Солнца) может быть представлен диаграммой:

7. Задачи теории вероятностей

ПЗ – 2 ч, СРС – 0 ч.

Многомерная плотность распределения случайной величины

Построение эллипсоида рассеивания для заданного уровня доверительной вероятности

Случайные векторы

Проблема, решение которой описано в настоящем подразделе, состоит в моделировании вектора коррелированных между собой гауссовских случайных величин.

Пусть случайный вектор , подлежащий моделированию, формируется на основе преобразования вектора стандартных некоррелированных случайных величинсоответствующей размерности следующим образом:

,

где – вектор математического ожидания;– матрица коэффициентов, подлежащих определению.

Как известно, ковариационная матрица вектора , отвечающего приведенной выше зависимости, может быть определена на основе следующего соотношения:

.

Пусть матрица имеет вид:

.

Тогда, приравнивая левую и правую части уравнения поэлементно, для каждого из, например, нижнего треугольника, получим совокупностьуравнений вида:

Разрешая полученные уравнения относительно элементов матрицы , получим окончательные соотношения:

Т.о. для получения вектора коррелированных случайных величин необходимо вычислить элементы матрицы в соответствии с приведенными выше формулами и сгенерировать реализации элементов вектора гауссовских случайных некоррелированных величин, после чего воспользоваться исходным соотношением подраздела.

Нормальное распределение вероятностей n-мерного случайного вектора х описывается формулой

где — вектор математических ожиданий; — корреляционная матрица; –определитель корреляционной матрицы.

В евклидовом n-мерном пространстве, координатами которого являются составляющие вектора , плотность вероятности постоянна на концентрических гиперэллипсоидах:

называемых гиперэллипсоидами рассеивания, где С — любое поло­жительное число. Центром гиперэллипсоидов рассеивания является точка с координатами , направление главных осей совпадает с собственными векторами корреляционной матрицы , а длина каждой из главных полуосей равна , где — собственное значение корреляционной матрицы , соответствующее собственному вектору b_i.

В двумерном случае нормальное распределение (1.22) принимает вид

Плотность вероятности постоянна на эллипсах, называемых эллипсами рассеивания. Угол между главной осью эллипса рассеивания и осью Ox₁ определяется с помощью выражения

Если составляющие х₁ и х₂ вектора некоррелированы, то направления главных осей эллипса рассеивания совпадают с направлениями осей системы координат Ох₁х₂.