3. Анализ точности процесса навигационных определений ракеты-носителя с помощью инерциальной навигационной системы и радиовысотомера

Постановка задачи: Рассматривается активный участок полета ракеты-носителя (РН), оснащенной инерциальной навигационной системой и радиовысотомером. Синтезировать алгоритм оптимальной обработки измерений навигационных подсистем и с целью его анализа точности провести имитационное моделирование процесса навигационных определений с учетом неточности задания начальных условий и систематических и случайных ошибок измерений (варианты).

4. Моделирование процесса навигационных определений ракеты-носителя с помощью бескарданной инерциальной навигационной системы и многоканального приемника снс глонасс/gps.

Постановка задачи: Рассматривается активный участок полета ракеты-носителя (РН), оснащенной бескарданной инерциальной навигационной системой и многоканальным приемником СНС ГЛОНАСС/GPS. Синтезировать алгоритм оптимальной обработки измерений навигационных подсистем на основе слабосвязанной схемы комплексирования и с целью его анализа точности провести имитационное моделирование процесса навигационных определений с учетом неточности задания начальных условий, систематических и случайных ошибок измерений, а также ограничений на зону видимости антенны пользователя и на используемое число каналов (варианты).

Методические указания к заданиям №3 и №4.

1. В рамках данных заданий используются абсолютная геоцентрическая система координат (IF2000), мировая геодезическая система координат WGS-84, инерциальная навигационная СК, бортовая инерциальная СК и связанная СК. (см Приложение 1.)

2. В общем случае, полный вектор состояния РН задается компонентами положения и скорости в инерциальной навигационной СК, а также углами Эйлера или матрицей перехода от инерциальной навигационной СК к связанной, характеризующие угловой положение РН на активном участке полета. При этом предполагается, что начальный вектор состояния является случайным, распределенным по нормальному закону с заданным вектором математического ожидания и ковариационной матрицей.

3. Для моделирования «истинного» движения РН используется файл, содержащий компоненты положения, полной скорости и кажущейся скорости в инерциальной навигационной СК, а также углы Эйлера заданные с шагом 1с. на всем протяжении активного участка полета РН. Таким образом, для использования данной информации при моделировании процесса навигационных определений необходимо использовать аппроксимацию вышеупомянутых данных каким-либо методом полиномиальной аппроксимации. В качестве начальных условий для опорной (навигационной) траектории РН информация из файла в момент старта РН используется как вектор математического ожидания.

4. (Только для задания №3) Источником данных для бортовой инерциальной навигационной системы является информация поступающая с бортового измерительного комплекса (БИК). Основными компонентами БИК являются гиростабилизированная платформа и блок интегрирующих акселерометров.

Гиростабилизированная платформа представляет собой три двухстепенных гироскопа, расположенных в трех взаимно перпендикулярных плоскостях, и предназначена для создания на борту ЛА бортовой навигационной системы координат. Однако, в действительности, моделируемая гиростабилизированной платформой система координат отличается от ИНСК вследствие следующих причин:

• Начальная выставка гиростабилизированной платформы на стартовой позиции осуществляется неидеально, иными словами, оси моделируемой системы координат (данную систему координат будем обозначать далее как НСК1)отличаются от ИНСК на ошибки начальной выставки ГСП. Данное отличие описывается последовательностью трех поворотов на углы, соответствующие ошибкам начальной выставки, и преобразование координат в этом случае описывается матрицей поворота, вычисляемой по следующей методике:

где -координаты объекта в инерциальной навигационной системе координат,

-координаты объекта в навигационной системе координат 1,

- матрица преобразования ИНСК в НСК1,

,

где

A - угол поворота ИНСК, соответствующий ошибке выставки азимута:

,

H - угол поворота ИНСК, соответствующий ошибке выставки горизонта:

,

V - угол поворота ИНСК, соответствующий ошибке выставки вертикали:

,

• С течением времени полета ориентация гироплатформы будет все больше отличаться от начального. Источником ошибок в ориентации ГСП помимо не идеальности начальной выставки, является прецессия гироскопов, зависящая от времени полета ЛА и от перегрузок, возникающих в течении полета, и приводящая к . Уход гиростабилизированной платформы, вызванных угловым дрейфом можно описать при помощи следующей матрицы:

где , - суммарная погрешность ориентации осей ГСП в проекции на оси ИНСК.

Динамика дрейфа описывается следующим образом:

где ,- суммарная погрешность на i+1 и i моменты времени соответственно,

- суммарный уход осей ГСП за промежуток времени .

В свою очередь можно представить как сумму “свободного” ухода ГСП, не зависящего от внешних воздействий, а зависящего только от времени, и погрешность в ориентации осей вызванная действием перегрузок:

где - вектор скорости “свободного” ухода осей ГСП,

,

где - вектор скорости ухода осей, пропорциональный ускорению;

- вектор скорости ухода осей ГСП из-за ошибок дисбаланса при действии ускорения в направлении кинетических моментов;

- вектор скорости ухода осей ГСП из-за ошибок неравножесткости.

Компоненты векторов скорости ухода осей являются гауссовскими случайными величинами.

• Измерения приращений кажущейся скорости проводятся с помощью интегрирующих акселерометров. Интегрирующие акселерометры представляют собой тяжелый двухстепенной гироскоп, тело которого закреплено на протяженной штанге. Они расположены по трем взаимно перпендикулярным осям, совпадающим с осями ГСП. Блок акселерометров, так же как и гироплатформа, имеет ошибки начальной выставки. Моделирование данных ошибок производится по схеме, аналогичной схеме моделирования ошибок начальной выставки ГСП и соответствующая матрица , описывающая преобразование от системы координат НСК2 к БНСК выглядит следующим образом:

,

где X, Y, Z - углы, соответствующие ошибкам ориентации блока акселерометров:

,

,

,

• Кроме того, коэффициент усиления каждого акселерометра является гауссовской случайной величиной с характеристиками:

• Помимо этого, измерения каждого акселерометра сопровождаются случайной ошибкой измерений, являющейся гауссовской величиной с характеристиками:

,

Тогда, полный алгоритм моделирования работы БИК, т.е. процесс формирования измерений приращений кажущейся скорости, снимаемых с акселерометров, можно представить в следующем виде:

1. Пусть вектор реальных приращений кажущейся скорости W_ИНСК. Тогда осуществляя преобразование ИНСК к БНСК получаем значение вектора приращений кажущейся скорости в БНСК:

W_БНСК = R_aD_ГСПR_НВW_ИНСК.

2. Значения вектора приращение кажущейся скорости, снимаемых с акселерометров вычисляются в соответствии со следующим соотношением:

где W = (W_x, W_y, W_z)^T - вектор случайных ошибок измерений;

S_x, S_y, S_z - значения коэффициентов усиления акселерометров.

Кроме того, акселерометры обладают зоной нечувствительности, в связи с чем приращение кажущейся скорости поступающее с акселерометров сравнивается с некоторым пороговым значением. Если величина меньше порога, то на выход передается 0.

5. Упрощенная модель функционирования БИК описывается следующими соотношениями:

где:

- вектор приращений кажущейся скорости за такт работы ИНС, измеренный блоком акселерометров;

- вектор приращений кажущейся скорости за такт работы ИНС на истинной траектории РН;

- вектор случайных аддитивных ошибок измерений акселерометров;

- вектор систематических ошибок измерений акселерометров, обусловленный ошибками начальной выставки; является постоянным в течение всего активного участка и задается начальным разбросом с ;

- вектор систематических ошибок измерений акселерометров, обусловленный угловым дрейфом гироскопов; формируется в соответствии со следующей моделью:

,

т.е. включает дрейф, пропорциональный времени полета, действующим ускорениям и квадрату действующего ускорения;

- вектор систематических ошибок измерений акселерометров, обусловленный ошибками ориентации гироблоков; является постоянным в течение всего активного участка и задается начальным разбросом с ;

6. (Только для задания №3) Алгоритм работы бортовой инерциальной навигационной системы основан на интегрировании поступающих от интегрирующих акселерометров значений приращений кажущихся скоростей РН и восстановлении по вычисленному кажущемуся пути полного положения и скорости РН в инерциальной навигационной системе координат, посредством учета ускорений, вызванных гравитационным влиянием Земли. ИНС начинает свою работу за несколько секунд до старта и заканчивает после выгорания последней ступени (конец активного участка). Навигационная задача решается на борту один раз в секунду. БИК работает на частоте 64 Гц, т.е. БИК успевает сделать 64 измерения приращений кажущейся скорости. Эту информацию в течение секунды накапливает бортовой компьютер (БК).

Алгоритм работы ИНС формализуется следующими соотношениями:

где:

X_ИНСК – оценка компонент положения РН в ИНСК;

V_ИНСК – оценка компонент скорости РН в ИНСК;

- измеренная кажущаяся скорость РН до i-1 такта работы ИНС;

g(X_GR) – ускорение, обусловленное силой притяжения Земли.

Алгоритм вычисления проекции гравитационного поля силы притяжения Земли записывается в следующем виде:

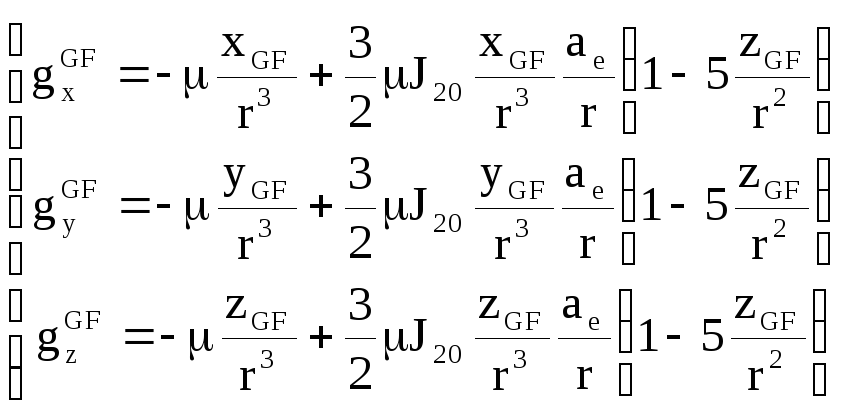
где

 - константа гравитационного поля Земли (398600,44 км³/с²);

a_e – экваториальный радиус Земли (6378,136 км);

J₂₀ – коэффициент при второй зональной гармонике (-1082.63*10^-6).

Необходимо отметить, что для вычисления данных ускорений требуется пересчитать положение РН в гринвичскую СК, а после вычисления ускорений перевести полученные значения в инерциальную навигационную СК (см. Приложение №1).

6. (Только для задания №3) Моделирование работы радиовысотомера осуществляется в соответствии со следующим алгоритмом:

,

где

h_РВ– высота полета над поверхностью, измеренная радиовысотомером;

h^tr– истинная высота полета вертолета;

h_РВ– ошибки измерения высоты, определенные следующим образом:

,

где

- систематическая ошибка измерения высоты РВ, представляющая собой нормально распределенную случайную величину с нулевым математическим ожиданием и заданным уровнем СКО ;

- динамическая составляющая ошибки измерения высоты, представляющая собой стационарный случайный процесс, воспроизводимый стохастическим дифференциальным уравнением вида:

где - постоянная времени привода РВ,

- переменный коэффициент усиления фильтра, зависящий от разности истинной высоты , оценки высоты ИНС, разности истинного и измеренного значения крена (), а также истинного и измеренного значения тангажа (),

w - стандартный белый шум с единичной интенсивностью,

- случайная аддитивная составляющая ошибки измерения высоты, представляющая собой стационарный случайный процесс с нулевым математическим ожиданием и корреляционной функцией вида:

где - среднеквадратическое отклонение (СКО)от среднего значения;- коэффициент затухания корреляционной функции для случайной ошибки измерения высоты.

Как известно, стохастическое дифференциальное уравнение формирующего фильтра, воспроизводящего случайный стационарный процесс с такой корреляционной функцией имеет вид:

,

где w- стандартный белый шум с единичной интенсивностью.

7. Алгоритм оптимальной фильтрации представляет собой квазилинейный фильтр Калмана для фиктивной динамической системы, модель движения которой включает вышеприведенные уравнения инерциальной навигации, дифференциальные уравнения ошибок ориентации и формальные дифференциальные уравнения для систематических ошибок гироскопов и акселерометров, а в качестве измерений – измерения радиовысотомера.

8. (Только для задания №4)Моделирование работы резервного навигационного контура СНС сводится к следующему алгоритму:

где

- оценка положения и скорости РН в гринвичской СК, вычисленная многоканальным приемником ГЛОНАСС/GPS;

- «истинные» положение и скорость РН в гринвичской СК (из файла с траекторией);

- ошибка определения положения и скорости РН в гринвичской СК:

,

- систематическая ошибка определения координат и скоростей РН;

аддитивная ошибка определения координат и скоростей РН, представляет собой реализацию случайного процесса, определяемого следующим уравнением формирующего фильтра первого порядка:

где

w – белый шум;

_и _ – интервал корреляции и с.к.о. данного случайного процесса.

9. (Только для задания №4). Для функционирования бескарданной ИНС (БИНС) предусмотрен собственный измерительный комплекс, содержащий блок акселерометров, измеряющий вектор кажущегося ускорения в связанной СК, и блок датчиков угловой скорости, измеряющий вектор абсолютной угловой скорости ЛА в связанной СК.

Модель измерений акселерометров.

Измерения каждого из трех акселерометров, установленных по осям связанной СК формируются следующим образом:

,

где

- реальное («истинное») значение кажущегося ускорения вдоль i^ой оси связанной СК;

N_i – погрешность акселерометра, определяемая следующим образом:

,

где

- систематическая погрешность акселерометра, представляющая собой случайную величину, распределенную по нормальному закону;

- коэффициенты, учитывающие влияние величины ускорения на результат измерений; как правило постоянные величины, указываемые производителем акселерометров, однако, могут быть оценены в дальнейшем;

N_i – случайная аддитивная ошибка измерений акселерометров, представляющая собой реализацию случайного процесса, определяемого следующим уравнением формирующего фильтра первого порядка:

где

w – белый шум;

_N и _N – интервал корреляции и с.к.о. данного случайного процесса.

Модель измерений датчиков угловой скорости.

Измерения каждого из трех датчиков угловой скорости, установленных по осям связанной СК формируются следующим образом:

,

где

- реальное («истинное») значение проекции абсолютной угловой скорости ЛА на i^ую ось связанной СК;

_i – погрешность датчика угловой скорости, определяемая следующим образом:

,

где

- систематическая погрешность датчика угловой скорости, представляющая собой случайную величину, распределенную по нормальному закону;

- коэффициенты, учитывающие влияние величины угловой скорости на результат измерений; как правило постоянные величины, указываемые производителем ДУС, однако, могут быть оценены в дальнейшем;

- коэффициенты, учитывающие влияние величины ускорения на результат измерений; как правило постоянные величины, указываемые производителем ДУС, однако, могут быть оценены в дальнейшем;

_i – случайная аддитивная ошибка измерений датчика угловой скорости, представляющая собой реализацию случайного процесса, определяемого следующим уравнением формирующего фильтра первого порядка:

где

w – белый шум;

_и _ – интервал корреляции и с.к.о. данного случайного процесса.

10. (Только для задания №4). Необходимо отметить, что навигационное решение, формируемое БИНС, является основным, т.е. в различных условиях полета и при различном состоянии глобальных навигационных систем именно навигационные определения БИНС позволяют сохранить относительную автономность системы, обеспечивая в тоже время приемлемую точность решения целевой задачи. Алгоритм работы БИНС состоит из двух частей:

• алгоритм определения положения и скорости КА;

• алгоритм определения ориентации ЛА.

Алгоритм определения положения и скорости РН.

Алгоритм работы определения положения и скорости РН основан на интегрировании поступающих от интегрирующих акселерометров значений кажущихся ускорений РН и восстановлении по вычисленному кажущемуся пути полного положения и скорости РН в инерциальной навигационной системе координат, посредством учета ускорений, вызванных гравитационным влиянием Земли. БИНС начинает свою работу за несколько секунд до старта и заканчивает после выгорания последней ступени (конец активного участка). Навигационная задача решается на борту с частотой 10 Гц.

Алгоритм работы ИНС формализуется следующими соотношениями:

где:

X_ИНСК – оценка компонент положения РН в ИНСК;

V_ИНСК – оценка компонент скорости РН в ИНСК;

g(X_GR) – ускорение, обусловленное силой притяжения Земли.

- измеренные акселерометрами кажущиеся ускорения РН в ИНСК.

Алгоритм вычисления проекции гравитационного поля силы притяжения Земли записывается в следующем виде:

где

 - константа гравитационного поля Земли (398600,44 км³/с²);

a_e – экваториальный радиус Земли (6378,136 км);

J₂₀ – коэффициент при второй зональной гармонике (-1082.63*10^-6).

Необходимо отметить, что для вычисления данных ускорений требуется пересчитать положение РН в гринвичскую СК, а после вычисления ускорений перевести полученные значения в инерциальную навигационную СК (см. Приложение №1).

Кажущиеся ускорения РН в ИНСК связаны с вектором кажущегося ускорения, измеряемого акселерометрами БИНС следующим соотношением:

,

где A^БИНС- матрица перехода между географической и связанной СК, вычисляемая в алгоритме определения ориентации ЛА (см. ниже);

- вектор кажущегося ускорения ЛА в связанной СК, измеряемый акселерометрами БИНС.

Алгоритм определения ориентации РН.

Для вычисления углов ориентации РН используется подход, основанный на интегрировании дифференциальных уравнений для матрицы перехода между связанной и инерциальной навигационной СК (матрицы Пуассона):

c начальными условиями .

Для определения начальных условий (матрицы ) используется начальная выставка БИНС на Земле или в процессе полета носителя. Выставка осуществляется методом векторного согласования по измерениям двух неколлинеарных векторов измерительными элементами БИНС (акселерометрами, гироскопами) вектора абсолютной угловой скорости вращения ЛА, равного угловой скорости вращения Земли u, и вектора ускорения свободного падения g.

_1,2,3 - абсолютные угловые скорости ЛА измеряемые гироскопами БИНС.

Тогда Эйлеровы углы ориентации ЛА определяются следующим образом:

.

Второй подход при построении алгоритма ориентации базируется на использовании промежуточных параметров ориентации. При создании БИНС наиболее часто в качестве них используются параметры Родрига-Гамильтона. Матрица пересчета из связанной в базовую систему координат реализуется в параметрах Родрига-Гамильтона, которые, в свою очередь, вычисляются численным алгоритмом второго порядка, построенном на основе метода последовательных приближений Пикара:

_^_^________

A^БИНС_____^_^____

_________^_^

_^{}_^_^_^__^__^_

_^{}_^_^_^__^__^_

_^{}_^_^_^__^__^_

_^{}_^_^_^__^__^_



где_^_^_^

____приращения интегралов от проекций абсолютной угловой скорости поворота на оси чувствительности гироскопов (например, показания лазерных гироскопов).

11. Алгоритм комплексирования (АК) на основе слабосвязанной схемы заключается в определении поправок оценок положения РН посредством обработки измерений, в качестве которых выступают оценки положения и скорости РН, сформированные многоканальным приемником ГЛОНАСС/GPS. Модель движения динамической системы представляет собой уравнения ошибок ИНС, дополненные формальными дифференциальными уравнениями для систематических ошибок чувствительных элементов.

Необходимо отметить, что оценка положения и скорости РН, полученная многоканальным приемником СНС определена в гринвичской СК и для дальнейшего ее использования в ИНС необходимо осуществить преобразование из ГСК в ИНСК.

12. Для моделирования работы контуров ИНС и БИНС необходимо использовать численный метод интегрирования класса прогноз-коррекция, обеспечивающий эффективные вычисления и устойчивость численного решения уравнений с заданным уровнем локальной ошибки.

Данный метод относится к группе методов Адамса-Мултона-Башфорда. Рассмотрим реализацию этого метода в рамках одного шага интегрирования векторного обыкновенного дифференциального уравнения первого порядка:

,

где

h - шаг интегрирования;

t - переменная интегрирования;

y₀ - начальное условие.

Суть метода состоит в первоначальном прогнозе численного решения методом Эйлера (явный метод Адамса) с последующей коррекцией методом трапеций (неявный метод Адамса) до сходимости либо по достижению заданного количества итераций:

1. - прогноз;

2. - вычисления правых частей диф. уравнений в конце шага;

3. - коррекция;

4. - вычисления правых частей диф. уравнений в конце шага.

Этапы 3 и 4 повторяются до тех пор, пока не будет выполнено условие

или kk^*,

где

W – весовая матрица системы дифференциальных уравнений;

k – номер итерации;

k* - максимальное количество итераций;

tol – заданная локальная погрешность интегрирования.

Используемый метод интегрирования позволяет добиться получения высокоточного, устойчивого численного решения с постоянным шагом интегрирования. Кроме того, вследствие использования формулы коррекции, зависящей от правых частей диф. уравнений в конце шага интегрирования, данный метод не вносит запаздывания численного решения при обработке измерений за шаг интегрирования.