Федеральное агентство по образованию

МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

ФАКУЛЬТЕТ №7 «РОБОТЕХНИЧЕСКИЕ И ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ»

кафедра «Информационно-управляющие комплексы» (704)

Утверждено на заседании метод.совета факультета №7

сентября 2007 г.

протокол №7

К.И.Сыпало

Варианты заданий и методические указания по выполнению КУРСОВЫХ работ по дисциплине

Комплексирование информационных приборов

для специальности 131600

Обсуждено на заседании кафедры №704

сентября 2007 г.

протокол №

Москва, 2007

СОДЕРЖАНИЕ

1. Анализ точности процесса навигационных определений неподвижного потребителя с помощью многоканального приемника СНС ГЛОНАСС/GPS. 3

2. Анализ точности процесса навигационных определений ИСЗ с помощью многоканального приемника СНС ГЛОНАСС/GPS. 3

3. Анализ точности процесса навигационных определений ракеты-носителя с помощью инерциальной навигационной системы и радиовысотомера 12

4. Моделирование процесса навигационных определений ракеты-носителя с помощью бескарданной инерциальной навигационной системы и многоканального приемника СНС ГЛОНАСС/GPS. 13

5. Моделирование работы комплексированной навигационной системы подвижного объекта на основе совместного использования радиобаровысотомера и многоканального приемника СНС ГЛОНАСС/GPS. 32

1. Анализ точности процесса навигационных определений неподвижного потребителя с помощью многоканального приемника СНС ГЛОНАСС/GPS.

Постановка задачи: Потребитель (пользователь) СНС находится неподвижно в точке, определяемой координатами на поверхности общего земного эллипсоида (r, , ) и оснащен многоканальным приемником СНС ГЛОНАСС/GPS. С целью анализа точности необходимо провести имитационное моделирование процесса навигационных определений непосредственным решением навигационных определений либо методом наименьших квадратов по полной выборке измерений псевдодальности до навигационных ИСЗ СНС с учетом неточности задания начальных условий, систематических и случайных ошибок измерений, а также ограничений на зону видимости антенны пользователя и на используемое число каналов (варианты).

2. Анализ точности процесса навигационных определений исз с помощью многоканального приемника снс глонасс/gps.

Постановка задачи: ИСЗ (пользователь СНС) движется по круговой орбите с заданными параметрами орбиты и оснащен многоканальным приемником СНС ГЛОНАСС/GPS. С целью анализа точности необходимо провести имитационное моделирование процесса навигационных определений методом наименьших квадратов по полной выборке (рекуррентным байесовским фильтром) измерений псевдодальности и псевдоскорости до навигационных ИСЗ СНС с учетом неточности задания начальных условий, систематических и случайных ошибок измерений, а также ограничений на зону видимости антенны пользователя и на используемое число каналов (варианты).

Методические указания к заданиям №1 и №2.

0. В рамках данных заданий используются абсолютная геоцентрическая система координат (IF2000) и мировая геодезическая система координат WGS-84. (см Приложение 1.)

1. В общем случае, полный вектор состояния пользователя СНС задается компонентами положения и скорости в одной из систем координат, указанной в п.0. При этом предполагается, что начальный вектор состояния является случайным, распределенным по нормальному закону с заданным вектором математического ожидания и ковариационной матрицей.

2. Для моделирования движения навигационных ИСЗ СНС ГЛОНАСС/GPS используется простейшая модель движения КА в центральном поле Земли на основе интегрирования методом Эйлера уравнений вида:

(1.1)

где x,y,z - координаты центра масс спутника в IF 2000,

- радиус-вектор спутника,

- гравитационная постоянная Земли.

При моделировании «истинного» и опорного движения НИСЗ используются различные начальные условия движения НИСЗ: для опорного движения используются детерминированные значения н.у., а для «истинного» н.у. являются случайными, распределенными по нормальному закону с заданным математическим ожиданием и ковариационной матрицей.

3. (Только для задания №2)

При моделировании «истинного» движения КА (пользователя СНС) используется модель движения, идентичная приведенной выше со случайными начальными условиями распределенными по нормальному закону с заданным математическим ожиданием и ковариационной матрицей. Для моделирования опорной орбиты КА используется линеаризованная в окрестности опорной круговой орбиты траектория:

(1.2)

где x_i - отклонение вектора состояния от номинального значения в момент времени t_i.

Фундаментальная матрица Ф_i,i-1 задана в виде:

,

где t_i-1 - начальный момент времени,

t_{i -} конечный момент времени,

I - единичная матрица 66,

A(t) - матрица линеаризованной системы (1.1):

(1.3.)

4. Модель измерений «истинной» псевдодальности до НИСЗ описывается следующими соотношениями:

,

где

- “истинное” значение дальности между антенной потребителя и НИСЗ;

- “истинный” радиус-вектор НИСЗ;

- “истинный” радиус-вектор антенны;

- систематическая ошибка, вызванная разностью временных шкал НИСЗ и приемника и ионосферной задержкой сигнала; представляет собой случайную центрированную гауссовскую величину с заданной дисперсией;

- случайная аддитивная ошибка, обусловленная внутренними шумами приемника, представляющая собой реализацию случайного процесса, определяемого следующим уравнением формирующего фильтра первого порядка:

где

w – белый шум;

_и _ – интервал корреляции и с.к.о. данного случайного процесса.

Модель измерений «опорной» псевдодальности до НИСЗ описывается следующими соотношениями:

,

где

- опорное значение дальности между антенной потребителя и НИСЗ;

- опорный радиус-вектор НИСЗ;

- опорный радиус-вектор антенны.

Модель измерений «истинной» производной дальности до НИСЗ описывается следующими соотношениями:

,

где

- “истинное” значение производной дальности между антенной потребителя и НИСЗ;

- “истинное” значение вектора скорости НИСЗ;

- “истинное” значение вектора скорости антенны;

- единичный вектор в направлении “истинной” дальности между антенной и НИСЗ;

- систематическая ошибка измерений производной дальности; представляет собой случайную центрированную гауссовскую величину с заданной дисперсией;

- случайная аддитивная ошибка, обусловленная внутренними шумами приемника представляющая собой реализацию случайного процесса, определяемого следующим уравнением формирующего фильтра первого порядка:

где

w – белый шум;

_и _ – интервал корреляции и с.к.о. данного случайного процесса.

Модель измерений «опорной» производной дальности до НИСЗ описывается следующими соотношениями:

,

где

- опорное значение производной дальности между антенной пользователя и НИСЗ;

- опорное значение вектора скорости НИСЗ;

- опорное значение вектора скорости антенны;

- единичный вектор в направлении опорной дальности между антенной и НИСЗ

Рис. 1.1.

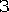
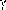
5. Среди полного созвездия НИСЗ необходимо учитывать только видимые, т.е. находящиеся в непосредственной геометрической видимости (см. рис. 1.1.)

Условие проверки видимости формируется следующим образом:

Для того чтобы выяснить будет ли НИСЗ находиться в зоне видимости потребителя, необходимо сравнить , угол  должен быть больше чем угол  (см. рис. 1.1).

6. Метод непосредственного решения навигационной задачи (только для задания №1) относится к конечным и состоит в следующем:

В результате навигационного сеанса известны координаты НИСЗ и измеренные значения дальностей до НИСЗ. Дальность выражается через координаты потребителя и НИСЗ следующим образом:

i=1,2,3.

где - значение дальности до i-го НИСЗ,

- прямоугольные координаты i-го НИСЗ,

-прямоугольные координаты потребителя.

Решая совместно эти уравнения и проведя ряд замен переменных получаем в итоге квадратное уравнение относительно z:

где ,

,

,

,

,

,

.

Решение квадратного уравнения дает оценку координаты z. Значения координат x и y вычисляются подстановкой z с систему уравнений x(z),y(z):

.

Двузначность, связанная с решением квадратного уравнения решается путем сравнения со счисляемым местом.

Итерационные методы решения системы нелинейных уравнений различаются объемом и скоростью сходимости. Среди итерационных методов по выборке минимального объема наибольшее распространение имеет метод Ньютона, как один из проще всего реализуемых и быстро сходящихся. В качестве априорной информации требуются координаты потребителя. По окончании навигационного сеанса известны координаты НИСЗ i=1,2,3 , дальности до НИСЗ . Далее рассчитываются невязки, которые рассчитывают путем вычитания расчетных величин из измеренных :

где

Решение системы методом Ньютона представляет собой процесс многократной обработки результатов навигационных измерений. В векторном виде решение можно представить следующей формулой:

где - вектор оцениваемых параметров объекта,

- вектор невязок,

- матрица наблюдения, ,

где , ,

Таковы конечный и итерационный методы навигационных определений по минимально необходимому объему. Если при решении навигационной задачи есть возможность получить избыточный объем измерений, то целесообразно пользоваться статистическими методами обработки выборки измерений.

6. Для нахождения вектора состояния применяется метод наименьших квадратов (МНК) по полной выборке (только для задания №1). Минимизация функции квадратов невязок,

где - невязка i-го измерения,

- вес i-го измерения, _i=²₀/²_i ,

лежит в основе оценивания искомых параметров по методу МНК. Невязка представляет собой разность между измеренной и расчетной величинами. Навигационной функцией в данном случае является дальность измеренная в ходе навигационного сеанса:

.

Так как функция является нелинейной, а МНК применим для линейных функций. линеаризуем ее разложением в ряд Тейлора в окрестности опорного положения:

.

Преобразуя полученное выражение, получим уравнение для приращения навигационной функции:

где

Приращение оценки в матричной форме записывается в следующем виде :

,

где W представляет из себя матрицу весов измерений, размерностью :

В результате вычислений получим значение оценки приращения положения потребителя. Затем сравним ее с заданной точностью вычислений, если полученная оценка не удовлетворяет заданной точности, то совершается новая итерация по ее улучшению. В противном случае, проводится новый сеанс измерений.

Таким образом, при использовании данного алгоритма используется линеаризованная в окрестности опорного положения потребителя модель измерений. Это означает, что начальное приближение координат должно незначительно отличаться от истинного, так как в противоположном случае линеаризация измерений некорректна и гарантировать сходимость вышеуказанного алгоритма не представляется возможным.

6. При обработке измерений рекуррентным байесовским алгоритмом (фильтром Калмана) используется линеаризованная модель движения 1.2 с фундаментальной матрицей решения 1.3. и моделью измерительных каналов, изложенных в п.4.

Уравнение фильтра запишем в виде:

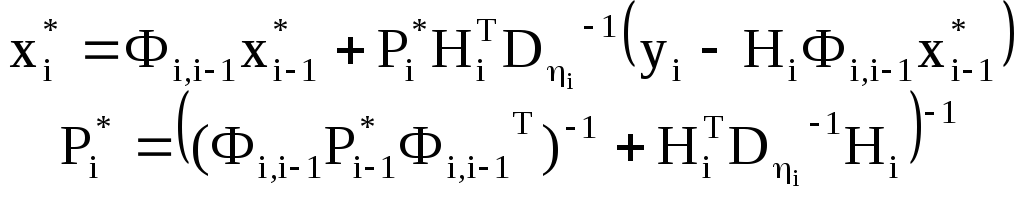
где - апостериорная оценка отклонения вектора состояния КА от опорного значения;

y_i – вектор истинных измеренных параметров (дальность и производная дальности);

H_i – матрица частных производных измеренных параметров по вектору состояния КА в окрестности опорной траектории;

D_i – матрица интенсивностей шумов измерений.

Необходимо отметить, что также как и в предыдущем случае(п.7), в алгоритме вычисляются отклонения положения и скорости КА от опорных значений.

6. В случае уточнения систематических ошибок измерений дальности и производной дальности необходимо внести данные компоненты в расширенный фазовый вектор системы с формальных дифференциальным уравнением

и произвести их оценку учитывая изменения в фундаментальной матрице и матрице измерений.