Метод непосредственных навигационных определений

Метод непосредственного решения навигационной задачи относится к конечным и состоит в следующем. В результате навигационного сеанса известны координаты НИСЗ и измеренные значения дальностей до НИСЗ. Дальность выражается через координаты потребителя и НИСЗ следующим образом:

,,

где - значение дальности до-го НИСЗ,

– координаты-го НИСЗ в инерциальной геоцентрической СК;

– координаты потребителя. в инерциальной геоцентрической СК.

Решая совместно уравнения для трех НИСЗ и проведя ряд замен переменных можно получить квадратное уравнение относительно координаты :

, где:

;

;

;

;

;

;

.

Решение квадратного уравнения дает оценку координаты . Значения координативычисляются подстановкойс систему уравнений,:

.

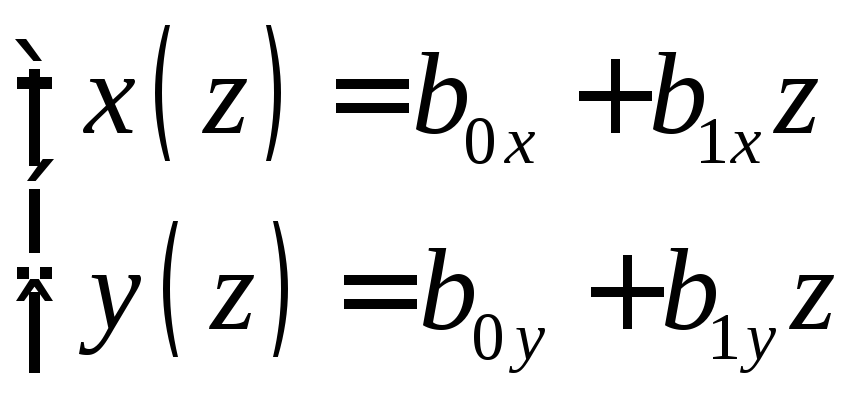Двузначность, связанная с решением квадратного уравнения решается путем сравнения со счисляемым местом.

После определения координат пользователя в инерциальной геоцентрической СК их необходимо перевести в геодезическую СК. На основании полученных значений строится оценка математического ожидания, ковариационной матрицы и эллипс рассеивания координат точки местонахождения потребителя.

Оценивание математического ожидания и ковариационной матрицы координат точки местонахождения потребителя

В процессе навигационного сеанса требуется уточнять оценки математического ожидания и ковариационной матрицы координат точки местонахождения потребителя по нарастающей выборке с использованием следующих рекуррентных соотношений метода Монте-Карло [1, 5]:

, где

– вектор координат точки местонахождения потребителя в геодезической СК рассчитанный в результате проведения-го навигационного определения;

– оценка математического ожидания вектора координат точки местонахождения потребителя, построенная после проведения-го навигационного определения.

, где

– оценка ковариационной матрицы оценки координат точки местонахождения потребителя.

Следует отметить, что оценка математического ожидания и ковариационной матрицы могут производиться и традиционным способом – по полной выборке.

Построение эллипса рассеивания координат точки местонахождения потребителя

Для получения представления об области возможного местонахождения потребителя с заданной вероятностью удобно использовать эллипс рассеивания (будем рассматривать область местонахождения потребителя в местной горизонтальной плоскости, т.е. не учитывая высоту над общим земным эллипсоидом). Эллипс рассеивания строится по завершении навигационного сеанса и получении окончательных оценок широты и долготы точки местонахождения потребителя.

Уравнение эллипса имеет вид:

,

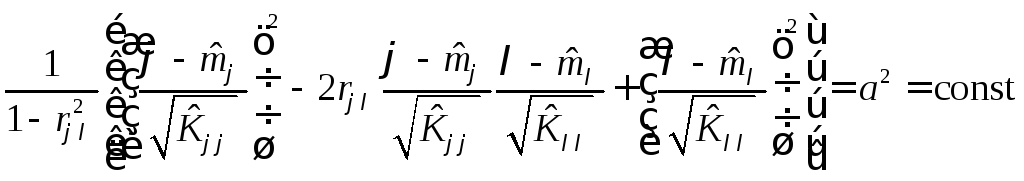где:

– коэффициент корреляции,;

– константа, соответствующая значению квантиля распределенияс двумя степенями свободы (по количеству координат) уровня доверительной вероятности, т.е.и[1, 2, 8]. Значения квантилядля различного количества степеней свободы и уровней доверительной вероятности можно определить из справочника или с использованием приближенных соотношений [1, 2, 8].

Для графического отображения эллипса рассеивания можно разрешить приведенное уравнение относительно одной из координат.

Оформление работы и представление результатов

Рекомендованное оформление работы подробно рассмотрено в [5]. Работа может включать следующие разделы: постановка задачи, математические модели, алгоритмы, численные методы, вычислительные эксперименты и их результаты (с указанием сценариев экспериментов), выводы.

Основными результатами курсовой работы являются графики эволюции координат НИСЗ орбитальной группировки на протяжении навигационного сеанса, численные значения оценок математического ожидания и ковариационной матрицы оценок координат точки местоположения потребителя, а также графическое отображение эллипса рассеивания в местной горизонтальной плоскости. При использовании рекуррентных соотношений для построения этих оценок необходимо отобразить графики их эволюции в течение навигационного сеанса.

Представляет интерес анализ зависимости точности решения навигационной задачи от точности измерений (на графиках можно показать зависимости ).