Tr_ma4s

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

+ (y + 1)2

(x − 1) + (y + 1) > 1

Первое неравенство системы представляет собой множество-

.pdf

Скачиваний:

Добавлен:

10.05.2015

Размер:

716.58 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Используя определение модуля (1.2), получим

(x − 1)2 + (y + 1)2 ≤ 2

(x − 1)2 + (y + 1)2 > 1,

возводя в квадрат, получим

внутри круга с центром в точке 1 − i и радиусомВМR2 = 2. Граница области входит в рассматриваемое множество. Второе неравенство системы – это внешность единичного круга с центром в точке 1−i, граница круга в область не входит. Одновременное выполнение двух неравенств определяет кольцо с центром в точке z0 = 1 − i и

радиусами R1 = 1, r2 = 2. Т.к. окружность радиуса R1					не входит
в область, ее обозначают пунктиром (см. рис.8)МИРЭА.
Пример 1.15.
	π		π
−		< arg z ≤		.
	6		3
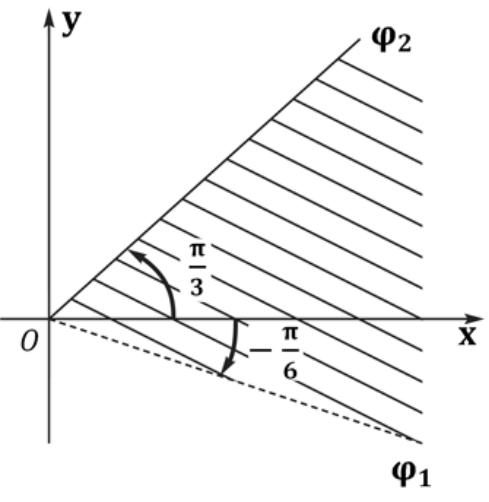
Решение: множество точек, удовлетворяющих двойному нера-
		Кафедра


венству, совпадает с точками угла с вершиной в начале координат,
заключенного междуМГТУлучами ϕ1 = − 6 и ϕ2 = 3 . Луч ϕ2 =					3 вхо-
	π			π	π
дит в данное множество, а луч ϕ1 = −		π	– не входит (см. рис.9).

		6

Пример 1.16.

МИРЭА

Кафедра(x − 1) + y ≥ (x + 1)

+ y

Рис.9

z − 1

≥

МГТУ

z + 1

Решение: умножим обе части неравенства на положительное

число z + 1 , получим z

z + 1 . Положим z = x + iy.

−

| ≥ | |

Возведем в

квадрат:

(x − 1)2 + y2 ≥ (x + 1)2 + y2.

Перенося в левую часть все слагаемые, получим

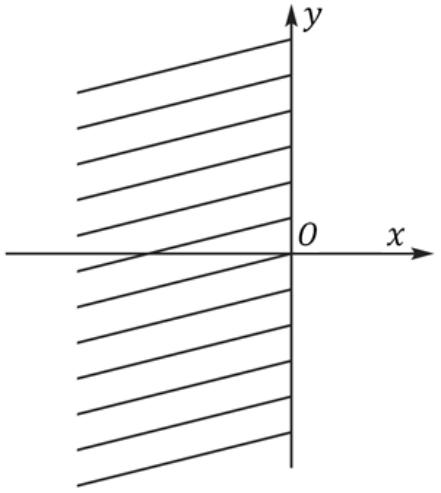
(x − 1)2 − (x + 1)2 ≥ 0 или −4x ≥ 0, или x ≤ 0 – это левая полуплоскость вместе с границей x = 0 (см. рис. 10 ).

ству Кафедра	МИРЭА
Рис.10
Тема 2. Функции комплексного переменного
МГТУ

2.1 Определение функции комплексного переменного.

Определение 2.1. δ-окрестностью точки z0 называется множество точек z, лежащих внутри круга радиуса δ с центром в точке z0, т.е. множество точек, удовлетворяющих неравен-

|z − z0| < δ.

Определение 2.2. Областью комплексной плоскости назы-

вается множество точек D, обладающее следующими свойствами:

1.вместе с каждой точкой из D этому множеству принадлежит и некоторая окрестность этой точки, то есть некоторый круг без границы с центром в этой точке (свойство открытости);

2.две любые точки D можно соединить ломаной, состоящей из точек D (свойство связности).

Определение 2.3. Область называется односвязной, если
		2
любую замкнутую кривую, лежащую в этой области, можно
	-
стянуть в точку, не выходя за пределы этой области.
	ВМ
функция w = f(z), если каждой точке z МИРЭАD поставлено в со-
Определение 2.4. Граничной точкой области D называют
такую точку, которая сама не принадлежит D, но в любой
окрестности которой лежат точки этой области.
Определение 2.5. Совокупность граничных точек области
Кафедра
D называют границей этой области.

Определение 2.6. Область D с присоединенной к ней грани-

цей называется замкнутой областью и обозначается D.

Определение 2.7. Говорят, что в области D определена

ответствие одноМГТУ(однозначная функция) или целое множество

(многозначная функция) значений w.

Пример 2.1.

w = |z| – однозначная функция,

√

w = n z – n-значная функция, т.к. имеет n корней,

w = Arg z – бесконечнозначная функция, т.к. слагаемое 2πk, входящее в Arg z (см. (1.3)), принимает бесконечное число значений при k = 0, ±1, ±2, . . .

Геометричеcки задание функции w = f(z) означает задание отображения точек комплексной плоскости z на соответствующие точки комплексной плоскости w.

Пусть z = x + iy и w = f(z), тогда

w = f(z) = u(x, y) + iv(x, y),

(2.1)

где u(x, y) = Re f(z) – действительная часть функции, v(x, y) = Im f(z) – мнимая часть функции.

Пример 2.2.

Найти действительную и мнимую части функции w = z2 + iz.

Положим z = x + iy, тогда w = (x + iy)2 + i(x					iy) = x2 +
2		2	2	-
2xyi − y	+ ix	+ y = (x	− y	+ y) + i(2xy + x). u(x, y) = x 2− y + y –
				ВМ
действительная часть функции, v(x, y) = 2xy + x – мнимая часть
a0zn + a1zn−1		+ . . . + an.		МИРЭА
функции.

2.2 Элементарные функции комплексного переменного.

Основные элементарные функции комплексного переменного определяютсяКафедраследующими формулами (z = x + iy)

1. Дробно-рациональная функция

w = a0zn + a1zn−1 + . . . + an . b0zm + b1zm−1 + . . . + bm

В частности, рациональной функцией является многочлен w =

но сходящегося во всей комплексной плоскости степенного ряда

2. ПоказательнаяМГТУфункция ez определяется как сумма абсолют-

ez = 1 + z + z2 + . . . + zn + . . .

2! n!

Свойства показательной функции:

а) ez1+z2 = ez1 ez2 , где z1, z2 – комплексные числа,

в) ez+2πki = ez (k = 0, ±1, ±2, . . .) – было показано в примере (6.22), т.е. ez – периодическая функция с периодом 2πi.

3. Тригонометрические функции.

Функции sin z и cos z определяются степенными рядами


	z3				. . . + (−1)n			z2n+1
sin z = z −			+							+ . . . ,
	3!							(2n + 1)!
		z2				z4			z2n
cos z = 1 −				+			+ . . . + (−1)n				+ . . . ,
		2!				4!			(2n)!

абсолютно сходящимися при любом комплексном z.

sin z и cos z – периодические функции с периодом T = 2π.

sin z

= 0 имеет решение z

= kπ, cos z

= 0 имеет решение

z =

+ kπ, k = 0, ±1, ±2, . . .

ВМ

МИРЭА

- sin z

Функции tg z и ctg z определяются равенствами tg z =

cos z ,

ctg z =

cos z

. Для тригонометрических функций остаются в силе

sin z

все формулы тригонометрии.

Для функций ez, sin z и cos z имеют место формулы Эйлера

Кафедраch z sh z

i sin z,

eiz = cos z

+ i sin z,

e−iz = cos z

−

откуда

eiz + e−iz

eiz − e−iz

cos z =

sin z =

(2.2)

4. Гиперболические функции.

МГТУ

Гиперболические функции sh z, ch z

, th z, cth z определяются

равенствами

sh z =

ez − e−z

, ch z =

ez + e−z

(2.3)

th z =

sh z

, cth z =

ch z

5. Связь между тригонометрическими и гиперболическими функ-

циями

sin z = −i sh iz,

cos z = ch iz,

tg z = −i th iz,

(2.4)

ctg z = i cth iz,

sh z = −i sin iz,

ch z = cos iz,

th z = −i tg iz,

cth z = i ctg iz.

6. Логарифмическая функция Ln z, где z =6 0, определяется как функция, обратная показательной, причем

Ln z = ln |z| + i Arg z = ln |z| + i(arg z + 2πk),

(2.5)

k = 0, ±1, ±2, . . .

Функция w = Ln z является многозначной.

Определение 2.8. Главным значением Ln z называется зна-

чение, получаемое при k = 0									-
		ln z = ln \|z\| + i arg z.							-
		ln z = ln \|z\| + i arg z.							2(2.6)
							ВМ
Тогда (2.5) перепишется в виде:							МИРЭА
Тогда (2.5) перепишется в виде:					Ln z = ln z				+ 2πki
Свойства: w = Ln z:
	a) Ln(z1z2) = Ln z1					+ Ln z2,
Кафедра
	b) Ln		z1
	b) Ln		z2	= Ln z1 − Ln z2.
7. Общая показательная функция определяется равенством
			az = ez Ln a,						(2.7)
	МГТУ
a – любое комплексное число, a					6= 0.
8. Общая степенная функция w = zα, где α – любое комплекс-
ное число, z 6= 0			zα = eα Ln z.						(2.8)
Пример 2.3.
Вычислить Ln(−1).
Из формулы (2.5)		k = 0, ±1, ±2, . . .
= (2k + 1)πi,		k = 0, ±1, ±2, . . .
Ln(−1) = ln \| − 1\| + i arg(−1) + 2πk								= i(π + 2πk) =

Пример 2.4.

Вычислить sin(3 − i).

Используя формулы (2.2) перепишем sin(3

−

i), т.к.

sin z =

eiz − e−iz

, то

(3 i)

1+3i

sin(3i− i) =

ei(3−i) − e−i 1−

= −

− e− −

e(cos 3 + i sin 3)

e− (cos 3 − i sin 3)

−

e−1

−

e + e−1

= −ih cos 3

−

+ i sin 3

-2

|i| = 0 + 1

= 1,

ВМ

ln |i| = ln 1 = 0МИРЭА, arg i = 2 ,

= sin 3 ch 1 − i cos 3 sh 1.

Пример 2.5.

Вычислить i2i.

Положим a = i, z = 2i и воспользуемся формулой (2.7)

Кафедра

i2i = e2i Ln i.

Вычислим отдельно Ln i. Используя формулу (2.5), получим:

Ln i = ln |i| + i

arg i + 2πk

= i

+ 2πk ,

√

МГТУ

2, . . .

i2i = e2i·i( π2 +2πk)

= e−π−4πk,

k = 0,

Пример 2.6. Решить уравнение sin z =

3, корни уравнения

изобразить на комплексной плоскости .

Используя формулу (2.2), уравнение можно переписать в виде

eiz − e−iz

= 3

2iz

6ie

1 = 0

– это квадратное уравнение относительно

или e

−

. Его корни

√

= 3i ± 2 2 i = i(3 ± 2 2)

Прологарифмируем полученное равенство

√

arg (3

+ 2

= 0

= Ln i(3 ± 2

= ln i(3 ± 2

√

(2.9)

√

πk ,

, . . .

Вычислим i(3±2

= 3 ± 2

, arg

и подставим

i(3±2

в (2.9),

получим

√

+ 2πk ,

iz = ln(3 ± 2

2) + i

отсюда вычислим

+ВМ2πk − i ln(3 − 2

z1 =

+ 2πk − i ln(3 + 2

2),

2).

√

МИРЭА√

z =

i ln(3 ± 2

2) +

+ 2πk =

2 + 2πk

− i ln(3 ± 2 2).

Получили две серии корней

√

Кафедра

Преобразуем z2.

√

− ln(3 − 2

2). = ln

3 − 2

= ln(3 + 2

2),

поэтому

МГТУ

+ 2πk

+ i ln(3 + 2

2).

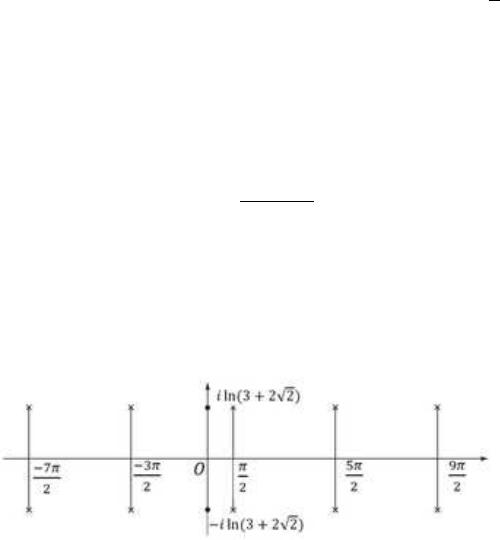
Корни находятся на двух прямых, параллельных оси Ox и отсто-

√

ящих от нее на расстояние ln(3 + 2). На рис.11 корни отмечены ” × ”.

Рис.11

2.3Предел и непрерывность функции комплексного переменного.

Определение 2.9. Число A называется пределом функции f(z) в точке z0, если для любого числа ε > 0 можно указать такое число δ = δ(ε) > 0, что для всех точек z, удовлетворяющих условию 0 < |z − z0| < δ выполняется неравенство |f(z) − A| < ε.

В этом случае пишут z→z0 (	) =				0		=	(	) :		:
lim f z		A		ε >		δ		δ ε		z

0 < \|z − z0\| < δ \|f(z) − A\| < ε.					2
0 < \|z − z0\| < δ \|f(z) − A\| < ε.				z0 и A – конечные точки
комплексной плоскости.
				ВМ
				МИРЭА
Определение 2.10. Функция f(z), заданная в области- D, на-
зывается непрерывной в точке	z	0	D	, если z z0 (	) =	(	0).
	z		D	lim f z		f z

→

Теорема 2.1. Для того, чтобы функция комплексной переменной f(z) = u(x, y) + iv(x, y) была непрерывна в точке z0 = x0 + iy0, необходимо и достаточно, чтобы функции u(x, y) и v(x, y) были непрерывны в точке M0(x0, y0) по совокупности пе-

ременных x и y.

Пример 2.7.
Вычислить предел функции	lim	z2	+ iz + 2	.
			z + 2i
	z→−2i

Решение: Непосредственная подстановка в числитель и знаменатель предельного значения аргумента z = −2i обращает их в

нуль и приводит к неопределенности вида

. Разложим числи-

тель и знаменатель на множители, выделяя множитель (z + 2i):

Кафедра

lim

z2 + iz + 2

lim

(z + 2i)(z − i)

lim (z

−

i) =

−

3i.

z + 2i

→−

z + 2i

→−

МГТУ

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.05.2015148.02 Кб13TrAlg1s.pdf
#
10.05.2015216.89 Кб16TrAlg2s.pdf
#
14.08.2019346.62 Кб7transportirovka-postradavshego.doc
#
10.05.2015171.63 Кб13TR_1sem.pdf
#
10.05.2015266.27 Кб28Tr_ma1s_pdf.pdf
#
10.05.2015716.58 Кб24Tr_ma4s.pdf
#
10.05.2015716.58 Кб22Tr_ma4s_0.pdf
#
19.09.2019146.43 Кб7TSPP.doc
#
10.05.20154.13 Mб10TVizbor_privet_privet.pdf
#
10.05.2015816.7 Кб65TXT.rtf
#
10.05.2015295.27 Кб8UMK_Inform_teh_bak.pdf