Лекции / L12

Матрица системы (11.20) трёхдиагональная.

Решения находят методом прогонки.

Решив её, находим затем коэффициенты из уравнений (11.18) и (11.19), и - из уравнений (11.17).

Метод сплайн-интерполяции приводит к удовлетворительным результатам в процессе интерполяции непрерывных функций с гладкой 1-й и 2-й производными. Сплайн-интерполяция функций с резким изменением производных сплайн не может давать не может давать большие ошибки. Сплайны более высокого порядка, чем 3-й, используют редко, т.к. при вычислении большого числа коэффициентов могут накапливаться ошибки, приводящие к значительным отклонениям.

Существуют и другие формулы интерполяции.

В реальных условиях задача часто состоит в том, чтобы найти приближённую зависимость , значения которой при мало отличаются от опытных данных . Приближённая функциональная зависимость, полученная на основании экспериментальных данных, называется эмпирической формулой.

Построение эмпирической формулы состоит из двух этапов подбора общего вида этой формулы и определения наилучших значений содержащихся в ней параметров. Предпочтение обычно отдаётся наиболее простым формулам, обладающим достаточной точностью. Они первоначально выбираются из геометрических соображений: экспериментальные точки наносятся на график, и примерно угадывается общий вид зависимости путём сравнения полученной кривой с графиками известных функций: показательной или логарифмической функций и т.п.

Будем считать, что тип эмпирической зависимости выбран, и её можно представить в виде

(12.1)

где - известная функция

- неизвестные постоянные параметры.

Задача состоит в том, чтобы определить такие значения этих параметров, при которых эмпирическая формула даёт хорошее приближение данной функции, значения которой в точках равны . Здесь не ставится условие совпадения опытных данных со значениями эмпирической функции (12.1) в точках ( как в случае интерполяции).

Разность между этими значениями – отклонения – обозначим через .

, i=0,1…,n (12.2)

Метод наименьших квадратов.

Существуют достаточно простые методы определения параметров эмпирической формулы: метод выбранных точек, метод средних и др. Однако часто получаемые с их помощью аппроксимации не обладают достаточной точностью.

Запишем сумму квадратов отклонений для всех точек :

(12.3)

Параметры эмпирической формулы находят из условия минимума функции . В этом состоит метод наименьших квадратов.

В теории вероятностей доказывается, что полученные таким методом значения параметров наиболее вероятны, если отклонения подчиняются нормальному закону распределения.

Поскольку здесь параметры выступают в роли независимых переменных функции S, то её min можно найти, приравнивая к Ø частные производные по этим переменным:

Эти соотношения -

4. система уравнений

для определения

.

Рассмотрим применение метода наименьших квадратов для широко используемого на практике частного случая, когда функция является линейной по неизвестным параметрам :

где известные функции x.

j=0,…,m.

Формула (12.3) примет вид:

Для составления системы (12.4) дифференцируем S по переменным

Приравнивая найденные производные к Ø, получим систему уравнений:

k=0,…m (12.5)

Система (12.5) является СЛАУ, её можно записать в матрично-векторном виде, введя следующие обозначения:

-вектор опытных данных

Размерности n+1

…

-вектор размерности

… неизвестных параметров

Матрица

размерности Ф=

(n+1)*(m+1)=Ф

Для элементов матрицы справедливо выражение:

Систему (12.5) можно записать в виде:

или

(12.6)

Действительно:

- выражение в квадратных скобках в системе (12.5) является i-ой компонентой вектора ;

- каждое уравнение (12.5) представляет собой равенство Ø к-ой компоненты вектора , где транспонированная матрица.

Матрица системы (12.6) имеет размерность (m+1)x(m+1); вектор a - искомый вектор.

Ещё несколько замечаний:

1.Можно доказать, что если столбцы матрицы Ф линейно независимы, то система (12.6) имеет единственное решение.

Из алгебры матриц: векторы называются линейно независимыми тогда и только тогда, когда никакая линейная комбинация их, не все коэффициенты которой равны Ø, не является нуль-вектором.

2. Матрица является симметричной, т.е.

3. В случае использования в качестве эмпирической функции многочлена вида

элементы матрицы и компоненты вектора y можно вычислить по формулам:

(12.7)

В частности, равны все элементы при

Пример: Используя метод наименьших квадратов, вывести эмпирическую формулу для функции , заданную таблично:

x	0,75	1,50	2,25	3,00	3,75
y	2,50	1,20	1,12	2,25	4,28

Решение: Если изобразить данные табличные значения на графике, то легко убедиться, что в качестве эмпирической формулы для аппроксимации функции можно принять квадратный трехчлен, графиком которого является парабола:

В данном случае имеем

2,50 1,20 y= 1,12 2,25 4,28

а=

Ф=

1 1 1 1 1

0,75 1,50 2,25 3,00 3,75

Необходимо вычислить матрицу и вектор y (округляем значения до 2-х знаков после запятой)

	5	11,25	30,94		11,35
=	11,25	30,94	94,92	y=	29,00
	30,94	94,92	309,76		90,21

Система уравнений (12.6) примет вид:

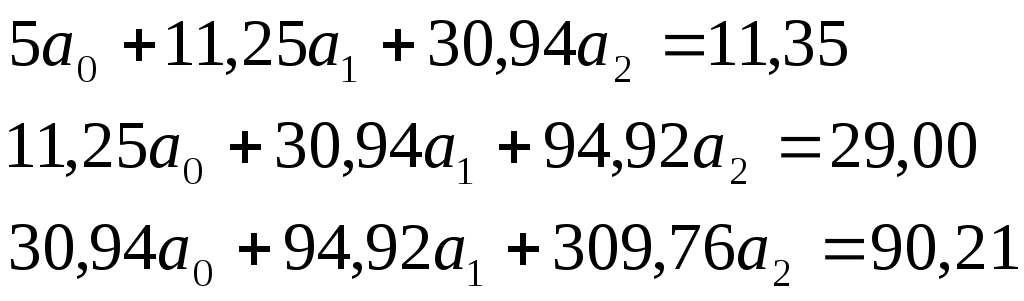
Отсюда, значения параметров эмпирической формулы:

Таким образом, получаем аппроксимацию функции, заданной в табличном виде:

Оценим относительные погрешности полученной аппроксимации в заданных точках, т.е. найдём значения

Результаты вычислений:

x		y
0,75	2,47	2,50	-0,03	-0,012
1,50	1,25	1,20	0,05	0,042
2,25	1,15	1,12	0,03	0,027
3,00	2,17	2,25	-0,08	-0,036
3,75	4,32	4,28	0,04	0,

Дифференцирование и интегрирование.

Численное дифференцирование.

При решении практических задач часто нужно найти производные указанных порядков от функции , заданной таблично, либо аналитически, но непосредственное дифференцирование которой по каким-либо причинам затруднено. Напомним, что производной функции называется предел отношения приращения функции к приращению аргумента при стремлении к Ø:

(12.8)

В численных расчётах на компьютере использование готовых формул из таблиц производных не всегда удобно и возможно, в частности в случае, если функция задана в виде таблицы значений. Тогда для вычисления производной используют приближенное равенство

(12.9)

Это соотношение называется аппроксимацией (приближением) производной с помощью отношения конечных разностей.

Значения и в (12.9) конечные в отличие от их бесконечно малых значений в (12.8)

Рассмотрим аппроксимацию производной для функции , заданной в табличном виде

Y					…
в узлах x					…

Пусть шаг

Запишем выражения для производной в узле .

В зависимости от способа вычисления конечных разностей получаем разные формулы для вычисления производной в одной и той же точке:

с помощью левых разностей:

(12.10)

с помощью павых разностей:

(12.11)

с помощью центральных разностей:

(12.12)

Выражение для 2-й производной:

(12.13) и т.д.

Таким образом, используя формулу (12.9), можно найти приближённые значения производных любого порядка. Однако для хорошей аппроксимации производной лучше использовать значения функции во многих узлах, а в формуле (12.9) это не предусмотрено.

Для вывода формул приближённого дифференцирования данную функцию f(x) на отрезке [a,b] заменяют аппроксимирующей функцией , т.е. представляют в виде

(12.14)

где R(x) -погрешность аппроксимации.

В качестве аппроксимирующей функции может быть использована частичная сумма ряда или интерполяционная функция, чаще всего полином.

Дифференцируя равенство(12.14) необходимое число раз, можно найти значения производных

Отсюда

Т.е. погрешность производной аппроксимирующей функции равна производной от погрешности этой функции. То же справедливо и для производных высших порядков.

Погрешность аппроксимации – один из источников погрешности численного дифференцирования. С увеличением h эта погрешность увеличивается.

Существуют также погрешности, обусловленные неточными значениями функции в узлах, погрешности округлений при проведении компьютерных расчётов. Эти погрешности увеличиваются с уменьшением шага h.

Действительно, если при вычислении значений функции абсолютная погрешность составляет d, то при вычислении дробей в (12.10) и (12.11) она составит . Поэтому суммарная погрешность численного дифференцирования может уменьшаться при уменьшении шага лишь до некоторого предельного значения, после чего дальнейшее уменьшение шага не увеличит точности результатов.

Потеря точности аппроксимации производных может быть предотвращена за счёт регуляризации процедуры численного дифференцирования. Простейшим способом регуляризации является такой выбор шага h, при котором справедливо неравенство , где - некоторое малое число. При вычислении производной это исключает вычитание очень близких по величине чисел, которое, как мы знаем, обычно приводит к увеличению погрешности.

Возможен и ещё один подход – сглаживание табличных значений функции подбором некоторой гладкой аппроксимирующей функции, например, многочлена.

Использование интерполяционных формул

для численного дифференцирования.

Пусть , имеет в равностоящих точках отрезка значения .

Пусть известно, что существуют производные функции до необходимого нам порядка. Для нахождения на соответствующих производных и т. д. Функцию y приближённо заменим интерполяционным многочленом Ньютона (первым интерполяционным многочленом Ньютона для интерполирования вперёд).

Дифференцируя этот многочлен по x с учётом правила дифференцирования сложной функции

можно получить формулы для вычисления производных порядка:

Число слагаемых в этих формулах зависит от количества узлов, используемых для вычисления производных.

Как и при построении многочлена Ньютона, добавление нового узла означает добавление одного слагаемого к сумме.