
Лекции / L5
.docИтерационные методы решения СЛАУ.
Уточнение решения.
Решения, получаемые с помощью прямых методов (например, по методу Гаусса), обычно содержат погрешности вызываемые округлениями при выполнении операций над числами с плавающей точкой на компьютере с ограниченным числом разрядов. В ряде случаев эти погрешности могут быть значительными, и необходимо найти способ их снизить. Рассмотрим один из методов, позволяющий уточнить решение, получаемое с помощью прямого метода.
Найдем решение СЛАУ
Ax = b; (5.1)
Пусть с помощью некоторого прямого метода вычислено приближенное решение

Называемое начальным или нулевым приближением к решению.
Подставляя это решение в левую часть (5.1), получаем некоторый столбец правых частей.
 отличный от b.
отличный от b.
![]() (5.2)
(5.2)
Введем обозначения:
![]() (5.3)
(5.3)
Вычитая (5.2) из (5.1), получим:
![]() (5.4)
(5.4)
Решая эту систему, находим значение
погрешности
![]() ,
которое используем в качестве поправки
к приближенному решению
,
которое используем в качестве поправки
к приближенному решению
![]() ,
вычисляя таким образом новое приближение
(или следующее приближение к решению)
,
вычисляя таким образом новое приближение
(или следующее приближение к решению)
![]() :
:
![]() (5.5)
(5.5)
Таким же образом можно вычислить новую
поправку к решению
![]() и следующее приближение:
и следующее приближение:
![]() и т.д.
и т.д.
Процесс продолжается до тех пор, пока
очередное значение погрешности (поправки)
![]() не станет достаточно малым. Рассмотренный
процесс уточнения решения представляет
собой фактически итерационный метод
решения СЛАУ. Заметим, для нахождения
очередного приближения (на каждой
итерации) решаются системы уравнений
вида (5.4) с одной и той же матрице,
являющейся матрицей исходной системы
(5.1), при разных правых частях. Это
позволяет строить экономичные алгоритмы.
Например, при использовании метода
Гаусса сокращается объём вычислений
на этапе прямого хода. Решение систем
линейных уравнений с помощью рассмотренного
итерационного метода сводится к следующей
схеме:
не станет достаточно малым. Рассмотренный
процесс уточнения решения представляет
собой фактически итерационный метод
решения СЛАУ. Заметим, для нахождения
очередного приближения (на каждой
итерации) решаются системы уравнений
вида (5.4) с одной и той же матрице,
являющейся матрицей исходной системы
(5.1), при разных правых частях. Это
позволяет строить экономичные алгоритмы.
Например, при использовании метода
Гаусса сокращается объём вычислений
на этапе прямого хода. Решение систем
линейных уравнений с помощью рассмотренного
итерационного метода сводится к следующей
схеме:
-
Ввод исходных данных: например коэффициенты уравнений допустимые погрешности.
-
Задаются начальные значения неизвестных (вектор столбец
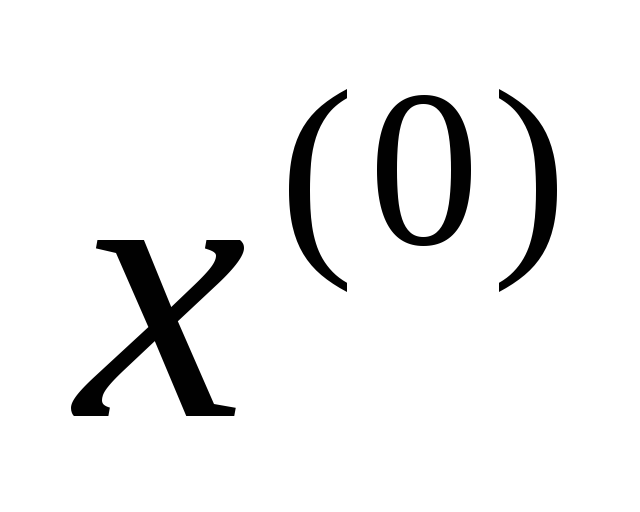 ):
):
-
либо вводится в компьютер
-
либо вычисляется каким-либо способом (например, решая СЛАУ прямым методом))
Циклический вычислительный процесс,
на каждом шаге (итерации) которого
вычисляется следующее приближение
![]() по предыдущему
по предыдущему
![]() До
тех пор, пока
До
тех пор, пока
![]() -
малая величина, заданная допустимая
погрешность.
-
малая величина, заданная допустимая
погрешность.
-
Вывод результатов: вывод x.
Метод называют сходящимся, если с увеличением числа итераций приближенное решение стремится к точному:
![]() (5.6)
(5.6)
На практике наличие сходимости и
достижение требуемой точности обычно
определяют приближенно, поступая
следующим образом: при малом изменении
x на двух последовательных
итерациях, т.е. при заданной допустимой
погрешности
![]() мало отличной от
мало отличной от
![]() процесс прекращается и происходит вывод
значений
процесс прекращается и происходит вывод
значений
![]() -
неизвестных полученных на последней
итерации.
-
неизвестных полученных на последней
итерации.
Возможны разные подходы к определению
малости отличия
![]() от
от
![]() .
.
Например: если задана допустимая погрешность , то критерием окончания итерационного процесса можно считать выполнение одного из условий:
![]() (5.7)
(5.7)
![]() (5.8)
(5.8)
 ,
при
,
при
![]() (5.9)
(5.9)
(5.7) – в смысле малости модуля разности
(5.8) – в смысле малости разностей соответствующих компонентов векторов
(5.9) – в смысле малости относительных разностей компонентов.
Можно испытать и условие малости невязки:
![]() (5.10)
(5.10)
Для предотвращения непроизвольных затрат машинного времени в случае отсутствия сходимости в алгоритм вводят счетчик числа итераций, и при достижении им некоторого заданного счет прекращается.
Метод простой итерации
При большом числе неизвестных линейной системы схема метода Гаусса, задающая точное решение, становится весьма сложной. В этих условиях для нахождения корней системы иногда удобнее пользоваться приближенными численными методами.
Рассмотрим систему вида (5.1)
Ax = b
Предположим, что дополнительные коэффициенты
![]()
Решим первое уравнение системы
относительно
![]() ,
второе относительно
,
второе относительно
![]() и т.д. Получим эквивалентную систему:
и т.д. Получим эквивалентную систему:
 (5.11)
(5.11)
где
![]()
и
![]()
Введем матрицы:
 ,
,
![]()
систему (5.11) запишем в матричном виде
![]() (5.12)
(5.12)
Будем искать решение (5.12) методом последовательных приближений. За нулевое приближение примем, например, столбец свободных членов
![]()
Подставим его в правую часть системы (5.12) и получим первое приближение
![]() и т.д.
и т.д.
(k+1) – е приближение вычисляется по формуле:
![]() (5.13)
(5.13)
Если последовательность приближений
![]() имеет предел
имеет предел
![]()
то этот предел является решением системы (5.12)
Запишем формулы приближений в развернутом виде
 (5.14)
(5.14)
Заметим. Что иногда выгоднее систему
(5.1) приводить к виду (5.12) так, чтобы
![]() например уравнение
например уравнение
![]() можно записать так
можно записать так
![]()
Вообще, имея систему
![]()
можно положить
![]()
где
![]() .
Тогда данная система эквивалентна
системе
.
Тогда данная система эквивалентна
системе
![]()
где

Поэтому при дальнейших рассуждениях
мы не будем предполагать, что
![]() .
.
Рассмотрим пример: решим систему методом итерации
 (5.15)
(5.15)
Здесь диагональные коэффициенты 4; 3; 4 системы значительно преобладают над остальными коэффициентами при неизвестных. Приведем эту систему к нормальному виду (5.12):
 (5.16)
(5.16)
В матричной форме это можно записать так

За нулевое приближение систему (5.15)
примем
![]()
Подставляя эти значения в правые части уравнений (5.16), поучим 1-ое приблидение корней:
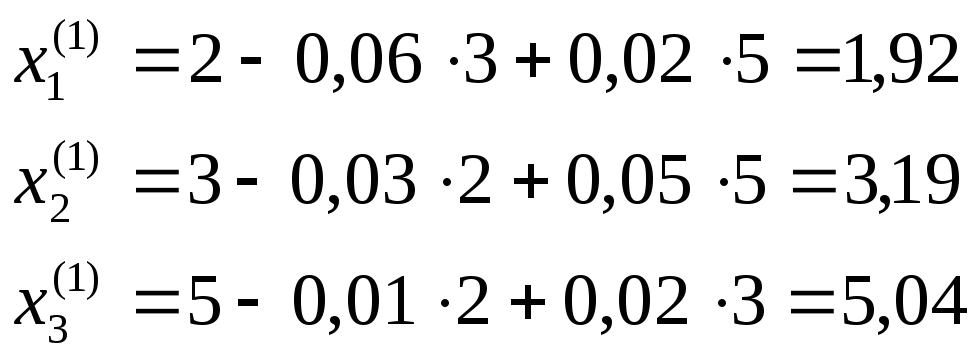
Потом, подставляя эти найденные приближения в формулу (5.16), получим 2ое приближение корней:

3е приближение корней:
 и т.д.
и т.д.
Важное свойство сходящегося процесса итерации:
Самоисправляемость, т.е. отдельная ошибка в вычислениях не отразится на окончательном результате, т.к. ошибочное приближение можно рассматривать как новый начальный вектор.
Иногда бывает удобно подсчитывать не сами приближения, а их разности:
![]()
Достаточное условие сходимости процесса итерации сформулированы в теореме:
Если для приближенной системы (5.11) выполнено, по меньшей мере, одно из условий
1)
![]()
или
2)
![]()
то процесс итерации (5.13) сходится к единственному решению этой системы, независимо от выбора начального приближения.
Следствие: Для системы
![]()
метод итерации сходится, если выполнены неравенства
![]()
т.е. если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
То сходимость процесса итерации зависит только от свойств матрицы .
Под нормой матрицы
![]() понимается действительное число
понимается действительное число![]() ,
удовлетворяющее условиям:
,
удовлетворяющее условиям:
а)
![]() ;
причем
;
причем
![]() ,
тогда только тогда, когда A=
0;
,
тогда только тогда, когда A=
0;
б)
![]() ( - число), в частности
( - число), в частности
![]()
в)
![]()
г)
![]()
Норма называется канонической, если дополнительно выполнены условия:
д) если
![]()
причем для скалярной матрицы
![]()
е) из неравенства
![]() следует неравенство
следует неравенство
![]()
A и B – матрицы
В частности,
![]() .
.
Достаточное условие сходимости процесса итерации можно сформулировать, используя понятие нормы матрицы: Процесс итерации для приведенной линейной системы
![]()
Сходится к единственному её решению,
если какая-нибудь каноническая норма
матрицы
![]() .
(
.
(![]() - произвольно)
- произвольно)
Следствие: процесс итерации для приведенной линейной системы сходится, если
а)
![]()
или
б)
![]()
или
в)
![]()
В частности, процесс итерации заведомо сходится, если элементы матрицы удовлетворяют неравенству
![]() , где n – число неизвестных
в системе.
, где n – число неизвестных
в системе.
Пример вычисления норма матрицы:
Пусть

Имеем:
![]()
![]()
![]()
Одним из самых распространенных
итерационных методов, отличающихся
простотой и легкостью программирования,
является метод Гаусса - Зейделя. Он
являет собой некоторую модификацию
метода итерации. Основная его идея
заключается в том, что при вычислении
(к+1)го приближения неизвестной
![]() учитывается уже вычисленные ранее
(k+1)е приближения неизвестных
учитывается уже вычисленные ранее
(k+1)е приближения неизвестных
![]() .
.
Пусть дана приведенная линейная система
![]()
Выберем произвольно начальное приближение
корней
![]() стараясь, конечно, чтобы они в какой-то
мере соответствовали искомым неизвестным
стараясь, конечно, чтобы они в какой-то
мере соответствовали искомым неизвестным
![]() .
Предполагая, что k-ое
приближение корней
.
Предполагая, что k-ое
приближение корней
![]() известны, согласно методу Гаусса -
Зейделя будем строить (k+1)-е
приближение корней по следующим формулам:
известны, согласно методу Гаусса -
Зейделя будем строить (k+1)-е
приближение корней по следующим формулам:
 (5.17)
(5.17)
*
Заметим, что теорема сходимости для простой итерации остается верной для итерации по методу Гаусса - Зейделя.
Пример: решим методом Зейделя систему уравнений:

Приведем систему к виду, удобному для итераций:

Выберем нулевое приближение корней:
![]()
Применяем процесс Зейделя:

ещё раз:
 и т.д.
и т.д.
Результаты вычислений с точностью до 4-х знаков:
|
k |
|
|
|
|
0 |
1,2000 |
0,0000 |
0,0000 |
|
1 |
1,2000 |
1,0600 |
0,9480 |
|
2 |
0,9992 |
1,0054 |
0,9991 |
|
3 |
0,9996 |
1,0001 |
1,0001 |
|
4 |
1,0000 |
1,0000 |
1,0000 |
|
5 |
1,0000 |
1,0000 |
1,0000 |
Т.о. точные значения корней:
![]() .
.
