
Задачи для подготовки к экзамену-2сем
.docxЗадачи.
Алгебра .2 семестр.РТС.
I Комплексные числа.
-
Вычислить
 ,
ответ представить в алгебраической
форме и изобразить на комплексной
плоскости.
,
ответ представить в алгебраической
форме и изобразить на комплексной
плоскости. -
Вычислить
 .
Ответ
представить в алгебраической форме и
изобразить на комплексной плоскости.
.
Ответ
представить в алгебраической форме и
изобразить на комплексной плоскости.
-
Вычислить
 ,
результат изобразить на комплексной
плоскости.
,
результат изобразить на комплексной
плоскости.
-
Решить уравнение. Ответ представить в алгебраической форме и изобразить на комплексной плоскости. z

II Линейные пространства.
1.Является
ли множество
 векторов
заданного
вида линейным подпространством в
векторов
заданного
вида линейным подпространством в

 ?
Если да, то найти базис и размерность
этого подпространства
?
Если да, то найти базис и размерность
этого подпространства
 .
Дополнить базис подпространства
.
Дополнить базис подпространства
 до
базиса всего пространства.
до
базиса всего пространства.
2.Показать,
что многочлены

 ;
;



 образуют
базис пространства
образуют
базис пространства
 .
Найти координаты вектора g(t)=
.
Найти координаты вектора g(t)=
 в
этом базисе. Сделать проверку.
в
этом базисе. Сделать проверку.
3.Проверить,
что множество многочленов
 заданного
вида
с
вещественными коэффициентами образует
подпространство в линейном пространстве
заданного
вида
с
вещественными коэффициентами образует
подпространство в линейном пространстве
 многочленов
степени не выше 2.
Найти размерность и базис L,
дополнить его до базиса всего пространства
многочленов
степени не выше 2.
Найти размерность и базис L,
дополнить его до базиса всего пространства
 .
.
4.
Доказать, что векторы
 =
=
 +
+
 =
= +
+ и
и
 =
=
 +
+
 образуют
базис в пространстве геометрических
векторов. Найти координаты вектора
образуют
базис в пространстве геометрических
векторов. Найти координаты вектора =
–
=
– +
2
+
2 -
- в
этом базисе.
в
этом базисе.
III Линейные операторы.
-
В пространстве V
 линейный оператор
линейный оператор
 -поворот
против часовой стрелки на угол
-поворот
против часовой стрелки на угол
 вокруг оси ОY.
вокруг оси ОY.
-
Найти матрицу оператора A в базисе
 .
. -
Найти образ вектора

-
Найти ядро и образ оператора А.
-
Существует ли обратный оператор? Если да, то описать его действие.
-
Найти собственные значения и собственные векторы оператора
 .
Является ли он оператором простого
типа?
.
Является ли он оператором простого
типа?
-
-
В пространстве V
 линейный оператор
линейный оператор
 -
зеркальное отражение относительно оси
ОХ.
-
зеркальное отражение относительно оси
ОХ.
-
Найти матрицу оператора A в базисе
 .
. -
Найти образ вектора

-
Найти ядро и образ оператора А.
-
Существует ли обратный оператор? Если да, то описать его действие.
-
Найти собственные значения и собственные векторы оператора
 .
Является ли
.
Является ли
 оператором простого типа?
оператором простого типа?
-
-
В пространстве V
 линейный оператор
линейный оператор
 -
зеркальное отражение относительно
плоскости XОY.
-
зеркальное отражение относительно
плоскости XОY.
-
Найти матрицу оператора A в базисе
 .
. -
Найти образ вектора

-
Найти ядро и образ оператора А.
-
Существует ли обратный оператор? Если да, то описать его действие.
-
Найти собственные значения и собственные векторы оператора
 .
Является ли
.
Является ли
 оператором простого типа?
оператором простого типа?
-
-
В пространстве V
 линейный оператор
линейный оператор
 -
проекция на ось ОY.
-
проекция на ось ОY.
-
Найти матрицу оператора
 в базисе
в базисе .
. -
Найти образ вектора

-
Найти ядро и образ оператора

-
Существует ли обратный оператор? Если да, то описать его действие.
-
Найти собственные значения и собственные векторы оператора
 .
Является ли
.
Является ли
 оператором простого типа?
оператором простого типа?
-
-
В пространстве V
 линейный оператор
линейный оператор
 -
проекция на плоскость YOZ.
-
проекция на плоскость YOZ.
-
Найти матрицу оператора
 в базисе
в базисе .
. -
Найти образ вектора

-
Найти ядро и образ оператора

-
Существует ли обратный оператор? Если да, то описать его действие.
-
Найти собственные значения и собственные векторы оператора
 .
Является ли
.
Является ли
 оператором простого типа?
оператором простого типа?
-
-
В пространстве V
 линейный оператор
линейный оператор
 –
гомотетия с коэффициентом к= -7.
–
гомотетия с коэффициентом к= -7.-
Найти матрицу оператора
 в базисе
в базисе .
. -
Найти образ вектора

-
Найти ядро и образ оператора

-
Существует ли обратный оператор? Если да, то описать его действие.
-
Найти собственные значения и собственные векторы оператора
 .
Является ли
.
Является ли
 оператором простого типа?
оператором простого типа?
-
7.
В пространстве P оператор
оператор
 действует по правилу
действует по правилу
 p(t)=2
p(t)=2 .
.
1)
Показать , что
 линейный оператор в P
линейный оператор в P .
.
2) Найти матрицу оператора в каноническом базисе пространства.
3)
Найти ядро и образ оператора
 .
.
4)
Обратим ли оператор? Если
да, то указать явный вид обратного
оператора.
Если
да, то указать явный вид обратного
оператора.
5)
Найти собственные значения и собственные
векторы оператора
 .
.
Является
ли оператор
 оператором простого типа? Если да, то
указать базис из собственных векторов
и матрицу оператора в собственном
базисе.
оператором простого типа? Если да, то
указать базис из собственных векторов
и матрицу оператора в собственном
базисе.
-
В каноническом базисе пространства R
 оператор
оператор
 действует по правилу
действует по правилу
a)

 =(3
=(3 ,
,
 ,
,
 );
);
1)
Показать линейность оператора
 .
.
2) Найти матрицу оператора в каноническом базисе пространства.
3)
Найти ядро и образ оператора
 .
.
4)
Обратим ли оператор?
 Если
да, то указать явный вид обратного
оператора.
Если
да, то указать явный вид обратного
оператора.
5)
Найти собственные значения и собственные
векторы оператора
 .
.
Является
ли оператор
 оператором простого типа? Если да, то
указать базис из собственных векторов
и матрицу оператора в этом базисе.
оператором простого типа? Если да, то
указать базис из собственных векторов
и матрицу оператора в этом базисе.
9.
Линейный оператор
 в базисе (
в базисе ( ,
, ,
, )
задан матрицей A.
Найти матрицу оператора
)
задан матрицей A.
Найти матрицу оператора
 в
базисе (
в
базисе ( ,
, ,
, ).
).

 =
-
=
-
 +
+
 ,
,
 =
2
=
2
 +
+
 ,
,
 =
=
 -
-
 .
.
10.Является ли следующий оператор линейным оператором?
a)
 =(
=(
 +
+ ,
, +
+ ,
, )
)
б)
 =(
=( ,
, +
+ ,
, )
)
с)
 =(
=(
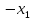 +
+ ,
, +
+ ,
, +
+ )
)
IV Квадратичные формы и евклидовы пространства.
-
Дана квадратичная форма
 =
=

а) Привести к каноническому виду методом Лагранжа, выписать преобразование координат.
б) Найти положительный и отрицательный индексы и ранг формы.
в) Исследовать на знакоопределенность по каноническому виду и по критерию Сильвестра.
-
Дана матрица Грама скалярного произведения G=
 в базисе
в базисе
 .
.
а)
Найти угол между векторами
 и
и
 (-1,3)
(-1,3)
б) Ортогонализировать
базис
 .
Сделать проверку с помощью матрицы
перехода.
.
Сделать проверку с помощью матрицы
перехода.
3. Дана матрица Грама
 =
= в
базисе
в
базисе
 .
.
а) Проверить, что
матрица
 является матрицей Грама.
является матрицей Грама.
б) Найти длины базисных векторов и углы между ними.
в) Найти длины
векторов
 =(1,2,
4) и
=(1,2,
4) и
 =(2,-1,3)
и угол между ними.
=(2,-1,3)
и угол между ними.
Дополнительные задачи.
1.
Разложить многочлен P(z)= на линейные множители.
на линейные множители.
2.Решить уравнение. Ответ представить в алгебраической форме и изобразить на комплексной плоскости.

3.
Установить, являются ли заданные
множества подпространствами в R .
В случае положительного ответа найти
базис и размерность подпространства.
.
В случае положительного ответа найти
базис и размерность подпространства.
1)
Множество векторов, координаты которых
удовлетворяют условию:

2)
Множество векторов, координаты которых
удовлетворяют условию:

3)
Множество векторов, координаты которых
( -
отрицательные числа.
-
отрицательные числа.
4. Пусть L-множество многочленов p(t) степени не выше 2, удовлетворяющих условию:
p(0)=p(1).
Доказать, что L-линейное
подпространство в
 .
Найти его базис и размерность. Дополнить
базис подпространства до базиса всего
пространства.
.
Найти его базис и размерность. Дополнить
базис подпространства до базиса всего
пространства.
5.
В пространстве
 многочленов степени не выше 2 оператор
многочленов степени не выше 2 оператор
 действует по правилу
действует по правилу
 (p(t))
=
(p(t))
=
 .
Доказать, что
.
Доказать, что
 - линейный оператор. Найти его матрицу
в каноническом базисе и в базисе
S=(
- линейный оператор. Найти его матрицу
в каноническом базисе и в базисе
S=( .
.
6.В
пространстве
 многочленов степени не выше 2 оператор
многочленов степени не выше 2 оператор
 действует по правилу
действует по правилу
 (p(t))
= ((t2p(t-2))
(p(t))
= ((t2p(t-2)) .
Доказать, что
.
Доказать, что
 - линейный оператор. Найти его матрицу
в каноническом базисе, найти ядро и
образ оператор. Существует ли обратный
оператор?
- линейный оператор. Найти его матрицу
в каноническом базисе, найти ядро и
образ оператор. Существует ли обратный
оператор?
7.Линейный
оператор
 в пространстве
в пространстве
 в базисе
в базисе
 имеет
матрицу
имеет
матрицу
 .
Найти собственные значения и собственные
векторы оператора
.
Найти собственные значения и собственные
векторы оператора
 .
Является
ли он оператором простого типа? Если
да, то указать базис из собственных
векторов и матрицу оператора в этом
базисе.
.
Является
ли он оператором простого типа? Если
да, то указать базис из собственных
векторов и матрицу оператора в этом
базисе.
8.В
пространстве
 оператор действует по правилу
оператор действует по правилу
 ,
,
 .
Показать линейность оператора, найти
его матрицу в каноническом базисе и в
базисе
.
Показать линейность оператора, найти
его матрицу в каноническом базисе и в
базисе
S
= {
9.В
пространстве
 линейный оператор
линейный оператор
 -
поворот на угол
-
поворот на угол
 по часовой стрелке. Найти матрицу
оператора
по часовой стрелке. Найти матрицу
оператора
 в каноническом базисе. Найти образ
вектора
в каноническом базисе. Найти образ
вектора
 Найти ядро и образ оператора. Существует
ли обратный оператор? Является ли
Найти ядро и образ оператора. Существует
ли обратный оператор? Является ли
 оператором простого типа?
оператором простого типа?
10.Дана матрица Грама
 =
= в
базисе
в
базисе
 .
Ортогонализировать базис S.
.
Ортогонализировать базис S.
