1.3.3 Нахождение кривых высшего порядка

Методика нахождения кривых высшего порядка (эллипсы, параболы и т.д.) отличается от предыдущих подходов размерностью фазового пространства.

Рассмотрим эту особенность на примере детектирования эллипсов. Уравнение, задающее геометрическое место точек эллипса в полярных координатах, принимает вид:

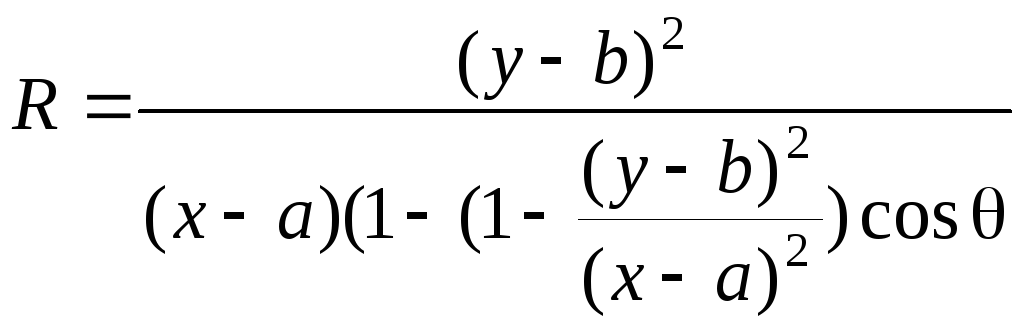
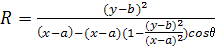(12)

где (a,b) - координаты центра эллипса;

(x,y) - координаты точки на эллипсе;

R, θ - полярные координаты эллипса.

Формула, задающая семейство эллипсов, имеет вид:

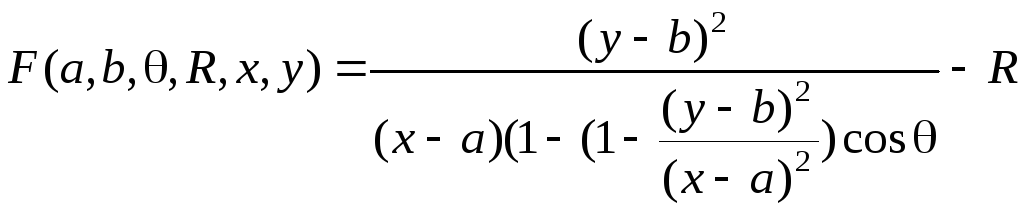
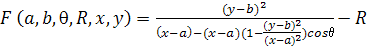, (13)

Для нахождения эллипсов необходимо производить операции в четырехмерном фазовом пространстве. Вычисление фазового пространства для кривых высшего порядка представляет весьма трудоемкую вычислительную задачу, поэтому базовое преобразование Хафа для таких примитивов применяется крайне редко.

1.4 Модификации преобразования Хафа

Преобразование Хафа позволяет проводить полный анализ пространства изображения, но существует ряд проблем, которые влияют на результат и производительность такого подхода:

а) Дискретизация

На шаге 1 выбирается сетка дискретизации. В связи с этим выбором возможны следующие проблемы:

1) Сетка выбрана слишком мелкой. Тогда, если в исходном облаке точек присутствовал шум, то даже точки одной кривой будут попадать в разные ячейки сетки, а значит, потенциальный максимум аккумулятора (соответствующий этой кривой) будет размыт и его будет сложнее или вообще невозможно найти.

2) Сетка выбрана слишком крупной. Тогда существует вероятность того, что в одну ячейку попадут точки, лежащие на разных кривых.

) При любой сетке дискретизации, если точки облака образуют кривую с параметром j₀, лежащим на границе ячейки, то из-за шума точки этой кривой будут попадать в соседние ячейки и будет наблюдаться размытие пика в аккумуляторе. Это вообще фундаментальная проблема дискретизации.

б) Сложность алгоритма.

Заполнение аккумулятора на шаге 2 является самой трудоемкой частью алгоритма, сложность которой зависит от: размерности фазового пространства и сетки дискретизации. Чем больше размерность фазового пространства и меньше сетка, тем больше ячеек в аккумуляторе. Значит, тем больше требуется памяти и времени для его хранения и заполнения. Именно поэтому на практике чаще всего фазовое пространство представляет собой плоскость, а преобразование Хафа применяется, в основном, для поиска прямых на плоскости (изображениях).

В связи с вышеперечисленными проблемами были разработаны некоторые модификации стандартного алгоритма (Standard Hough Transform, SHT).

Комбинаторное преобразование Хафа (Combinatorial Hough Transform) разрабатывалось для быстрого поиска прямых линий на изображении. В таком случае у нас имеется плоское бинарное изображение (на нем точки интереса одного цвета, а точки фона другого). Поскольку производится поиск прямых линий, то размерность фазового пространства равна 2.

Идея метода состоит в изменении шага 2 (заполнение аккумулятора):

а) Исходное бинарное изображение разбивается на небольшие участки.

б) В каждом участке для каждой пары точек определяются параметры (r,q) прямой, проходящей через них.

в) Если (r,q) попадают в некоторую ячейку, и ее счетчик соответственно увеличивается.

Первый шаг модификации необходим для сокращения числа переборов.

Если точек в участке мало и сетка дискретизации фазового пространства тоже мала, количество записей в аккумуляторе получается меньше.

Иерархическое преобразование Хафа (Hierarchical Hough Transform) -это еще одна модификации для поиска линий на бинарном изображении. Приведем последовательность действий для иерархического преобразования:

а) Исходное изображение разбивается регулярной сеткой.

б) В каждом фрагменте изображения выделяются прямые преобразованием Хафа.

в) Производится иерархическое слияние. На каждом уровне рассматриваются 4 соседних фрагмента. Линии, выделенные на каждом из фрагментов, объединяются на основании преобразования Хафа для объединения фрагментов. Если линии не удалось слиться ни с одной линией из соседних фрагментов, она удаляется из рассмотрения.

г) Слияние производится до получения одного исходного изображения.

В результате сложность алгоритма снижается за счет подразбиения изображения (можно использовать более грубую сетку в фазовом пространстве и количество точек существенно меньше).

Недостаток состоит в том, что одна длинная линия может быть в результате представлена несколькими близкими линиями, поскольку разные концы отрезка могут быть неколлинеарными при близком рассмотрении, т.е. на низких уровнях иерархического слияния.

Адаптивное преобразование Хафа (Adaptive Hough Transform) - эта модификация позволяет использовать меньше места для хранения аккумулятора и быстрее выделять кривые [14]. На протяжении всего процесса поиска используется аккумулятор заранее выбранного маленького размера (например, 9?9 или 3?3?3?3 в многомерном случае). Алгоритм выглядит следующим образом:

1) Выбор размера аккумулятора (маленький!).

2) Достижение заданной точности. На каждой итерации размер ячейки уменьшается. Цикл идет до достижения заранее заданного размера ячейки.

) Заполнение аккумулятора. Как и в стандартном варианте, однако меньшая сложность достигается за счет небольшого размера аккумулятора.

) Поиск ячейки с максимальным значением счетчика.

) Ячейка принимается за новое фазовое пространство, переход на шаг 2. Таким образом, мы уменьшаем шаг дискретизации, но только в области интереса (ячейке с максимальным счетчиком).

) Выделяем кривую.

Главными достоинствами адаптивного преобразования Хафа являются:

а) Меньшая сложность по времени и по памяти.

б) Практическое решение проблемы дискретизации, поскольку сетка дискретизации не регулярная и на каждой итерации уточняется.

Основным недостатком алгоритма является следующее. Если исходное облако точек образует несколько кривых из заданного семейства, то для выделения каждой точки необходимо повторить весь алгоритм сначала (предварительно устранив из рассмотрения точки уже выделенных кривых).

Вероятностное преобразование Хафа (Probabilistic Hough Transform) рассматривает только доля a точек из множества X, при этом результат с некоторой вероятностью получается такой же, как и у стандартного алгоритма. Доля точек выбирается случайно с равномерной вероятностью [15].

Показано, что существует a_threshold такое, что при a > a_threshold ошибок (относительно стандартного алгоритма) происходит очень мало, а при a < a_threshold их количество резко возрастает. Поэтому рекомендуется выбирать a примерно равное a_threshold, которое находится в диапазоне 5% - 15% от всего количества точек.

Очевидное достоинство модификации заключается в сокращении перебора на шаге 2 адаптивного преобразования Хафа. В качестве недостатка можно отметить недетерминированность результата относительно входных данных.

Прогрессивное вероятностное преобразование Хафа (Progressive Probabilistic Hough Transform) состоит в следующем: пусть имеется облако точек X и большое количество точек образуют искомую кривую [11]. Тогда в соответствующей ячейке фазового пространства значение счетчика будет иметь большое значение. Идея этой модификации заключается в том, чтобы выделять кривые (шаг 4) при достижении счетчиком порогового значения, не заполняя аккумулятор полностью (шаг 2). Для вышеописанной кривой значение соответствующего счетчика довольно быстро наберет пороговое значение.

Алгоритм формулируется следующим образом:

а) Если в облаке нет точек, окончание.

б) Аккумулятор пополняется случайно выбранной точкой из множества X, а точка удаляется из рассмотрения.

в) Если максимальное значение аккумулятора не превосходит порога, топереход на шаг 1.

г) Находится кривая максимальной длины.

Внутри некоторого коридора (определяемого ячейкой с максимальным значением счетчика) производится поиск кривой с максимальной длиной.

д) Все точки найденной кривой удаляются с исходного изображения и аккумулятора.

е) Переход на шаг 1.

Достоинством этого метода так же является то, что он постоянно пополняет результат, т.е. его выполнение можно прекратить при достижении остаточного количества результатов или по истечении некоторого времени.

Случайное преобразование Хафа (Randomized Hough Transform) - эта модификация напоминает комбинаторную преобразованию Хафа [15, 17]. Если параметры j кривой F(j,x)=0 можно однозначно восстановить по K точкам, то алгоритм заполнения аккумулятора формулируется следующим образом (шаг 2):

а) Из облака точек X случайным образом выбирается K точек.

б) По выбранным точкам определяются параметры кривой j.

в) Значение счетчика соответствующей ячейки увеличивается.

Перед поиском следующей кривой необходимо удалить из рассмотрения все точки, ассоциированные с предыдущими кривыми, поскольку алгоритм носит случайный характер.

.5 Нахождение точечных особенностей изображения

Особая точка сцены или точечная особенность (point feature) - это такая точка сцены, изображение которой можно отличить от изображений всех соседних с ней точек сцены.

Для сравнения и описания точек можно использовать ее окрестность. Тогда предыдущее определение уточняется следующим образом. Под точечной особенностью понимается такая точка сцены M , лежащая на плоском участке поверхности сцены PlaneSegment, изображение окрестности I(PlaneSegment) которой можно отличить от изображений окрестностей всех других точек сцены N из некоторой другой окрестности этой точки O(M).

Воспользовавшись последним определением можно дать определение точечной особенности изображения:

Точечная особенность изображения m - это такая точка изображения, окрестность которой o(m) можно отличить от окрестности любой другой точки изображения o(n) в некоторой другой окрестности особой точки.