1.2.2 Выделение границ

Перепад - это связное множество пикселей, лежащих на границе между двумя областями. Понятие перепада яркости является "локальным", тогда как граница области, благодаря способу задания, заключает в себе более глобальное представление. Чтобы с уверенностью классифицировать точку как находящуюся на перепаде яркости, изменение яркости, ассоциированное с данной точкой, должно быть существенно большим, чем допустимое изменение яркости в точку фона. Поскольку мы имеем дело с локальными вычислениями, способ определения того, какое значение является "существенным", а какое нет, состоит в установлении порога. Мы определяем точку изображения как точку перепада, если ее двумерная производная первого порядка превышает некоторый порог. Связное множество таких точек есть перепад яркостей. Протяженный перепад яркостей называют контуром. Термин "участок контура" обычно используется, когда протяженность перепада мала по сравнению с размерами изображения [16].

Операторы градиента

Вычисление первой производной цифрового изображения основано на различных дискретных приближениях двумерного градиента[6]. По определению, градиент изображения f(x,y) в точке (x,y) - это вектор вида:

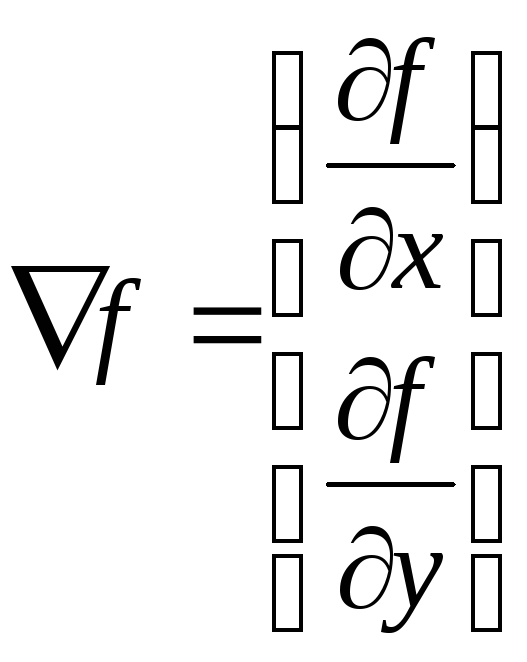
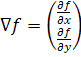,(3)

где ?f/?x, ?f/?y - частные производные по направлениям OX и OY.

Важную роль при обнаружении контуров играет как модуль вектора, так и его направление. Вычисление градиента изображения состоит в получении величин частных производных для каждой точки. Одним из простейших способов нахождения первых производных в точке состоит в применении перекрестного градиентного оператора Робертса, который представляет собой маски, изображенные на рисунке 2.

Рисунок 2 - Маски оператора Робертса

Реализация масок размерами 2?2 неудобна, так как у них нет четко выраженного центрального элемента. С этой целью были разработан оператор Превитта, описываемый масками 3?3 на рисунке 3.

Рисунок 3 - Маски оператора Превитта

Небольшое видоизменение вышеуказанных масок состоит в использовании весового коэффициента для средних элементов. Это увеличенное значение используется для уменьшения эффекта сглаживания за счет придания большего веса средним точкам. Данное видоизменение реализуется при помощи оператора Собела, маски которого изображены на рисунке 4.

Рисунок 4 - Маски оператора Собела

На практике для вычисления дискретных градиентов чаще всего используются операторы Превитта и Собела. Маски оператора Превитта проще реализовать, чем маски оператора Собела, однако у последнего влияние шума угловых элементов несколько меньше, что существенно при работе с производными [7].

Лапласиан

Лапласиан двумерной функции f(x,y) представляет собой производную второго порядка, определяемую выражением:

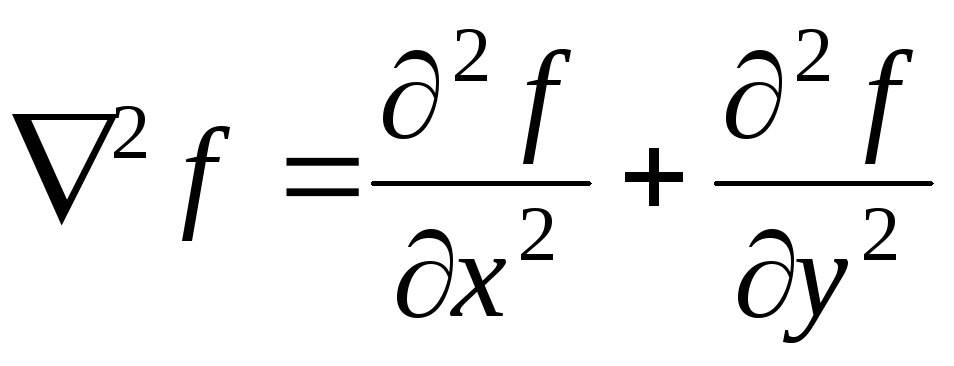
,(4)

где ?²f/?x², ?²f/?y²- частные производные второго порядка.

Для реализации производной второго порядка в дискретном пространстве изображения применяются маски, изображенные на рисунке 5.

Рисунок 5 - Маски лапласиана

Как правило, лапласиан напрямую не используется для обнаружения контуров, что объясняется следующими причинами. Как производная второго порядка, лапласиан является излишне чувствительным к шуму. Кроме того, использование модуля лапласиана приводит к удвоению контуров, что дает нежелательный эффект. Поэтому лапласиан обычно применяют в сочетании со сглаживанием. При использовании функции сглаживания Гаусса выводится маска лапласиана гауссиана [6].

Детектор Канни

Канни досконально исследовал проблему выделения краев различной формы на полутоновом изображении и предложил три критерия, определяющие эффективность детектора края [8]:

1. Хорошее обнаружение, т. е. минимальная вероятность пропуска реального перепада яркости и минимальная вероятность ложного определения перепада (максимизирование выходного отношения сигнал/шум).

2. Хорошая локализация (пиксели, определенные как пиксели края, должны располагаться насколько возможно ближе к центру истинного края).

. Только один отклик на один край.

Вышеперечисленные критерии были записаны в виде уравнений, которые были решены численно, и был определен путем моделирования вид оптимального (в смысле указанных выше критериев) оператора выделения края определенной формы. На рисунке 6 показана свертка изображения с достаточно большой маской, аппроксимирующей оператор [5].

Рисунок 6 - Маска Канни