20

Занятие 3 (Фдз 4).

Отображения множеств. Линейные операторы и их матрицы.

3.1. Отображения множеств. Образ и прообраз. Однозначное и взаимно однозначное отображения, примеры. Обратное отображение. Композиция отображений.

3.2. Линейный оператор, его свойства, примеры линейных операторов.

3.3. Матричная запись действия линейного оператора в заданном базисе. Матрица линейного оператора и ее преобразование при переходе к новому базису.

3.1. Пусть даны два множества и , и задан некоторый закон , по которому каждому элементу из множества ставится в соответствие один или несколько элементов множества . Тогда говорят, что задано отображение (преобразование) множества на множество .

Если отображение ставит в соответствие каждому элементу множества ровно один элемент из множества , то отображение называется однозначным отображением. Пусть элементу отображение ставит в соответствие элемент , тогда принято писать , и элемент называют образом элемента , а элемент - прообразом элемента заданного отображения . Множество всех образов отображения обозначается и называется образом множества .

Если является однозначным отображением множества на множество , и каждый образ имеет только один прообраз , то такое отображение называется взаимно однозначным.

Если даны два однозначных отображения и , то определено однозначное отображение . Отображение называется композицией отображений и .

Если - взаимно однозначное отображение , то существует обратное отображение , действующее по правилу:

.

Композиция отображений является тождественным отображением: .

Пример 1. Пусть - множество, состоящее из трех элементов и - множество, состоящее из пяти элементов .

1) Пусть задано отображение , такое, что .

Закон :

переводит элемент в множество , где состоит из двух элементов ;

переводит элемент в множество ;

переводит элемент в элемент .

Следовательно,

образом элемента является множество ,

образом элемента является множество ,

образом элемента является элемент ,

образом всего множества является множество .

Прообраз элемента состоит из одного элемента ,

прообраз элемента также состоит из одного элемента ,

прообразом элемента служит пустое множество ,

прообраз элемента представляет множество ,

прообраз элемента представляет множество .

Отображение не является однозначным отображением (т.к. образом элемента является не один, а два элемента множества ).

2) Пусть задано отображение , действующее так: .

Здесь :

переводит элемент в элемент (образом элемента является один элемент ); переводит элемент в элемент (образом элемента является один элемент ); переводит элемент в элемент (образом элемента является один элемент );

.

Прообразы элементов - пустые множества.

Прообраз элемента представляет множество из двух элементов .

Прообраз элемента состоит из одного элемента .

Преобразование является однозначным отображением, но не является взаимно однозначным (по двум причинам: прообразы элементов пусты; и прообраз элемента состоит из двух элементов ).

Пример 2. Отображение , где

- множество всех векторов в трехмерном пространстве, - множество всех векторов на плоскости,

. (1)

Найти образ вектора и прообраз вектора .

Решение. Чтобы найти образ подставим координаты вектора в формулы (1):

.

Чтобы найти прообраз вектора , подставим координаты этого вектора в уравнения (1) и решим полученную систему относительно координат .

, .

(Вторая система из первой получена так: к 1-му уравнению прибавили 2-е уравнение и затем переставили местами 2-е и полученное 1-е уравнения).

Таким образом, прообразом вектора служит множество векторов , зависящее от одного параметра .

Приведем примеры взаимно однозначных отображений и обратных им отображений .

1) Пусть ,, . - взаимно однозначное отображение. Обратное отображение действует так:

.

2) Пусть , . Отображение , определенное по правилу , является взаимно однозначным отображением. Обратным отображением будет закон: .

3) Пусть 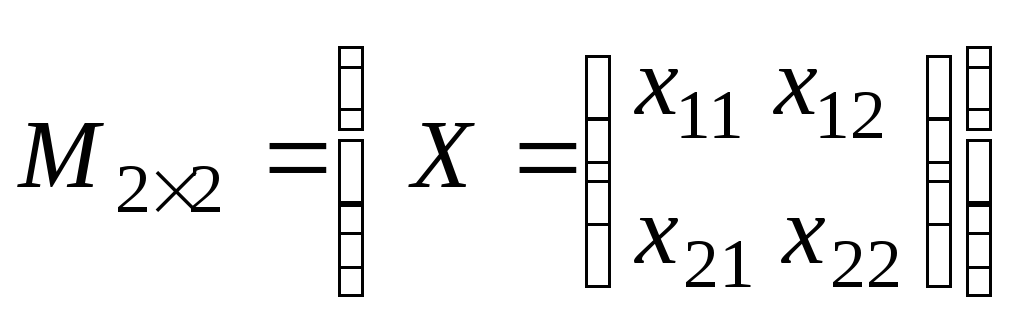- множество всех квадратных матриц второго порядка.

Отображение 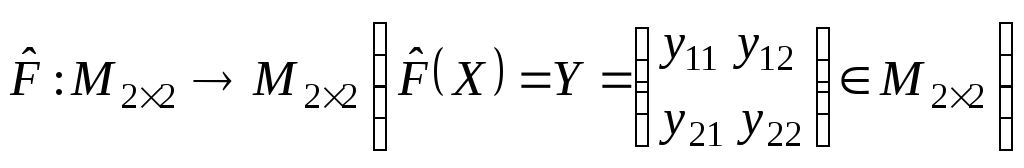, заданное по правилу , где , однозначно определяет по заданной матрице ее образ (матрицу ).

Т.к. определитель матрицы отличен от нуля, то по заданному образу (матрице ) находится ее единственный прообраз – матрица . Следовательно, - взаимно однозначно отображает множество на множество. Обратное отображение действует так: .

Пример 3., , . Даны два однозначных отображения

и .

Найти отображение - композицию отображений и .

Решение.

Согласно определению композиции отображений имеем:

; ; ;

. Следовательно, - множество из трех элементов .