2.Расчёт неизвестных токов по законам Кирхгофа

Число неизвестных токов – 7, число узлов a,b,c,d,m равно 5, число уравнений по I закону Кирхгофа должно быть 5-1=4, так как один из узлов заземлен. Для составления уравнений по II закону Кирхгофа нужно 7-4=3 уравнения. Составляем граф схемы (источники энергии в графе представляем своими внутренними сопротивлениями , резисторы R не изображаются) рис.3.

Рис.3.Ненаправленный граф схемы 2

Решая систему, находим неизвестные токи I1, I2, I3, I4, I5, I6, IR2.

Методом компьютерного моделирования были найдены значения неизвестных токов: I1=0.489, I2=0.688, I3=1.193, I4=1.177, I5=0.016, I6=0.704 IR2=0.988. Подставив их в систему уравнений, проверяем правильность её составления:

0.688+0.016=0.704; 0.704=0.704

1.193=1.177+0.016; 1.193=1.193

0.704+0.489=1.193; 1.193=1.193

0.688+0.3=0.988; 0.988=0.988

0.704*7.5+1.193*6+0.016*4=12.5; 12.5=12.5

-1.193*6-1.177*3.5-0.489*2.5=-12.5; -12.5=-12.5

1.177*3.5+0.988*5-0.016*4=9; 9=9

2.Расчёт неизвестных токов в ветвях МКТ

Число уравнений системы МКТ равно число уравнений по II закону Кирхгофа. В контурах I, II, III протекают неизвестные контурные токи I₁₁, I₂₂, I₃₃, которые и являются неизвестными системы. В ветви с источником тока течет известный ток J₂, который создает в ячейке известный контурный ток J₂₂=J₂=0,3 A (схема 2) рис. 5.

Рис.5.Контурные токи

в схеме 2

перенесём J22R2=J2R2=Eэ в правую часть:

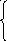
э

В таком виде система соответствует схеме 3. Запишем систему в матричной форме:

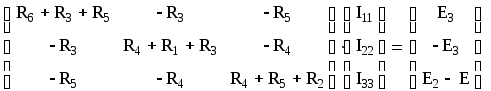
Матрица в числах:

Решая систему относительно неизвестных контурных токов, находим I11=0.704 A, I22=-0.489 A, I33=0.688 A и по принципу наложения выражаем через них токи в ветвях:

I6= I11=0.704 A I3=I11-I22=1,193 A

I1=-I22=0.489 A I4=I33-I22=1.177 A

I2=I33=0.688 A I5=I11-I33=0.016 A

Методом компьютерного моделирования были найдены значения неизвестных контурных токов, которые равны I11= 0.704 A, I22=-0.489 A, I33=0.688 A.

3. Расчёт неизвестных токов в ветвях МУП

Число уравнений системы равно числу уравнений по I закону Кирхгофа. Неизвестными системы являются неизвестные потенциалы узлов. Потенциал одного из узлов примем равным 0. В схеме, где есть ветвь, содержащая только Е, нужно выбирать за нуль потенциал одного из узлов этой ветви.

Для схемы 2: φa= 0 , =φa +E₂=9 B.

Неизвестными будут φb, и .

Для схемы 3:

Системы эквивалентны, так как

Система в матричной форме:

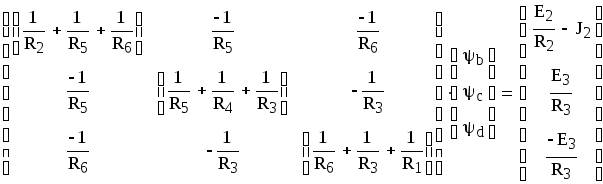
Решая систему относительно неизвестных, находим неизвестные потенциалы узлов:

φb=4.057 В, =4.120 В, =-1.222 В.

Выражаем токи в ветвях по закону Ома:

По схеме 2:

По схеме 3:

Методом компьютерного моделирования были найдены значения неизвестных потенциалов:φb=4.057 B, φd=-1.222 B, φc=4.120 B, φm=9 B. Подставив их в систему уравнений, проверяем правильность её составления:

Сравнительная таблица результатов расчёта токов

	А	А	А	А	А	А	А
МКТ	0,489	0,688	0,988	1,193	1,177	0,016	0,704
МУП	0,489	0,688	0,988	1,193	1,177	0,016	0,704

4. Баланс мощностей (в схеме 2)

5.Методом компьютерного моделирования для схемы 3 были найдены неизвестные токи: I1=0.489 А, I2=0.688 A, I3=1.193 A, I4=1.177 A, I5=0.016 A, I6=0.704 A. Эти значения совпадают со значениями сил тока для схемы 2, рассчитанных в п.1.