6. Синтез цифровых схем. Переход от таблицы истинности логического устройства к структурной формуле и схеме цифрового устройства. Преобразование логических функций

Как мы видели выше, любую булеву функцию можно представить либо в виде таблицы истинности, либо в виде алгебраического уравнения. В алгебраической форме функцию удобно преобразовывать, например, с целью ее минимизации, т.е. получения наиболее простой формы. Существуют две формы функций в алгебраическом виде, называемые нормальными.

Первая форма – дизъюнктивная нормальная форма, представляет собой логическую сумму элементарных логических произведений, в каждое из которых аргумент или его отрицание входит не более одного раза. Например:

Если каждое слагаемое содержит все переменные или их отрицания, имеем первую стандартную форму или совершенную дизъюнктивную форму. Например:

Вторая форма или конъюнктивная нормальная форма есть логическое произведение элементарных логических сумм. Если каждая сумма содержит все переменные или их отрицания, имеем вторую стандартную форму или совершенную конъюнктивную форму. Например:

При переходе от таблицы к алгебраической записи всегда получается первая или вторая стандартные формы, однако, после преобразований форма записи может быть произвольной.

Переход от таблицы истинности к первой стандартной форме осуществляется следующим образом. Для каждого набора аргументов, на котором функция равна единице, записывается произведение всех аргументов, причем, если аргумент в этом наборе принимает значение 0, то пишется его отрицание. Затем производится логическое сложение этих элементарных произведений.

Для наглядности рассмотрим две функции ИЛИ и И. Их таблицы истинности представлены ниже.

Функция ИЛИ			Функция И
х1	х2	F(x1,x2)	x1	x2	F(x1,x2)
0	0	0	0	0	0
0	1	1	0	1	0
1	0	1	1	0	0
1	1	1	1	1	1

Уравнение в первой стандартной форме для функции ИЛИ:

(1)

Для функции И:

(2)

Иногда эту процедуру называют составлением структурной формулы по единицам.

Для перехода ко второй стандартной формуле необходимо:

Для каждого набора аргументов, на котором функция равна 0, составить элементарную сумму, причем если аргумент в этом наборе принимает значение 1, то пишется его отрицание. Затем эти элементарные суммы объединяются операцией логического умножения.

Уравнение во второй стандартной форме для функции ИЛИ:

(3)

Для функции И:

(4)

Уравнения 2 и 3 не требуют преобразований. Это их минимальная форма. Уравнения 1 и 4 могут быть преобразованы. Заметим, кстати, что уравнения 1 и 3, 2 и 4 записаны соответственно для функции ИЛИ и И, следовательно, должны быть тождественными:

Пользуясь теоремами булевой алгебры преобразуем уравнение 1. Воспользуемся правилом повторения , правилом отрицания

Для преобразования уравнения 4 применим к нему принцип двойственности:

Если

то

И далее, аналогично предыдущему:

Еще раз применим принцип двойственности и получим окончательно:

Процедура построения схемы по заданному уравнению достаточно проста. Схема строится в той же последовательности, как происходит вычисление функции. Необходимо учитывать приоритет операций: отрицание, умножение, сложение. Схема должна иметь столько входов, сколько у функции аргументов, и один выход, соответствующий самой функции. На входы подаются сигналы, соответствующие аргументам. Если кроме аргументов в уравнении есть отрицания аргументов, то для их получения в схеме применяют элементы НЕ. Для умножения используются элементы И, для сложения – ИЛИ. Для примера построим схемы по уравнениям 1 и 4.

Схема по уравнению 1:

(рис. 18а) будет состоять из двух элементов НЕ для получения отрицаний и, трех двухвходовых элементов И для реализации произведений аргументови одного трехвходового элемента ИЛИ для получения окончательной суммы трех произведений. Схема по уравнению 4:

(рис. 18б) будет состоять из двух элементов НЕ, трех элементов ИЛИ и одного элемента И.

Рис. 18. Схемы построенные по уравнению 1 (а) и 4 (б)

Построенные нами схемы представляют соответственно элементы ИЛИ и И. Ясно, что перед тем как строить схему, уравнение нужно упростить, т.е. минимизировать. Результат минимизации неоднозначен, и одной заданной таблице истинности могут соответствовать различные схемы.

Рассмотрим для примера функцию неравнозначности (ИСКЛЮЧАЮЩЕЕ ИЛИ). Ее таблица истинности следующая:

ИСКЛЮЧАЮЩЕЕ ИЛИ
x1	x2	F(x1,x2)
0	0	0
0	1	1
1	0	1
1	1	0

Уравнение по первой стандартной форме:

(5)

Уравнение по второй стандартной форме:

(6)

Преобразуем вторую скобку в уравнении 6 по принципу двойственности:

(7)

Рис. 19. Схемы по уравнениям 5 (а) и 7 (б)

Для построения схемы по уравнению 5 необходимы 2 элемента НЕ, два двухвходовых элемента И и один двухвходовый элемент ИЛИ. В схеме, построенной по уравнению 7 на один элемент НЕ меньше (рис. 19).

Как было отмечено выше, существуют полные наборы логических функций, к которым относятся три функции ИЛИ, И, НЕ, функция ИЛИ-НЕ, функция И-НЕ. Все построенные нами схемы использовали полный набор функций ИЛИ, И, НЕ. Однако представляет интерес и имеет практическое значение использование для построения схем базовых логических элементов ИЛИ-НЕ и И-НЕ. Как, например, построить схему элемента ИСКЛЮЧАЮЩЕЕ ИЛИ имея только элементы ИЛИ-НЕ или И-НЕ? Для построения этой схемы на элементах ИЛИ-НЕ (рис. 20а) воспользуемся уравнением 6. Преобразуем его по принципу двойственности:

Для построения схемы на элементах И-НЕ (рис. 20б) преобразуем уравнение 5, избавляясь от операции логического сложения:

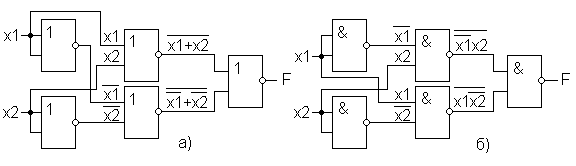
Рис. 20. Схемы элемента ИСКЛЮЧАЮЩЕЕ ИЛИ на элементах ИЛИ-НЕ (а) и И-НЕ (б)

Вопросы для самопроверки

6.1. Сформулируйте правило перехода от таблицы истинности к первой стандартной форме. Приведите примеры. Запишите уравнение функции равнозначности в первой стандартной форме.

6.2. . Сформулируйте правило перехода от таблицы истинности ко второй стандартной форме. Приведите примеры. Запишите уравнение функции неравнозначности во второй стандартной форме.

6.3. Докажите, что уравнения функции ИСКЛЮЧАЮЩЕЕ ИЛИ, записанные в первой и второй стандартных формах преобразуются одна в другую.

6.4. Постройте схему устройства, описываемого уравнением, полученным в пункте 6.1.

6.5. Постройте схему элемента ИЛИ на элементах И-НЕ.

6.6. Постройте схему элемента И на элементах ИЛИ-НЕ.

6.7. Постройте схему элемента реализующего функцию равнозначности на элементах И-НЕ.

6.8. Постройте схему элемента реализующего функцию равнозначности на элементах ИЛИ-НЕ.

6.9. Постройте схему элемента ИСКЛЮЧАЮЩЕЕ ИЛИ на элементах И, ИЛИ, НЕ.

6.10. Используя таблицу истинности RS-триггера, запишите уравнения для прямого и инверсного выходов и минимизируйте их. Сравните с уравнениями в разделе 4.