7.1.2 Тела вращения

Телами вращения называют тела, ограниченные либо поверхностью вращения, либо поверхностью вращения и плоскостью (рисунок 134). Под поверхностью вращения понимают поверхность, полученную от вращения какой-либо линии (ABCDE), плоской или пространственной, называемой образующей, вокруг неподвижной прямой (i) — оси вращения.

Рисунок 134

Любая точка образующей поверхности вращения описывает окружность, расположенную в плоскости, перпендикулярной к оси вращения – параллель, следовательно, плоскость, перпендикулярная к оси вращения, всегда пересекается с поверхностью вращения по окружности. Наибольшая параллель — экватор. Наименьшая параллель — горло (горловина).

Плоскости, проходящие через ось вращения, называют меридиональными плоскостями.

На комплексном чертеже изображение тел вращения выполняется посредством изображения ребер оснований и линий очерков поверхности.

Линии пересечения меридиональных плоскостей с поверхностью называют меридианами.

Меридиональная плоскость, параллельная плоскости проекций, называется главной меридиональной плоскостью. Линия ее пересечения с поверхностью — главный меридиан.

Прямой круговой цилиндр.Прямым круговым цилиндром (рисунок 135) называют тело, ограниченное цилиндрической поверхностью вращения и двумя кругами — основаниями цилиндра, расположенными в плоскостях, перпендикулярных к оси цилиндра.Цилиндрической поверхностью вращенияназывается поверхность, полученная при вращении прямолинейной образующейAA₁вокруг параллельной ей неподвижной прямой -i(ось вращения). Размерами, характеризующими прямой круговой цилиндр, являются его диаметрDци высотаl(расстояние между основаниями цилиндра).

а б в

Рисунок 135

Прямой круговой цилиндр можно также рассматривать как тело, полученное при вращении какого-либо прямоугольника ABCD вокруг одной из его сторон, например, ВС (рисунок 136). Сторона ВС является осью вращения, а сторона AD — образующей цилиндра. Две другие стороны обозначат основания цилиндра.

Рисунок 136

Прямоугольника АВ и CD при вращении образуют круги — основания цилиндра.

Построение проекций цилиндра.

Построение горизонтальной и фронтальной проекций цилиндра начинают с изображения основания цилиндра, т. е. двух проекций окружности (см. рисунок 135, б). Так как окружность расположена на плоскости Н, то она проецируется на эту плоскость без искажения. Фронтальная проекция окружности представляет собой отрезок горизонтальной прямой линии, равный диаметру окружности основания.

После построения основания на фронтальной проекции проводят две очерковые образующие (крайние образующие) и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, который является фронтальной проекцией верхнего основания цилиндра (рисунок 135, в).

Определение недостающих проекций точек А и В, расположенных на поверхности цилиндра, по заданным фронтальным проекциям в данном случае затруднений не вызывает, так как вся горизонтальная проекция боковой поверхности цилиндра представляет собой окружность (рисунок 137, а). Следовательно, горизонтальные проекции точек А и В можно найти, проводя из данных точек A'' и B'' вертикальные линии связи до их пересечения с окружностью в искомых точках A' и B'.

Профильные проекции точек А и В строят также при помощи вертикальных и горизонтальных линий связи.

Изометрическую проекцию цилиндра вычерчивают, как показано на рисунок 137, б.

В изометрии точки А и В строят по их координатам. Например, для построения точки В от начала координат О по оси x откладывают координату ∆x, а затем через ее конец проводят прямую, параллельную оси у, до пересечения с контуром основания в точке 2. Из этой точки параллельно оси z проводят прямую, на которой откладывают координату Z_B, точки В.

а б

Рисунок 137

Прямой круговой конус.Прямым круговым конусом (рисунок 138) называют тело, ограниченное конической поверхностью вращения и кругом, расположенным в плоскости, перпендикулярной к оси конуса.Коническая поверхностьполучается при вращении прямолинейной образующейSA(рисунок 138, а), проходящей через неподвижную точкуSна оси вращенияiи составляющей с этой осью некоторый постоянный угол. ТочкаSназываетсявершиной конуса, а коническая поверхность — боковой поверхностью конуса. Размер прямого кругового конуса характеризуют диаметр его основанияD_Kи высотаН.

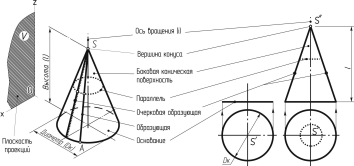
а) б) в)

Рисунок 138

Прямой круговой конус можно также рассматривать как тело, полученное при вращении прямоугольного треугольника SAB вокруг его катета SB (рисунок 139). При таком вращении гипотенуза описывает коническую поверхность, а катет АВ — круг, т. е. основание конуса.

Рисунок 139

Построение проекций конуса.

Последовательность построения двух проекций конуса показана на рисунке 167, б и в. Сначала строят две проекции основания. Горизонтальная проекция основания — окружность. Фронтальной проекцией будет отрезок горизонтальной прямой, равный диаметру этой окружности (рисунок 138, б). На фронтальной проекции из середины основания восставляют перпендикуляр, и на нем откладывают высоту конуса (рисунок 138, в). Полученную фронтальную проекцию вершины конуса соединяют прямыми с концами фронтальной проекции основания и получают фронтальную проекцию конуса.

Построение точек на поверхности конуса

Если на поверхности конуса задана одна проекция точки А (например, фронтальная проекция на рисунке 140), то две другие проекции этой точки определяют с помощью вспомогательных линий — образующей, расположенной на поверхности конуса и проведенной через точку А, или окружности, расположенной в плоскости, параллельной основанию конуса.

а б в

Рисунок 140

В первом случае (рисунок 140, а) через точку A проводят фронтальную проекцию 1''S'' вспомогательной образующей. Пользуясь вертикальной линией связи, проведенной из точки 1, расположенной на фронтальной проекции окружности основания, находят горизонтальную проекцию 1' этой образующей, на которой при помощи линии связи, проходящей через A', находят искомую точку A.

Во втором случае (рисунок 140, б) вспомогательной линией, проходящей через точку А, будет окружность, расположенная на конической поверхности и параллельная плоскости Н - параллель. Фронтальная проекция этой окружности изображается в виде отрезка 1''1'' горизонтальной прямой, величина которого равна диаметру вспомогательной окружности. Искомая горизонтальная проекция A' точки А находится на пересечении линии связи, опущенной из точки A', с горизонтальной проекцией вспомогательной окружности.

Если заданная фронтальная проекция 1'' точки 1 расположена на контурной (очерковой) образующей, то горизонтальная проекция точки находится без вспомогательных линий.

В изометрической проекции точку А, находящуюся на поверхности конуса, строят по трем координатам (см. рисунок 140, в): X, Y и Z_А. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от точки О по оси х отложена координата X; из конца ее параллельно оси у проведена прямая, на которой отложена координата Y; из конца отрезка, параллельно оси z проведена прямая, на которой отложена координата Z_А. В результате построений получим искомую точку А.

Шар.Шаром (рисунок 141) называют тело, полученное при вращении полукругаABC(образующая) вокруг его диаметраАС (ось вращения), а поверхность, которую при этом описывает дугаABC, называется шаровой или сферической. Шар относится к телам, ограниченным только поверхностью вращения.

Рисунок 141

Шаровая (сферическая) поверхность является геометрическим местом точек, равноудаленных от одной точки О, называемой центром шара. Если шар рассечь горизонтальными плоскостями, то в сечении получатся окружности – параллели. Наибольшая из параллелей имеет диаметр равный диаметру шара. Такая окружность называется экватором. Окружности же, получаемые в результате сечений шара плоскостями, проходящими через его ось вращения, называются меридианами.

Построение проекций шара и точек на его поверхности

Проекции шара приведены на рисунке 142, а. Горизонтальная и фронтальная проекции — окружности радиуса, равного радиусу сферы.

а б

Рисунок 142

Если точка А расположена на сферической поверхности, то вспомогательная линия 1'' 2'', проведенная через эту точку параллельно оси Ох (параллель), проецируется на горизонтальную плоскость проекций окружностью. На горизонтальной проекции вспомогательной окружности находят с помощью линии связи искомую горизонтальную проекцию A' точки А.

Величина диаметра вспомогательной окружности равна фронтальной проекции 1''2''.

Аксонометрическое изображение сферы (шара) выполняется в виде окружности (рисунок 142 б), радиус которой геометрически определяется как расстояние от центра сферы до проекции экватора (эллипса) вдоль большей ее оси (перпендикулярной Oz).

В аксонометрической проекции точку А, находящуюся на поверхности шара, строят по трем координатам: X_А, Y_А и Z_А. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям. В рассматриваемом примере от точки О по оси х отложена координата X_А; из конца ее параллельно оси у проведена прямая, на которой отложена координата Y_А; из конца отрезка, параллельно оси z проведена прямая, на которой отложена координата Z_А. В результате построений получим искомую точку А.

Тор– тело (рисунок 143), образованное вращением окружности или ее дуги вокруг оси, расположенной в одной с ней плоскости но не проходящей через центр окружности или ее дуги.

а б

Рисунок 143

Если ось вращения не пересекает образующую окружность, то тор называют кольцом (открытый тор) (рисунок 143, а). Если же ось вращения пересекает образующую окружность, то получается торовая поверхность бочкообразном формы (закрытый тор или пересекающийся тор) (рисунок 143, б). В последнем случае образующей торовой поверхности является дуга ABC окружности.

Наибольшую из окружностей, которые описывают точки образующей торовой поверхности, называют экватором, а наименьшую — горлом, или горловиной.

Построение проекций тора

Круговое кольцо (или открытый тор) имеет горизонтальную проекцию в виде двух концентрических окружностей, разность радиусов которых равна толщине кольца или диаметру образующей окружности (рисунок 145). Фронтальная проекция ограничивается справа и слева дугами полуокружностей диаметра образующей окружности.

На рисунке 144, а и б приведены два вида закрытого тора. В первом случае образующая дуга окружности радиуса R отстоит от оси вращения на расстоянии меньше радиуса R, а во втором случае — больше. В обоих случаях фронтальные проекции тора представляют собой действительный вид двух образующих дуг окружности радиуса R, расположенных симметрично по отношению к фронтальной проекции оси вращения. Профильными проекциями тора будут окружности.

а б

Рисунок 144

Построение точек на поверхности тора

В случае, когда точка А лежит на поверхности кругового кольца и дана одна ее проекция, для нахождения второй проекции этой точки применяется вспомогательная окружность, проходящая через данную точку А и расположенная на поверхности кольца в плоскости, перпендикулярной оси кольца (рисунок 145).

Если задана фронтальная проекция A'' точки А, лежащей на поверхности кольца, то для нахождения ее второй проекции (в данном случае — горизонтальной) через A" проводят фронтальную проекцию вспомогательной окружности — отрезок горизонтальной прямой линии 2''2''. Затем строят горизонтальную проекцию 2'2' этой окружности и на ней, применяя линию связи, находят точку A'.

Если задана горизонтальная проекция B' точки B, расположенной на поверхности этого кольца, то для нахождения фронтальной проекции этой точки через 1' проводят горизонтальную проекцию вспомогательной окружности радиуса R₁. Затем через левую и правую точки 1' и 1' этой окружности проводят вертикальные линии связи до пересечения с фронтальными проекциями очерковой образующей окружности радиуса R и получают точки 1'' и 1''. Эти точки соединяют горизонтальной прямой, которая представляет собой фронтальную проекцию вспомогательной окружности (она будет видима). Проводя вертикальную линию связи из точки B' до пересечения с прямой 1''1'' получаем искомую точку B''.

Такие же приемы построения применимы и для точек, находящихся на поверхности тора.

Рисунок 145

Построение аксонометрического изображения тора можно разделит на три этапа (рисунок 146). Сначала строится в виде эллипса проекция радиальной осевой линии (траектория движения центра образующей окружности). Затем определяем радиус сферы, касающейся тора по образующей (окружности). Для этого строим в виде меньшего эллипса проекцию фронтальной очерковой образующей тора. Радиус сферы определим как длину отрезка О₁F от центра эллипса до точки на этом эллипсе, лежащей на большой оси эллипса (перпендикулярной Oy). Далее строим большое количество окружностей радиусом R_сферы с центрами на проекции радиальной осевой тора О_{1 …} О_n (чем больше, тем точнее контур будущего тора). В завершение проводим линию контура тора как линию, касающуюся каждой окружности сферы.

а б

Рисунок 146

В аксонометрической проекции точку А, находящуюся на поверхности тора, строят по трем координатам: X_А, Y_А и Z_А. Эти координаты последовательно откладывают по направлениям, параллельным изометрическим осям.