7 Геометрические тела
7.1 Понятие о простейших геометрических телах
В разделе проекционного черчения изучаются способы изображения на плоскости объемных тел. Телом называют часть пространства, ограниченную со всех сторон поверхностями. Телами являются все предметы, окружающие нас. По форме они очень разнообразны. Однако при внимательном анализе можно убедиться в том, что большинство из них образовано сочетанием простейших геометрических тел, таких как многогранники (призма и пирамида) и тела вращения прямые круговые (цилиндр и конус, шар и тор).
7.1.1 Многогранники
Многогранником называют геометрическое тело, ограниченное плоскими многоугольниками — гранями (рисунок 126). Стороны граней называют ребрами, а концы ребер — вершинами. Чаще всего встречаются многогранники двух видов — призмы и пирамиды.
На комплексном чертеже изображение многогранников выполняется посредством изображения ребер каркаса поверхности.
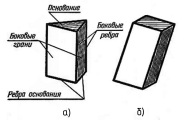
Рисунок 126
Призма. Призмой называют многогранник, у которого две грани — основания призмы — равные многоугольники, расположенный в параллельных плоскостях, а остальные грани, называемые боковыми, параллелограммы. Призмы бывают прямые и наклонные. Прямой призмой называют призму (рисунок 126, а), у которой боковые грани перпендикулярны к ее основанию. У наклонной призмы боковые грани составляют с основанием острые углы (рисунок 126, б).
По числу боковых граней призмы различают на трехгранные, четырехгранные и т. д.
Построение проекций правильной прямой шестиугольной призмы
Построение проекций правильной прямой призмы (рисунок 127) начинается с выполнения ее горизонтальной проекции — правильного шестиугольника. Из вершин этого шестиугольника проводят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы. Так как основание призмы параллельно горизонтальной плоскости проекций H, то эта проекция изображается отрезком прямой параллельно оси OX. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер — отрезки вертикальных прямых, равные высоте призмы. Фронтальные проекции передних и задних ребер совпадают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых (т.к. они перпендикулярны горизонтальной плоскости проекций). Передняя боковая грань 1243 изображается на фронтальной плоскости проекций V без искажения, а на плоскости H — в виде прямой линии. Фронтальные и профильные проекции остальных граней изображаются с искажением.
Рисунок 127
На чертеже оси х, у и z не показывают, что делает чертеж более простым.
Построение проекций наклонной призмы.
Рассмотрим порядок построения проекций наклонной шестиугольной призмы в двух различных положениях ее по отношению к плоскости Н.
1. Наклонная шестиугольная призма, основание которой лежит на плоскости Н, наклонённой к ней под углом α (рисунок 128). Ребра призмы параллельны плоскости V, т. е. являются фронталями.
Вначале выполняется построение горизонтальной проекции основания призмы, которое проецируется на плоскость Н без искажения (правильный шестиугольник). Фронтальная проекция основания представляет собой отрезок прямой, параллельной оси х.
Из точек 1', 2', 3', 4' фронтальной проекции основания проводят прямые проекции ребер под углом α к оси х и на них откладывают действительную длину бокового ребра призмы.
Строят фронтальную проекцию верхнего основания призмы в виде отрезка прямой, равного и параллельного фронтальной проекции нижнего основания.
Рисунок 128
Из точек 1', 2', 3', 4', 5', 6' горизонтальной проекции нижнего основания проводят прямые — проекции ребер — параллельно оси х и на них при помощи вертикальных линий связи находят шесть точек — горизонтальные проекции вершин верхнего основания призмы.
2. Прямая правильная шестиугольная призма наклонена под углом α к плоскости Н. Основание призмы наклонено к плоскости Н под углом β (рисунок 129).
Рисунок 129
В этом случае необходимо вначале построить фронтальную проекцию основания. Эта проекция представляет собой отрезок, равный расстоянию между параллельными сторонами шестиугольника. Если этот отрезок разделить пополам и из его середины провести линию связи, то на ней будут расположены точки 2' и 5' — горизонтальные проекции вершин основания призмы. Расстояние между точками 2', 5' равно действительному расстоянию между вершинами основания призмы. Так как горизонтальные проекции сторон 1'6' и 3'4' представляют собой их действительные длины, то, воспользовавшись этим обстоятельством, можно построить полностью горизонтальную проекцию основания.
Дальнейший процесс построения, показанный на рисунке 129, аналогичен приведенному на рисунке 128.
Построение проекций точки на поверхности призмы по известной одной ее проекции
Пример.
Дан комплексный чертеж четырехугольной прямой призмы и фронтальная проекция А'' точки А (рисунок 130).
Прежде всего, надо отыскать на комплексном чертеже две проекции грани, на которой расположена точка А. На комплексном чертеже видно (рисунок 163, а), что точка А лежит на грани призмы 1265.
Рисунок 130
Фронтальная проекция А'' точки А лежит на фронтальной проекции 1''2''6''5'' грани призмы. Горизонтальная проекция 1'5'6'2' этой грани — отрезок 56. На этом отрезке и находится горизонтальная проекция A' точки А. Профильную проекцию призмы и точки А строят, применяя линии.
По имеющемуся комплексному чертежу призмы можно выполнить ее аксонометрию по координатам вершин. Для этого вначале строят нижнее основание призмы (рисунок 131, а), а затем - вертикальные ребра и верхнее основание (рисунок 131, б).
а б
Рисунок 131
По координатам точки А, взятым с комплексного чертежа, можно построить аксонометрическую проекцию этой точки.
Пирамида.Пирамидой называют многогранник (рисунок 132, а), в основании которого плоский многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов многоугольника основания пирамиды бывают треугольные, четырехугольные и т.д. Если пирамида усечена плоскостью, параллельной ее основанию, то ее называют усеченной (рисунок 132, б).
а б
Рисунок 132
Построение проекции треугольной пирамиды
Построение проекции треугольной пирамиды начинается с построения основания, горизонтальная проекция которого представляет собой треугольник без искажения (рисунок 133, а). Фронтальная проекция основания — отрезок горизонтальной прямой.
Из горизонтальной проекции точки S' (вершины, пирамиды) проводят вертикальную линию связи, на которой от оси х откладывают высоту пирамиды и получают фронтальную проекцию вершины. Соединяя точку с точками 1'', 2'' и 3'', получают фронтальные проекции ребер пирамиды.
Горизонтальные проекции ребер получают, соединяя горизонтальную проекцию точки S' с горизонтальными проекциями точек 1', 2' и 3'.
Построение точки на поверхности пирамиды
Пример.
Пусть, например, дана фронтальная проекция А'' точки А, расположенной на грани пирамиды 1S2, и требуется найти другую проекцию этой точки.
Первый способ. Для решения этой задачи проведем через A'' вспомогательную прямую любого направления и продолжим ее до пересечения с фронтальными проекциями 1''S'' и 2''S'' ребер в точках N'' и M''. Затем проведем из точек N'' и M'' линии связи до пересечения с горизонтальными проекциями 1'S' и 2'S' этих ребер. Соединив точки, получим горизонтальную проекцию вспомогательной прямой, на которой с помощью линии связи найдем искомую горизонтальную проекцию A' точки А. Профильную проекцию этой точки находят по линиям связи.
Другой способ решения задачи на построение проекции точки по заданной ее проекции показан на 133, а. Дана треугольная пирамида. Через заданную фронтальную проекцию A'' точки А проводят вспомогательную прямую, проходящую через вершину пирамиды и расположенную на ее грани точку ребра основания F, . Горизонтальную проекцию F'S' вспомогательной прямой находят, применяя линию связи. Искомая горизонтальная проекция А' точки А находится на пересечении линии связи, проведенной из точки A'', с горизонтальной проекцией F'S' вспомогательной прямой.
Если необходимо определить положение точки на ребре, совпадающем с линий связи, без третей проекции, проводят вспомогательную прямую через точку параллельно соответствующему отрезку основания (рисунок 133 б). Определение положения точки В на горизонтальной плоскости проекций, лежащей на ребре S2, начинается с проведения через фронтальную проекцию В'' точки В линии параллельной линии основания 23 до пересечения с ребром пирамиды S3. Строим горизонтальную проекцию точки пересечения вспомогательной линии и ребра S3 точку С, опуская линию связи на горизонтальную проекцию ребра S'3'. Из точки С' параллельно линии 1'3' провидим горизонтальную проекцию вспомогательной линии до пересечения с линией связи от фронтальной проекции А'' точки А.
Аксонометрическая проекция пирамиды выполняется следующим образом (рисунок 133, б).
а б
Рисунок 133
Вначале строят основание, для чего каждую вершину основания строят по координатам, откладывая их вдоль оси OY и OX соответственно. Из точки О проводят ось z и на ней откладывают высоту пирамиды. Вершину S соединяют с вершинами основания прямыми линиями — ребрами.
Аксонометрическую проекцию точки С, расположенной на грани пирамиды, строят по координатам, которые берут с комплексного чертежа. От начала координат О по оси х откладывают координату XС, из ее конца параллельно оси у — половину координаты YС и из конца этой координаты параллельно оси z — третью координату ZС. Построение точки В, расположенной на ребре пирамиды, более простое. От точки О по оси х откладывают координату XB и из конца се проводят прямую, параллельную оси z, до пересечения с ребром пирамиды в точке В.