4.2 Лекальные кривые

Лекальные кривые– это такие кривые, которые могут быть вычерчены только с помощью лекала по предварительно построенным точкам. Лекальные кривые широко применяются в очертаниях различных деталей и предметов. Это могут быть профили зубчатых колес и кулачков, очертания кронштейнов, подвесок, посуды и мебели. Лекальные кривые могут быть также получены в результате сечения цилиндра, конуса и других тел вращения плоскостью.

4.2.1 Порядок вычерчивания лекальных кривых

Пусть на рисунке 64, а заданы точки 1,2, ..., 11, принадлежащие некоторой кривой. Предварительно эти точки от руки с помощью мягкого карандаша соединяют тонкой, по возможности более плавной кривой линией (рисунок 64, б). Желательно, чтобы расстояние между точками лекальной кривой не превышало 15 мм. Если же две соседние точки кривой расположены далеко друг от друга и характер кривой не совсем ясен, то следует построить дополнительно еще одну или две точки.

а б в г

Рисунок 64

Затем приступают к предварительной обводке кривой с помощью лекала. Лекало надо подобрать такое, чтобы очертания некоторых его участков были похожи на отдельные участки данной кривой. Предварительный подбор лекала рекомендуется делать на длину всей кривой и черточками на нем помечать выбранные участки. Это особенно важно для обводки симметричных кривых, таких, как эллипс, парабола и др.

Подобранное лекало прикладывают к кривой так, чтобы лежащие подряд как минимум три или четыре точки кривой совпали с определенным участком лекала (например, точки 1–5на рисунке 64, б). Далее подбирают следующий участок лекала таким образом, чтобы он охватывал также три или четыре точки кривой, включая хотя бы одну точку из предыдущего участка (например, точки4–9на рисунке 64, в). Благодаря такому перекрытию двух соседних участков достигается плавность кривой. После того, как будут подобраны участки лекала на протяжении всей кривой, приступают к окончательной обводке ее карандашом или тушью Обводку следует начинать с места наиболее крутого изгиба кривой. На каждом участке обводят среднюю часть его, включая половину участков перекрытия. Такая обводка обеспечивает наибольшую плавность кривой (рисунок 64, г).

4.2.2 Способы построения некоторых лекальных кривых

Эллипс.Если рассечь поверхность кругового конуса наклонной плоскостьюРтак, чтобы она пересекла все его образующие, то в плоскости сечения получится эллипс (рисунок 65).

Рисунок 65

Эллипс(рисунок 66) – плоская замкнутая кривая, у которой сумма расстояний от любой ее точки (например, от точкиМ) до двух заданный точекF₁ и F₂ – фокусов эллипса – есть величина постоянная, равная длине его большой оси AB (например, F₁M + F₂M = AB). Отрезок AB называется большой осью эллипса, а отрезок CD – его малой осью. Оси эллипса пересекаются в точке O – центре эллипса, а его размер определяет длины большой и малой осей. Точки F₁ и F₂ расположены на большой оси AB симметрично относительно точки O и удалены от концов малой оси (точек С и D) на расстояние, равное половине большой оси эллипса .

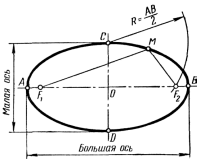
Рисунок 66

Существует несколько способов построения эллипса. Наиболее просто построить эллипс по двум его осям при помощи вспомогательных окружностей (рисунок 67). В этом случае задают центр эллипса – точку O и через нее проводят две взаимно перпендикулярные прямые (рисунок 67, а). Из точки О описывают две окружности радиусами, равными половине большой и малой осей. Большую окружность делят на 12 равных частей и точки деления соединяют с точкой О. Проведенные линии разделят меньшую окружность также на 12 равных частей. Затем через точки деления меньшей окружности проводят горизонтальные прямые (или прямые, параллельные большой оси эллипса), а через точки деления большей окружности – вертикальные (или прямые, параллельные малой оси эллипса). Точки их пересечения (например, точка М) принадлежат эллипсу. Соединив полученные точки плавной кривой, получают эллипс (рисунок67, б).

а б

Рисунок 67

Парабола.Если круговой конус рассечь плоскостьюР, параллельной одной из его образующих, то в плоскости сечения получится парабола (рисунок 68).

Рисунок 68

Парабола (рисунок 69) – плоская кривая, каждая точка которой удалена на одинаковое расстояние от заданной прямойDD₁, называемойдиректрисой, и точкиF – фокуса параболы. Например, для точкиМ отрезкиMN (расстояние до директрисы) иMF (расстояние до фокуса) равны, т. е.MN =MF.

Парабола имеет форму разомкнутой кривой с одной осью симметрии, которая проходит через фокус параболы – точку F и расположена перпендикулярно к директрисе DD₁. Точна A, лежащая на середине отрезка OF, называется вершиной параболы. Расстояние от фокуса до директрисы – отрезок OF = 2OA – обозначают буквой р и называют параметром параболы. Чем больше параметр р, тем резче ветви параболы отходят от ее оси. Отрезок, заключенный между двумя точками параболы, расположенными симметрично относительно оси параболы, называется хордой (например, хорда MК).

Рисунок 69

Построение параболы по ее директрисе DD₁ и фокусу F(рисунок 70, а). Через точкуF перпендикулярно к директрисе проводят ось параболы до пересечения ее с директрисой в точкеО. ОтрезокOF =p делят пополам и получают точкуA – вершину параболы. На оси параболы от точкиA откладывают несколько постепенно увеличивающихся отрезков. Через точки деления1, 2, 3 и т. д. проводят прямые, параллельные директрисе. Приняв фокус параболы за центр, описывают дуги радиусомR₁ =L₁ до пересечения с прямой, проведенной через точку1, радиусомR₂ = L₂ до пересечения с прямой, проведенной через точку2, и т. д. Полученные точки принадлежат параболе. Вначале их соединяют тонкой плавной линией от руки, затем обводят по лекалу.

Построение параболы по ее оси, вершине А и промежуточной точке М (рисунок 70, б). Через вершинуA проводят прямую, перпендикулярную к оси параболы, а через точкуМ – прямую, параллельную оси. Обе прямые пересекаются в точкеB. ОтрезкиAB и BM делят на одинаковое число равных частей, а точки деления нумеруют в направлениях, указанных стрелками. Через вершинуA и точки1, 2, 3, 4 проводят лучи, а из точекI,II,III, IV– прямые, параллельные оси параболы. На пересечении прямых, обозначенных одинаковым номером, расположены точки, принадлежащие параболе. Обе ветви параболы одинаковы, поэтому другую ветвь строят симметрично первой с помощью хорд.

а б

Рисунок 70

Построение параболы, касательной к двум прямым OA и ОВ в данных на них точках A и В (рисунок 71, б). ОтрезкиOA иОВ делят на одинаковое число равных частей (например, на 8 частей). Полученные точки деления нумеруют и одноименные точки соединяют прямыми1–1, 2–2, 3–3 и т. д. Эти прямые являются касательными к параболической кривой. Далее в образованный прямыми контур вписывают плавную касательную кривую – параболу.

Рисунок 71

Гипербола.Если рассечь прямой и обратный конусы плоскостью, параллельной двум его образующим или в частном случае параллельной оси, то в плоскости сечения получится гипербола, состоящая из двух симметричных ветвей (рисунок 72, а).

Гиперболой (рисунок 72, б) называется незамкнутая плоская кривая, представляющая собой множество точек, разность расстояний которых от двух данных точек есть величина постоянная.

Рисунок 72

Постоянные точки F₁иF₂ называютсяфокусами, а расстояние между ними –фокусным расстоянием. Отрезки прямой (F₁MиF₂M), соединяющие какую-нибудь точку (M) кривой с фокусами, называютсярадиус–векторами гиперболы. Разность расстояний точки от фокусовF₁ иF₂ есть величина постоянная и равная расстоянию между вершинамиа и b гиперболы; например, для точкиM будем иметь:F₁M -F₂M = ab. Гипербола состоит из двух незамкнутых ветвей, имеет две взаимно перпендикулярные оси –действительную АВ имнимую CD. Прямыеpq иrs, проходящие через центрO, называютсяасимптотами.

Построение гиперболы по данным асимптотам pq иrs, фокусамF₁ иF₂ приведено на рисунке 72, б.

Действительная ось АВ гиперболы является биссектрисой угла, образованного асимптотами. Мнимая осьCDперпендикулярнаАВ и проходит через точкуО. Имея фокусыF₁ иF₂, определяют вершиныа иb гиперболы, для чего на отрезкеF₁F₂ строят полуокружность, которая пересекает асимптоты в точкахm ип. Из этих точек опускают перпендикуляры на осьABи на пересечении с ней получают вершиныа иb гиперболы.

Для построения правой ветви гиперболы на прямой АВ правее фокусаF₁ намечают произвольные точки1, 2, 3, ..., 5. ТочкиV иV1 гиперболы получаются, если принять отрезока5 за радиус и из точкиF2 провести дугу окружности, которую засекают из точкиF₁, радиусом, равнымb5. Остальные точки гиперболы строятся по аналогии с описанным.

Иногда приходится строить гиперболу, у которой асимптоты ОХ иOY взаимно перпендикулярны (рисунок 73). В этом случае действительная и мнимая оси будут биссектрисами прямых углов. Для построения задается одна из точек гиперболы, например точкаА.

Рисунок 73

Через точку A проводят прямыеАK иAM, параллельные осямох иoу. Из точкиOпересечения осей проводят прямые, пересекающие прямыеAM иАK в точках1, 2, 3, 4и1', 2', 3', 4'. Далее из точек пересечения с этими прямыми проводят вертикальные и горизонтальные отрезки до их взаимного пересечения в точкахI, II, III,IV и т. д. Полученные точки гиперболы соединяют с помощью лекала. Точки1, 2, 3, 4, расположенные на вертикальной прямой, берутся произвольно.

Эвольвента окружностиили развертка окружности.Эвольвентой окружностиназывается плоская кривая, которую описывает каждая точка прямой линии, если эту прямую катить без скольжения по неподвижной окружности (траектория точек окружности, образованная ее развертыванием и выпрямлением) (рисунок 74).

Для построения эвольвенты достаточно задать диаметр окружности D и начальное положение точки A (точку A₀). Через точку A₀ проводят касательную к окружности и на ней откладывают длину заданной окружности D. Полученный отрезок и окружность делят на одинаковое число частей и через точки деления окружности проводят в одном направлениикасательные к ней. На каждой касательной откладывают отрезки, взятые с горизонтальной прямой и соответственно равные1A₁ = A₀1,2A₂= В A₀2,3A₃= А₀3и т. д.; полученные точки соединяют по лекалу.

Рисунок 74

Спираль Архимеда- плоская кривая, которую описывает точкаA, равномерно вращающаяся вокруг неподвижной точки –полюсаОи одновременно равномерно удаляющаяся от него (рисунок 75). Расстояние, пройденное точкой при повороте прямой на 360°, называют шагом спирали. Точки, принадлежащие спирали Архимеда, строят исходя из определения кривой, задаваясь шагом и направлением вращения.

Построение спирали Архимеда по заданному шагу (отрезок ОА) и направлению вращения по часовой стрелке (рисунок 75). Через точку О проводят прямую, откладывают на ней величину шага спирали OA и, приняв его за радиус, описывают окружность. Окружность и отрезокOA делят на 12 равных частей. Через точки деления окружности проводят радиусыO1,O2,O3и т. д. и на них от точкиОоткладывают при помощи дуг соответственно 1/12, 2/12, 3/12 и т. д. радиуса окружности. Полученные точки соединяют по лекалу плавной кривой.

Спираль Архимеда является незамкнутой кривой, и при необходимости можно построить любое число ее витков. Для построения второго витка описывают окружность радиусом R = 2OAи повторяют все предыдущие построения.

Рисунок 75

Синусоида. Синусоидой называется проекция траектории точки, движущейся по цилиндрической винтовой линии, на плоскость, параллельную оси цилиндра. Движение точки складывается из равномерно–вращательного движения (вокруг оси цилиндра) и равномерно–поступательного (параллельно оси цилиндра). Синусоида – это плоская кривая, которая показывает изменение тригонометрической функции синуса в зависимости от изменения величины угла.

Для построения синусоиды (рисунок 76) через центр О окружности диаметра D проводят прямую ОХ и на ней откладывают отрезок O₁A, равный длине окружности D. Этот отрезок и окружность делят на одинаковое число равных частей. Из полученных и занумерованных точек проводят взаимно перпендикулярные прямые. Полученные точки пересечения этих прямых соединяют с помощью лекала плавной кривой.

Рисунок 76

Кардиоида.Кардиоидой (рисунок 77) называется замкнутая траектория точки окружности, которая катится без скольжения по неподвижной окружности таким же радиусом.

Рисунок 77

Из центра О проводят окружность заданного радиуса и берут на ней произвольную точкуM. Через эту точку проводят ряд секущих. На каждой секущей по обе стороны от точки пересечения ее с окружностью откладывают отрезки, равные диаметру окружностиM1. Так, секущаяIII3МIII₁ пересекает окружность в точке3; от этой точки откладывают отрезки3III и3III₁, равные диаметруM1. ТочкиIIIиIII₁, принадлежат кардиоиде. По аналогии,секущаяIV4MIV₁ пересекает окружность в точке4; от этой точки откладывают отрезкиIV4 и4IV₁, равные диаметруM1, получают точкиIV иIV₁ и т.д.

Найденные точки соединяют кривой, как указано на рисунке 77.

Циклоидальные кривые.Циклоиды – плоские кривые линии, описываемые точкой, принадлежащей окружности, катящейся без скольжения по прямой линии или окружности. Если при этом окружность катится по прямой линии, то точка описывает кривую, называемуюциклоидой.

Если окружность катится по другой окружности, находясь вне ее (по выпуклой части), то точка описывает кривую, называемуюэпициклоидой.

Если же окружность катится по другой окружности, находясь внутри ее (по вогнутой части), то точка описывает кривую, называемую гипоциклоидой. Окружность, на которой расположена точка, называетсяпроизводящей. Линия, по которой катится окружность, называетсянаправляющей.

Для построения циклоиды (рисунок 78) проводят окружность заданного радиусаR; на ней берут начальную точкуA и проводят направляющую прямуюАВ, по которой катится окружность.

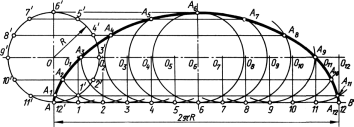
Рисунок 78

Делят заданную окружность на 12 равных частей (точки 1', 2', 3', ..., 12'). Если точка A переместится в положение A₁₂, то отрезок AA₁₂ будет равен длине заданной окружности, т. е. . Проводят линию центровО – O₁₂ производящей окружности, равную , и делят ее на 12 равных частей. Получают точки O₁, O₂, O₃, ..., O₁₂, являющиеся центрами производящей окружности. Из этих точек проводят окружности (или дуги окружностей) заданного радиуса R, которые касаются прямой АВ в точках 1, 2, 3, ..., 12. Если от каждой точки касания отложить на соответствующей окружности длину дуги, равную величине, на которую переместилась точка A, то получим точки, принадлежащие циклоиде. Например, для получения точки A₅ циклоиды следует из центра O₅ провести окружность и от точки касания 5 отложить по окружности дугу А5, равную А5', или из точки 5' провести прямую, параллельную АВ, до пересечения в точке A₅ с проведенной окружностью. Аналогично строят и все другие точки циклоиды.

Эпициклоида строится следующим образом. На рисунке 79 изображены производящая окружность радиусаR с центромO₀, начальная точкаA на ней и дуга направляющей окружности радиусаR₁, по которой катится окружность. Построение эпициклоиды аналогично построению циклоиды, а именно: делят заданную окружность на 12 равных частей (точки1', 2', 3', ..., 12'), каждую часть этой окружности откладывают от точкиA по дугеАВ 12 раз (точки1,2, 3, ..., 12) и получают длину дугиAA₁₂. Эту длину можно определить с помощью угла.

Далее из центра О радиусом, равнымOO₀, наносят линию центров производящей окружности и, проводя радиусы01, 02, 03, ...,012, продолженные до пересечения с линией центров, получают центрыО₁, О₂, ..., O₁₂производящей окружности. Из этих центров радиусом, равнымR, проводят окружности или дуги окружностей, на которых строят искомые точки кривой; Так, для получения точкиA₄следует провести дугу окружности радиусомO4' до пересечения с окружностью, проведенной из центраO₄. Аналогично строятся и другие точки, которые затем соединяются плавной кривой.

Рисунок 79

Построение гипоциклоиды аналогично описанному для эпициклоиды.