СОДЕРЖАНИЕ

1.1 Задача восстановления зависимостей по эмпирическим данным 4

1.2 Примеры задач, приводящих к проблеме переобучения при восстановлении зависимостей по эмпирическим данным 15

2 СУЩЕСТВУЮЩИЕ МЕТОДЫ ОТБОРА ПРИЗНАКОВОЙ ИНФОРМАЦИИ ПРИ ВОССТАНОВЛЕНИИ ЗАВИСИМОСТЕЙ ПО ЭМПИРИЧЕСКИМ ДАННЫМ 44

2.1 Гребневая регрессия 46

2.2Метод Lasso 49

2.3 Метод Elastic Net 52

2.4Метод Smoothly Clipped Absolute Deviation (SCAD) 58

2.5Адаптивный LASSO (АLASSO) 59

2.6Свойства регуляризованных оценок 61

3 МОДЕЛЬ ВОССТАНОВЛЕНИЯ ЗАВИСИМОCТЕЙ ПО ЭМПИРИЧЕСКИМ ДАННЫМ С РЕГУЛИРУЕМОЙ СЕЛЕКТИВНОСТЬЮ 65

3.1 Иерархическая вероятностная модель обучения восстановления зависимости с регулируемой селективностью. 65

3.2Общий алгоритм оптимизации критерия восстановления зависимости с регулируемой селективностью 70

3.3Свойства оценок параметров иерархической вероятностной модели с регулируемой селективностью 71

4СПИСОК ЛИТЕРАТУРЫ 78

5ПРЕЛОЖЕНИЕ 87

1 Проблема переобучения при восстановлении зависимостей по эипирическим данным и основные задачи исследования

1. Задача восстановления зависимостей по эмпирическим данным

Объектом исследований данной работы является выявление закономерностей и взаимосвязей в имеющихся множествах объектов или явлений реального мира между набором их явных характеристик, называемых признаками, с одной стороны и свойствами, скрытыми от непосредственного наблюдения, с другой. В литературе такая задача носит название задачи оценивания зависимостей по эмпирическим данным.

Задача оценивания зависимостей по эмпирическим данным является одной из наиболее трудных в современной информатике. Пусть - множество объектов произвольной природы, которые характеризуются некоторой зависимой (скрытой) переменной. Как правило, функция– известна нам только для некоторого ограниченного набора объектов, называемого обучающей совокупностьюгде- число наблюдений. Естественно, что компьютер не может непосредственно воспринимать физические объекты. Поэтому всегда необходима некоторая формальная переменная, выступающая как посредник между компьютером и природой, называемая признаком. Наиболее простым предположением является понимание признаковых представлений объектов как последовательностей действительных чисел, где- число признаков. В цели упрощения будем заменить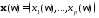обозначением

Требуется продлить функцию на все множество, чтобы иметь возможность оценивать значения зависимой переменной для других объектов . Предметом рассмотрения данной работы является случай, когда выходная переменная является действительнозначнойи исходная задача представляет собой задачу оценивания регрессионной зависимости. Еслипринимает значения из конечного множества, то такую задачу принято называть задачей обучения распознаванию образов. В нашей работе только будем рассматривать задачу оценивания регрессионной зависимости.

В данной работе мы будем придерживаться байесовского подхода к восстановлению зависимостей.

1. Проблема переобучения

Явление, которое часто встречается в ходе оценивания зависимостей по эмпирическим данным - переобучение. Переобучение - нежелательное явление, когда вероятность ошибки обученной модели на объектах контрольной совокупности оказывается существенно выше, чем средняя ошибка на обучающей совокупности. Такая модель обладает плохой обобщающей способностью. Целью оценивания зависимостей является создание модели с высокой обобщающей способностью. На практикепостроение модели выполняется только по объектам обучающей совокупности, но её эффективность оценивается на объектах контрольной совокупности. Строящий модель зависеть от обучающей совокупности, поэтому переобучение всегда происходит в задаче восстановления зависимостей по эмпирическим данным. С теоретической зрения, обработка переобучения имеет связь с понятием структирной минимизацой риска (Вапник и Червонекис, 1974).Но в данной диссертации, выберем более понятное изложение.

Одни из главных причин переобучения заключаются в малом размере обучающей совокупности, шуме обучающих данных и большом числе признаков (в сложной модели); например, в задаче микроматриц, где число признаков составляет тысяч или десятков тысяч генов. Очевидно, что во много практических задачах увеличение числа объектов обучающей совокупности невозможно, например, при исследовании опасной болезни, число исследованных пациентов обычно мало. В то же время определение шума обучающих данных очень трудно. Таким образом, чтобы избежать переобучения, необходимо уменьшить число признаков в модели (сложность модели).

Признаки делятся на релевантные и нерелевантные. Нерелевантные признаки не влияют на значение зависимой (скрытой) переменной, поэтому их нужно убирать. Очевидно, что если убираем слишком много признаков, то мы одновременно убираем и релевантные признаки, теряя информацию. Поэтому модель становится слишком простой и обладает плохим качеством. Данное нежелательное явление является недообучением. В этом случае получаются большие ошибки на и контрольной совокупности и обучающей совокупности. Если модель простая, смещение высокое и вариация малая. И наоборот, если модель сложная, смещение малое и вариация высокая. Нужно выбрать модель для компромисса между смещением и дисперсией, чтобы получить желательную модель, которая называется моделью пригонки(fitting).

По интуиции, можем иллюстрировать три явлений примером задачи восстановления полинома на рис.1.1. В слева рисунке, уровень полинома равен 1, модель слишком проста и имеет мало переменных, поэтому недообучение происходит. В справа рисунке, уровень полинома равен 9, модель слишком сложна и имеет много переменных, поэтому переобучение происходит. В остальном рисунке, уровень полинома равен 3, модель соотносится с явлением пригонка. Истинная зависимость показана сплошной линией, пунктирная линия соответствует восстановительным значениям.

Рисунок 1.1 Иллюстрирование явления: недообучение (слева), пригонка, и переобучение (справа). Истинная зависимость – сплошная линия, а восстановителный значение – нктирная линия.

Чтобы избежать явления переобучения, можно использовать несколько методов, например: скользящий контроль, регулирование и применение априорных распределений параметров. Методом регулирования является добавление информации, выражающейся штрафом, в модель. В машинном обучении известные примеры регулирования - гребневая регрессия, Lasso, Elastic Net,…Они рассматриваются тщательно в разделе 2. С точки байесовский зрения, методы регулирования соответствуют установлениею априорных распределений параметров модели.