Альфа-бета-процедура

В минимаксной процедуре процесс порождения дерева поиска и процесс оценки позиции полностью отделены друг от друга. Оценка позиции может начаться только лишь после порождения дерева поиска. Такое разделение иногда приводит к реализации крайне неэффективной стратегии. Показатель эффективности ветвления для этого алгоритма составляет 35 для шахмат и 361 для го. Если же оценивать концевые вершины и вычислять возвращенные значения по мере порождения дерева, то длительность поиска можно заметно сократить, порой даже на несколько порядков. К счастью, существуют более совершенные методы поиска, чем минимаксный. Все они так или иначе базируются на алгоритме альфа-бета отсечений.

Рассмотрим снова пример, приведенный на рисунке 2. Будем считать, что поиск ведется в глубину и что как только порождается концевая вершина, тут же вычисляется её статическая оценка.

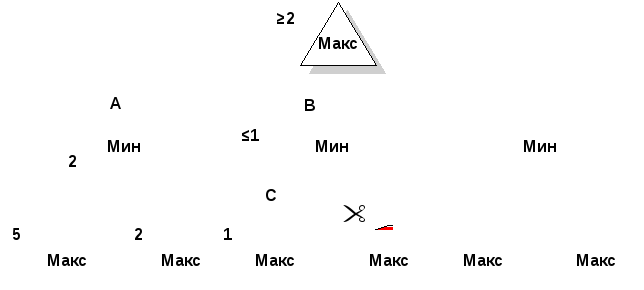
Рисунок 3. -отсечение

Будем считать, что возвращенное значение позиции вычисляется сразу же как только это становится возможным. Вершине А присваивается возвращенное значение (2). С этого момента становится ясно, что возвращенное значение исходной вершины ограничено снизу значением (2).

После того, как вершине С присваивается статическая оценка (1), возвращенное значение вершины В не может быть больше (1). Окончательное возвращенное значение вершины В, зависящее от статических оценок её потомков, может быть меньше, но не может быть больше.

Итак, возвращаемое значение исходной вершины ограничено снизу значением (2). Эту нижнюю границу будем называть значением для исходной вершины. Верхнюю границу вершины В, равную (1), будем называть значениемдля вершины В. Заметим, окончательное возвращенное значение вершины В не может превысить значениядля исходной вершины. Следовательно, дальнейший поиск на поддереве, ведущем из вершины В можно не проводить, т.к. вершина В заведомо не окажется более предпочтительной, чем вершина А.

Экономия при поиске была достигнута благодаря использованию тех границ, в которых заключены возвращаемые значения. В общем случае эти границы для данной вершины могут быть изменены после присвоения возвращенных значений её потомкам. Отметим, что:

• Значения для Макс вершин, в том числе и для исходной, не могут уменьшаться.

• Значения для Мин вершин не могут увеличиваться.

Благодаря этим ограничениям можно сформулировать следующие правила сокращения поиска:

• можно не проводить поиска на поддереве, растущим из всякой Мин вершины, -значение которой не превышает-значения всех её родительских Макс вершин. При этом окончательное возвращенное значение этой Мин вершины можно положить равным её-значению.

• можно не проводить поиска на поддереве, растущим из всякой Макс вершины, -значения которой не меньше-значений всех её родительских Мин вершин. При этом окончательное возвращенное значение для этой Макс вершины можно положить равным её-значению.

Если поиск прекращается в результате применения первого правила сокращения поиска, то говорят, что произошло -отсечение, а если в силу второго, то --отсечение. В процессе поиска значенияивычисляются по следующим правилам:

• для Макс вершины значение принимается равным наибольшему в данный момент значению среди окончательных возвращенных значений её дочерних вершин;

• для Мин вершины значение принимается равным наименьшему в данный момент значению среди окончательных возвращенных значений её дочерних вершин.

Весь процесс учета и-значений по мере прохождения дерева и произведения отсечения по первой возможности обычно называютальфа-бета -процедурой или методом граней и оценок.

Альфа-бета -процедура находит столь же хороший ход как и минимаксная процедура при поиске на ту же глубину, только гораздо быстрее.

Альфа-бета -процедура была разработана независимо друг от друга многими учеными в начале 60 годов XX века. Впервыепубликация с описанием альфа-бета отсечений появилась на русском языке в 1963 г в статье одного из разработчиков известной шахматной программы «КАИССА» А. Л. Брудно «Грани и оценки для сокращения перебора вариантов». На западе инициатором создания подобных процедур послужил Мак-Карти. Первой публикацией, в которой содержалось обсуждение отсечений в дереве игры, была статья Ньюэлла, Саймона и Шоу в 1958 г. с описанием их ранней шахматной программы, однако полное описание альфа-бета отсечений появилось в "западной" литературе по вычислениям и компьютерам в 1968 г. в статье Слейгла и Бурского о стратегиях доказательства теорем. Такие программы как DeepThoughtв шахматах (играющая на уровне гроссмейстера), чемпион мира по шашкам, программаChinookдостигли успеха во многом благодаря этому алгоритму.