Пример графа поиска для игры в 8.

Рисунок3.2

Оператор построения переемников очевидным образом зависит от соответствующих правил продукции. Систему управления с поиском на графе можно рассматривать как процесс выявления части неявно заданного графа, содержащей целевую вершину.

3. Общая процедура поиска на графе:

Алгоритм работы общей процедуры поиска на графе изображен на рисунке 3.3

Процедура порождает в явной форме граф G, называемый графом поиска, и подмножество Т данного графа, называемое деревом поиска. Дерево поиска определено указателями, которые устанавливаются на шаге 7. Каждая вершина из графаGимеет указатель, направленный только к одному из своих родителей. Этот указатель определяет также родителя данной вершины в дереве поиска Т

Граф поиска производит частичное упорядочение, поскольку ни одна вершина в графе Gне является собственным предком (шаг 6). Каждый возможный путь к какой – либо вершине, открытой этим алгоритмом, хранится в явном виде в графеGи только один выделенный путь определен к любой вершине дерева Т.

Схема алгоритма поиска на графе

Рисунок 3.3

Граф G

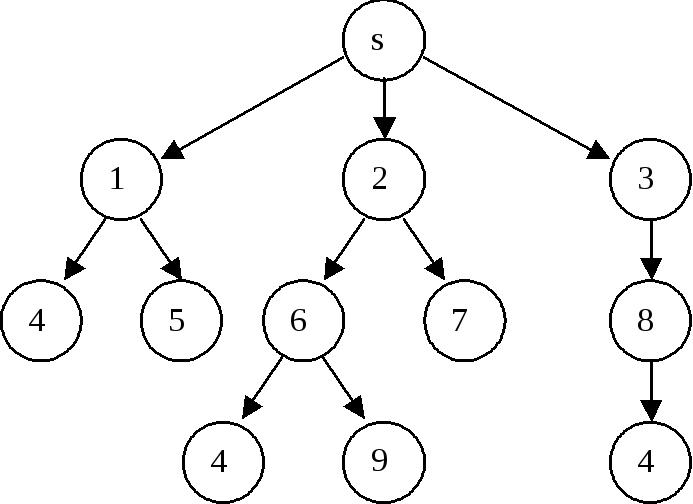
Рисунок 3.4

Дерево поиска т

Рисунок 3.5

Допустим, что в результате переупорядочения списка OPENна шаге 9 следующей вершиной для раскрытия была выбрана вершина 2, затем вершина 6, которая после раскрытия породила вершину 4. В дереве поискаTпоявился указатель от вершины 4 к вершине 6. Затем в ходе работы алгоритма была раскрыта вершина 1 и снова получена вершина 4. Если считать, что «стоимость» графа равна 1, то путь 4-1-sимеет меньшую «стоимость», чем путь 4-6-2-s, следовательно, указатель от вершины 4 в дереве поиска Т должен быть перенаправлен к вершине 1. Вершины в спискеOPENна каждом шаге работы алгоритма являются концевыми вершинами дерева поиска, а в спискеCLOSED- не концевыми. На шаге 3 процедуры вершины в спискеOPENявляются теми вершинами дерева поиска, которые еще не выбирались для раскрытия. Вершины в спискеCLOSEDявляются либо концевыми, которые уже выбирались для раскрытия, но не породили переемников, как, например, вершина 8, либо не концевыми вершинами дерева поиска. Процедура поиска на графе на шаге 9 упорядочивает вершины в спискеOPENтак, чтобы «лучшая» из них была выбрана для раскрытия на шаге 4. Это упорядочение может основываться как на произвольных критериях, так и на использовании эвристической информации о задаче. Каждый раз, когда выбранная для раскрытия вершина удовлетворяет терминальному условию, процесс поиска завершается. Путь от исходной вершины к целевой можно затем восстановить, прослеживая в обратном порядке указатели от целевой вершины к вершинеs. Процедура заканчивается неудачей, когда на дереве поиска не остается вершин, еще не выбранных для раскрытия. Если рассматриваемый граф поискаGне является деревом, то, возможно, что некоторая вершина из порожденных раскрытием вершиныnв спискеCLOSED. В этом случае имеется выбор между вычислительными затратами на проверку совпадения баз данных с одной стороны и затратами, связанными с порождением большего дерева поиска с другой.