1.3.3. Элементы математической статистики

Выборочное среднее , полученное по выборке объемом n:

. (1.3.7)

Выборочная дисперсия D, полученная по выборке объемом n:

. (1.3.8)

Выборочное среднее квадратическое отклонение

. (1.3.9)

Точность интервальной оценки по малой выборке

 = t,

где коэффициент Стьюдента t находится в соответствующих таблицах по числу степеней свободы f = n – 1 и доверительной вероятности Р_.

Поясним основные понятия на следующем примере. Рассмотрим значения случайной величины — скорости V (м/с) распространения механических волн в коже, измеренной у 20-летних молодых людей в области предплечья. Эта величина часто используется для оценки эффективности лечения и при диагностике.

Выборка – группа обследованных молодых людей; признак – значение скорости распространения механических волн.

Простой статистический ряд – последовательность значений случайной величины (скорости V), записанных в порядке получения. Такой ряд представлен в таблице 1:

Вариационный статистический ряд – таблица значений вариант, расположенных в упорядоченном виде с указанием их относительных частот. Такой ряд приведен в таблице 2:

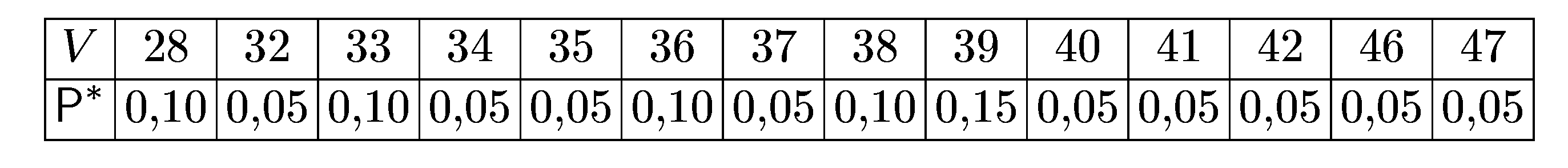
Полигон частот. Представим вариационный статистический ряд в графическом виде. Для этого на оси абсцисс отложим варианты, а на оси ординат – соответствующие им частоты. Нанеся точки вариационного ряда и соединив их ломаной линией, получим полигон частот (рис. 1).

Рис. 1. Полигон частот.

Интервальный статистический ряд – таблица интервалов с указанием частот. Для построения разобьем диапазон изменения скорости на равные интервалы. Число интервалов выбирается по усмотрению экспериментатора. Процесс разбиения можно проводить в следующем порядке.

а) Выберем число интервалов разбиения, например, 5.

б) Определим ширину интервала, разделив ширину диапазона на число интервалов:  = (47 – 28)/5 = 3,8.

в) Округлим полученное значение в большую сторону для того, чтобы суммарная ширина интервалов была несколько больше ширины диапазона (в нашем случае примем  = 4).

г) Двигаясь от левой границы диапазона вправо, найдем координаты точек, разбивающих диапазон на интервалы: х₁ = 28 + +  = 32, х² = 32 +  = 36, х³ = 36 +  = 40 и т. д.

д) Определим число точек, относимых к каждому из интервалов, и найдем соответствующие частоты (к интервалу (а, b) относят точки, удовлетворяющие неравенству (а  X < b): р₁^* =

= 2/20 = 0,1; р₂^* = 5/20 = 0,25 и т. д.

е) Сформируем интервальный статистический ряд:

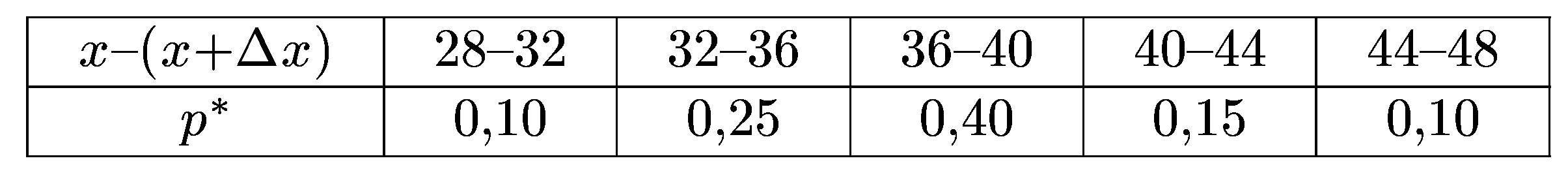
Гистограмма – графическое изображение интервального статистического ряда с учетом нормировки. Для построения на оси абсцисс отложим интервалы значений вариант и на каждом из них, как на основании, построим прямоугольник с высотой, равной его частоте, деленной на ширину интервала: h₁ = 0,1/4 =

= 0,025, h₂ = 0,25/4 = 0,0625 и т.д. При этом площадь каждого прямоугольника равна частоте попадания случайной величины в данный интервал, а сумма всех площадей равна 1 (рис. 2).

Рис. 2. Гистограмма

Найдем интервальную оценку генерального среднего Х_г для случайной величины, имеющей нормальное распределение (табл. 1). Объем выборки – 20. По формулам (1.3.7), (1.3.8), (1.3.9) найдем: = 37,05, = 5,02.

Зададим доверительную вероятность 0,95. По таблице коэффициентов Стьюдента найдем t = 2,08. Вычислим точность оценки:  = t= 2,095,0220 = 2,34 (м/с).

Получим интервальную оценку: Р (37,05 – 2,34 < Х_г < 37,05 + 2,34) = 0,95.