2.3.4. Связь вектора напряженности электрического поля и потенциала

Между вектором напряженности электрического поля и потенциалом существует следующая связь:

= – grad , (2.3.12)

где – дифференциальный оператор «набла», который является вектором. Действуя на любой скаляр, он превращает его в вектор:

grad  = ,

поэтому

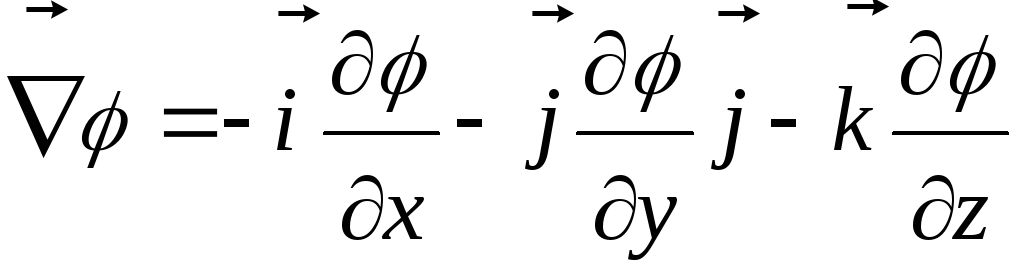= – . (2.3.13)

Как известно, любой вектор можно разложить на проекции по осям координат, то есть

(2.3.14)

Сравнивая формулы (2.3.13) и (2.3.14), получаем:

E_x = – (/x); E_y = – (/y); E_z = – (/z). (15)

Чтобы найти модуль вектора (его абсолютное значение), используют следующую формулу:

= E = (E²_x + E²_y + E²_z)^1/2. (2.3.16)

Между силой Кулона , действующей на электрический заряд со стороны электрического поля, и потенциальной энергией W этого заряда в данной точке поля существует связь, аналогичная связи между вектором напряженности и потенциалом:

= – grad W = – , (2.3.17)

_причем

F_x = – (W/x); F_y = – (W/y); F_z = – (W/z), (2.3.18)

а модуль силы Кулона

= F = (F²_x + F²_y + F²_z)^1/2. (2.3.19)

Пример 6. Потенциал электростатического поля зависит от координат по закону  = A. Найти величину напряженности электрического поля в точке Р(x₀,y₀,z₀), если А = 3 В, x₀ = y₀ = z₀ = 1 м, b = 1м.

Решение. Запишем исходные формулы (это формулы (2.3.13), (2.3.15), (2.3.16) соответственно):

= –;

E_x = – (/x); E_y = – (/y); E_z = – (/z);

 = E = (E²_x + E²_y + E²_z)^1/2.

Рассчитаем проекции вектора напряженности на оси координат по формуле (2.3.15):

E_x = – (/x) = – А(yz/b³); (2.3.20)

E_y = – (/y) = – A(xz/b³); (2.3.21)

E_z = – (/z) = – A(xy/b³). (2.3.22)

Подставляя в (2.3.20), (2.3.21) и (2.3.22) значения координат x = x₀, y = y₀, z = z₀ получаем:

E_x = – 3 В/м, E_y = – 3 В/м, E_z = – 3 В/м.

Результат подставляем в (2.3.16):

= E =(E²_x + E²_y + E²_z)^1/2 = 5,2 В/м.

Ответ: 5,2 В/м.

Пример 7. Потенциальная энергия точечного заряда в электростатическом поле зависит от координат по закону W = A. Найти величину силы Кулона, действующую на этот заряд в точке Р(x₀,y₀), если А = 2 Дж, x₀ = y₀ = z₀ = 1 м, b = 1м.

Решение. Запишем исходные формулы (это формулы (2.3.17), (2.3.18), (2.3.19) соответственно):

= – grad W = –,

F_x = – (W/x); F_y = – (W/y); F_z = – (W/z);

= F = (F²_x + F²_y + F²_z)^1/2.

Рассчитаем проекции вектора силы Кулона на оси координат по формуле (2.3.18):

F_x = – (W/x) = – А(yz²/b⁴); (2.3.23)

F_y = – (W/y) = – A(xz²/b⁴); (2.3.24)

F_z = – (W/z) = – 2A(xyz/b⁴). (2.3.25)

Подставляя в (2.3.23), (2.3.24) и (2.3.25) значения координат x = x₀, y = y₀, z = z₀, получаем:

F_x = – 2 Н, F_y = – 2 В/м, F_z = – 4 В/м.

Результат подставляем в (2.3.19):

 = F = (F²_x + F²_y + F²_z)^1/2 = 4,9 Н.

Ответ: 4,9 Н.

2.3.5. Диполь в электрическом поле

Электрический диполь – электронейтральная в целом система зарядов малого размера. Простейший диполь – это два точечных, одинаковых по величине и разных по знаку заряда, расстояние l между которыми мало по сравнению с расстоянием r от диполя то точки наблюдения.

Плечо простейшего диполя – это вектор , направленный от отрицательного заряда к положительному.

Электрический дипольный момент такого диполя вычисляется по формуле:

= q . (2.3.26)

В электрическом поле на диполь действует момент сил, модуль которого определяется выражением

М = р_еЕ_внsin, (2.3.27)

где  – угол между векторами и .

Пример 8.Диполь находится в электрическом поле, плечо диполя составляет 10^–10 м, его заряд 1,610^–19 Кл. Найти дипольный момент такого диполя.

Дано: l = 10^–10 м,

q = 1,610^–19 Кл.

Найти: р_е.

Решение. Дипольный момент диполя найдем с помощью формулы (2.3.26):

р_е = q l = 1,610^–29 Клм.

Ответ: 1,610^–29 Клм.

Пример 9. Диполь находится во внешнем электрическом поле напряженностью Е = 1000 В/м. Дипольный момент диполя составляет 410^–20 Клм. В начальный момент времени диполь ориентирован перпендикулярно линиям напряженности электрическогополя. Найти модуль момента сил, действующих на диполь в электрическом поле.

Дано: Е_вн = 1000 В/м,

р_е = 410^–20 Клм,

Найти: М.

Решение. Модуль момента сил, действующих на диполь в электрическом поле, найдем с помощью формулы (2.3.27):

М = р_еЕ_внsin.

По условию задачи  = 90, sin = 1, поэтому

М = р_еЕ_вн (2.3.28)

После подстановки числовых данных в (2.3.28), получим окончательный ответ:

М = p_eE_вн = 410^–17 Нм.

Ответ: 410^–17 Нм.