2.3. Тестовые задачи третьего уровня

2.3.1. Принцип суперпозиции для вектора напряженности электрического поля

Взаимодействие между зарядами осуществляется через поле. Всякий электрический заряд q изменяет определенным образом свойства окружающего его пространства – создает электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку другой, «пробный», заряд испытывает действие силы.

Силовой характеристикой электрического поля является напряженность – это сила, с которой электрическое поле действует на пробный заряд.

Величина напряженности поля неподвижного точечного заряда:

.(2.3.1)

Принцип суперпозиции для вектора напряженности электрического поля:

Напряженность системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:

. (2.3.2)

Электрическое поле принято изображать с помощью силовых линий – это линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности. Силовые линии электростатического поля не могут начинаться или заканчиваться в вакууме. Они начинаются на положительных и заканчиваются на отрицательных зарядах:

Пример 1. Имеются два точечных заряда q₁ = 2 нКл, q₂ = 1 нКл, находящиеся на одной прямой на расстоянии r = 50 см друг от друга (по условию задачи заряд q₁ расположен слева, заряд q₂ – справа). Найти модуль напряженности электростатического поля в точке О, расположенной между зарядами на расстоянии 10 см от заряда q₂.

Дано: q₁ = 2 нКл = 210^–9 Кл,

q₂ = 1 нКл = 110^–9 Кл,

r = 50 см = 0,5 м,

r₂ = 10 см = 0,1 м.

Найти: Е_рез.

Решение. Сделаем рисунок, на котором укажем расположение зарядов и точку О, в которой будем находить модуль результирующей напряженности. Выбираем направление оси x:

₂ q₁ q_{2 1}

А О В x

Здесь ₁ – напряженность, создаваемая в точке О зарядом q₁, ₂ – напряженность, создаваемая в точке О зарядом q₂. По условию задачи и в соответствии с рисунком, АВ = r = 0,5 м; ОВ = r₂ = 0,1 м; АО = r₁ = АВ – ОВ = r – r₂ = 0,5 – 0,1 = 0,4 м.

Запишем исходные формулы – формулу для расчета модуля напряженности поля точечного заряда (2.3.1) и принцип суперпозиции для вектора напряженности поля системы зарядов (2.3.2):

; .

Напряженность – это вектор. Чтобы найти модуль напряженности поля системы двух зарядов по формуле (2.3.2), необходимо рассчитать модули напряженностей Е₁ и Е₂, создаваемых зарядами q₁ и q₂ по формуле (1), а потом сложить их с учетом знака. Вектор ₂ противоположен выбранному нами направлению оси x, вектор ₁ направлен в ту же сторону, что и ось. Имеем:

Е_рез= Е₁ – Е₂. (2.3.3)

Теперь подставим числовые данные в формулу (2.3.1) и, используя формулу (2.3.3), получим окончательный ответ:

= 113 В/м; = 900 В/м;

Е_рез =Е₁ – Е₂ = 113 – 900 = 787 В/м.

Ответ: Е_рез = 787 В/м.

Пример 2. Имеются два точечных заряда q₁ = 2 нКл, q₂ = –1 нКл, находящиеся на одной прямой на расстоянии r = 50 см друг от друга (по условию задачи заряд q₁ расположен слева, заряд q₂ – справа). Найти модуль напряженности электростатического поля в точке О, расположенной между зарядами на расстоянии 10 см от заряда q₂.

Дано: q₁ = 2 нКл = 210^–9 Кл,

q₂ = – 1 нКл = – 110^–9 Кл,

r = 50 см = 0,5 м,

r₂ = 10 см = 0,1 м.

Найти: Е_рез.

Решение. Как и в примере 1, сделаем рисунок, на котором укажем расположение зарядов и точку О, в которой будем находить модуль результирующей напряженности.

q₁ q_{2 2 1}

А О В x

Здесь ₁ – напряженность, создаваемая в точке О зарядом q₁, ₂ – напряженность, создаваемая в точке О зарядом q₂ . Аналогично предыдущему примеру, АВ = r = 0,5 м; ОВ = r₂ = 0,1 м; АО = r₁ = 0,4 м.

Исходные формулы – формула для расчета модуля напряженности поля точечного заряда (2.3.1) и принцип суперпозиции для вектора напряженности поля системы из двух зарядов (2.3.2).

Как видно из рисунка, оба вектора ₂ и ₁ направлены в ту же сторону, что и ось x, поэтому формулу (2) можно записать как

Е_рез = Е₁ + Е₂. (2.3.4)

Теперь подставим числовые данные в формулу (2.3.1) и, используя формулу (2.3.4), получим окончательный ответ:

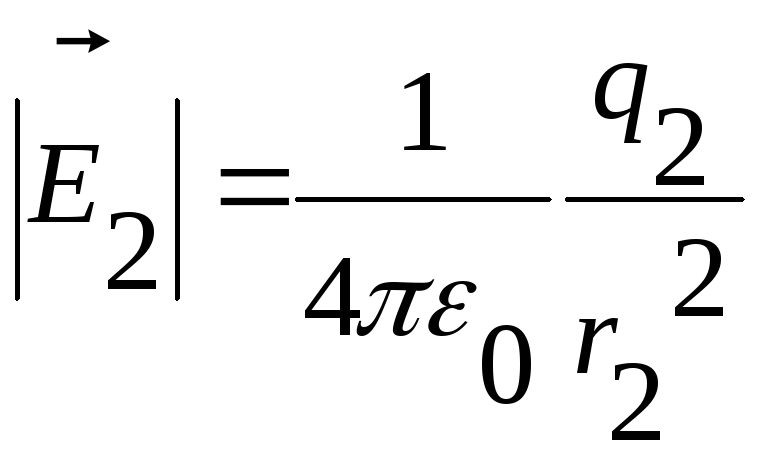= 113 В/м; = 900 В/м;

Е_рез = Е₁ + Е₂ = 1013 В/м.

Ответ: Е_рез = 1013 В/м.