1.3.8. Динамика вращательного движения твердого тела

Моментом импульса частицы, движущейся по некоторой траектории и имеющей в данный момент времени радиус вектор и импульс, относительно точки (центра)О, называется векторное произведение радиус-вектора и импульса частицы:

. (1.3.43)

Направление определяется правилом правого винта.

Векторное произведение любых векторов определяется следующим образом:

.

Закон изменения момента импульса:

. (1.3.44)

Здесь – момент силы.

* Скорость изменения момента импульса частицы относительно некоторой точки равна моменту силы относительно той же точки.

перпендикулярен векторам и, и образует с ними правую тройку векторов.

= rFsin, (1.3.45)

l = rsin,

где l – кратчайшее расстояние от точки О до линии действия силы – плечо силы.

Проекция вектора момента силы на некоторую фиксированную (закрепленную) ось, например ось z, называется моментом импульса относительно оси:

L_z = I, (1.3.46)

где I – момент инерции частицы,

I = mR². (1.3.47)

Закон изменения момента импульса относительно оси:

, (1.3.48)

где M_z – проекция момента силы на ось z.

Спроектируем уравнение моментов для системы материальных точек на ось вращенияOz , получим:

или .

Для абсолютно твердого тела I = const, поэтому

, (1.3.49)

то есть,

* произведение момента инерции на угловое ускорение равно результирующему моменту внешних сил относительно закрепленной оси вращения.

Уравнение (1.3.49) – основное уравнение вращательного движения твердого тела относительно закрепленной оси.

Здесь I играет роль меры инертности (как масса при поступательном движении).

Как следует из основного уравнения,

* Если моменты всех сил относительно оси уравновешены, то есть,  M_z = 0, то момент импульса тела (или системы тел) относительно той же оси сохраняется: L_z = I = const. Это частный случай закона сохранения момента импульса.

Момент инерции тела относительно оси равен сумме произведений масс его материальных точек на квадраты их расстояний до оси вращения:

I =  m_iR²_i.

Поскольку масса твердого тела распределена непрерывно, сумму следует заменить на интеграл. Тело разбивают на бесконечно малые объемы dV с массой dm = dV.

Таким образом,

I =  R² dm =  R²dV, (1.3.50)

где R – расстояние от элемента dV до оси вращения.

Пример 17. Вычислить момент инерции тонкого однородного стержня массы m и длины l относительно оси, проходящей через середину стержня, перпендикулярно ему.

l/2

dm

x

O C dx

ось

Решение. Ось, относительно которой нужно рассчитать момент инерции, проходит через центр масс стержня (точку С), так как по условию задачи он однороден. Выделим элемент массы dm стержня и длины dx. Момент инерции стержня относительно оси, проходящей через его центр масс, найдем из выражения (1.3.50), учитывая, что dV = dx, так как по условию задачи стержень тонкий, а масса единицы объема (в нашем случае масса единицы длины) определяется выражением  = m/l:

.

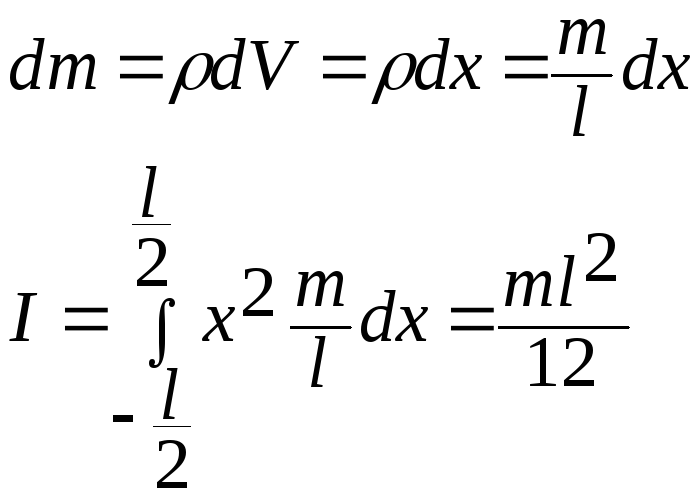Пример 18. Рассчитать момент инерции стержня (см. пример 17) относительно оси, проходящей через один из его концов (точку О).

Решение. Согласно (1.3.50),

.

Моменты инерции тел относительно оси, проходящей через центр масс:

Тонкого обруча: I_C = mR²; (1.3.51)

Диска (цилиндра): I_C = (1/2) mR²; (1.3.52)

Шара: I_C = (2/5) mR². (1.3.53)

Если момент инерции I_C относительно оси, проходящей через центр масс, известен, то можно легко вычислить момент инерции относительно любой параллельной ей оси О, проходящей на расстоянии d от центра масс по теореме Штейнера:

* Момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной ей и проходящей через центр масс, и произведения массы тела на квадрат расстояния между осями:

I₀ = I_C + md². (1.3.54)

Пример 19. Рассчитать момент инерции тонкого однородного стержня массы m и длины l относительно оси, проходящей через его конец (точку О), используя теорему Штейнера.

Решение. Момент инерции стержня относительно центра масс, согласно примеру 17, равно I_C = ml²/12. Расстояние между осями d составляет d =l/2. По теореме Штейнера (1.3.54) имеем:

I₀ = I_C + m(l/2)² = ml²/12 + ml²/4 = ml²/3.

Пример 20. Тонкий однородный стержень массы 1 кг и длиной 1 м вращается в вертикальной плоскости без трения вокруг горизонтальной оси, проходящей через его конец. Стержень располагают под углом 30 к горизонту и отпускают без толчка. Найти угловое ускорение стержня в начальный момент времени. Ускорение свободного паления считать равным 10 м/с².

Дано: m = 1 кг;

l = 1 м;

 = 30;

g = 10 м/с².

Найти: .

Решение.

А В



r C

Введем следующие обозначения: АС = l, АВ = ВС = l/2, плечо силы тяжести (она действует на центр масс однородного стержня, находящегося в точке В, посередине стержня) r = (l/2)cos. Тогда, используя основное уравнение динамики вращательного движения (1.3.49), запишем:

M = I,

откуда

 = M/I. (1.3.55)

Найдем момент силы тяжести М из (8.3):

М = mg = (mglcos)/2. (1.3.56)

Момент инерции стержня относительно оси, проходящей через один из его концов, мы рассчитали в примере 18: , поэтому, подставляя полученные выражения для момента инерции и момента сил (1.3.56) в (1.3.55), получим окончательно:

 = M/I = (3mglcos)/(2ml²) = (3gcos)/(2l) = 13 (рад/с²).

Ответ: 13 рад/с².

Пример 21. Некоторое тело вращается вокруг закрепленной оси без трения. Его момент импульса относительно этой оси зависит от времени по закону L(t) = At² + Bt + C. Через 0,5 секунд после начала вращения тело имело угловое ускорение 2 рад/с². Найти зависимость момента инерции тела от времени и его величину через 0,5 секунд после начала вращения. А = 1 кгм²/с³, В = 2 кгм²/с², С = 1 кгм²/с.

Дано: L(t) = At² + Bt + C;

t = 0,5 с;

 = 2 рад/с²;

А = 1 кгм²/с³, В = 2 кгм²/с², С = 1 кгм²/с.

Найти: I(t), I.

Решение. Запишем основное уравнение динамики вращательного движения (1.3.49), откуда выразим момент инерции:

.

Чтобы рассчитать момент инерции тела в момент времени 0,5 с, подставим в полученное выражение значения углового ускорения и коэффициентов А и В:

I = (1/2)(210,5 + 2) = 1,5 (кгм²).

Ответ: I(t) = 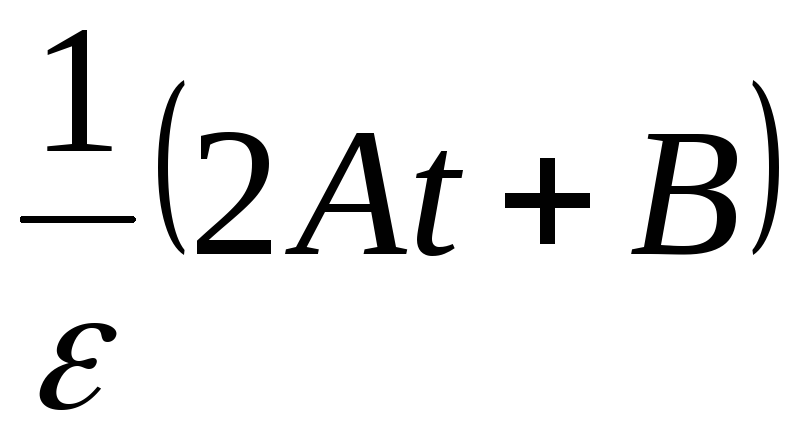; I = 1,5 кгм².