3.2.3. Сравнение дисперсий и средних

Одной из важнейших задач статистической обработки наблюдений является сравнение двух или более средних и дисперсий. Основной решаемый при этом вопрос – можно ли считать сравниваемые выборочные величины оценками одной и той же генеральной совокупности.

Сравним две дисперсии и, имеющие соответственноистепеней свободы, сделанные из генеральной совокупности с дисперсиейи генеральной совокупности с дисперсией.

В качестве критерия значимости в этом случае используется так называемое распределение Фишера (F - распределение). Это распределение случайной величины

(7)

зависящей только от числа степеней свободы, при этом. Квантили F – распределения приведены в таблицах.

При сравнении несколько дисперсий ,,…,, имеющих степени свободы используется критерий Бартлета.

При сравнении средних мы должны убедиться, что истинное среднее значение измеряемой величины остается неизменным.

Пусть заданы две случайные выборки:

взятые из нормально распределенных генеральных совокупностей, генеральные средние и генеральные дисперсии которых равны: и . Тогда среднее значение первой выборки есть нормально распределенная случайная величина с параметрами и , а среднее второй выборки с параметрами и. Нулевая гипотеза о равенстве отвергается, если при двустороннем критерии выполняется неравенство

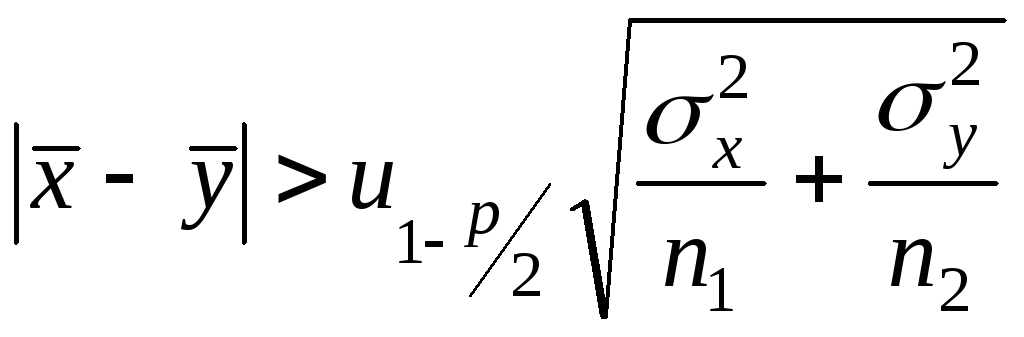(8)

Данный критерий прост и надежен, но он требует значения и, что не всегда возможно. Если генеральные дисперсии неизвестны, то используют выборочные дисперсиииираспределение Стьюдента. При этом генеральная дисперсия оценивается средневзвешенной

С использованием критерия Стьюдента при числе степеней свободы нулевая гипотеза отвергается, если при двустороннем критерии:

(9)

3.2.4. Дисперсионный анализ

В процессе проведения экспериментальных исследований зачастую возникает ситуация, когда один или несколько основных факторов начинают заданным образом изменяться. Эти изменения могут повлиять на результаты наблюдений, и степень этого влияния может быть исследована методами математической статистики.

Влияние изучаемых факторов может быть двояким: они могут изменять как истинный результат (среднее значение), так и дисперсию этих наблюдений. В большинстве случаев при использовании одной и той же методики и приборов при проведении экспериментов дисперсия наблюдений остается неизменной. Однако отсутствие влияния изменяющихся факторов на дисперсию наблюдений должно быть доказано.

Такой подход, заключающийся в исследовании влияния переменных факторов, на изменение дисперсий называется дисперсионным анализом.

Рассмотрим схему дисперсионного анализа, когда генеральная дисперсия заранее неизвестна.

При исследовании влияния фактора А на уровнях надо обязательно иметь дублирующие наблюдения на некоторых его уровнях. Если на всех уровнях А_i проводится одинаковое число наблюдений, то будем иметь статистики

где n – число наблюдений на каждом уровне.

Средние значения определяются:

а среднее всех наблюдений по всем уровням

общая выборочная дисперсия всех наблюдений

.

Основной задачей дисперсионного анализа является разложение общей дисперсии на составляющие, характеризующие факторА и фактор случайности в отдельности. Фактор случайности можно оценить, благодаря наличию повторных наблюдений на каждом уровне

то есть получить серию выборочных дисперсий . По этим значениям можно найти оценку генеральной дисперсии

,

имеющую k(n-1) степеней свободы.

О влиянии фактора А можно судить по остаточной дисперсии

.

Эта оценка слишком груба и более точной является

.

Для того, чтобы влияние фактора А было значительным, необходимо и достаточно, чтобы дисперсия существенно отличалась от, что можно проверить покритерию Фишера

(10)

где F_1-p – распределение Фишера с f₁ = k – 1 и f₂ = k (n - 1) степенями свободы.