
XXX
.pdfМинистерство образования и науки Российской Федерации Государственное образовательное учреждение
высшего профессионального образования Тульский государственный университет
Контрольно-курсовая работа
по курсу общей физики Часть 2
Вариант №16
Выполнил студент гр. 130101 Орлов Ю.И.
Проверил доцент |
Жигунов К.В. |
Тула 2011

Контрольно-курсовая работа по курсу общей физики. Часть 2 |
2 |
1.Задание 12.2
Два прямолинейных бесконечно длинных провод- |
|
|
|
|
ника расположены перпендикулярно друг к другу. |
|
|
|
|
|
|
|
|
|
Найти индукцию магнитного поля в точке М. |
|
|
|
|
I1 = 3:16A, I2 = 2:4A, AB = 3 см, d = 5 см. |
M |
d |
|
|
Решение: |
|
|
|
|
|
|
A |
B |
|
Модуль магнитной индукции на расстоянии r |
|
|
|
|
от бесконечно длинного проводника с током можно |
|
|
|
|
найти по формуле: |
|
|
|
|
|
|
|
|
|
B= 0I 2 r
Направление вектора магнитной индукции направляется по направлению
~
векторного произведения [dl; ~r]. Т.к. проводники с токами расположены взаимноперпендикулярно, то и векторы магнитных индукций, создаваемых каждым проводником, расположены перпендикулярно и модуль суммы их
p
векторов можно найти как B = B12 + B22. Тогда:
B = qB12 + B22 = 2 r |
( d )2 |
+ (d + AB )2 |
= 14 мкТл |
|||||
|
|
|
0 |
|
I1 |
|
I2 |
|
Ответ: 14 мкТл.
Орлов Ю. И. |
гр. 130101 |
3 |
2. Задание 12.6 |
|
|
|
|
|
|
|
|
||
Линейный проводник, по которому проходит ток |
|
|||||||||
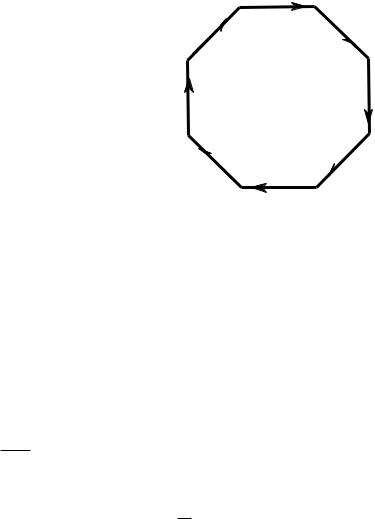
I, образует жесткий контур в форме правильно- |
I |
|||||||||
го многоугольника со стороной l. Найти индукцию |
||||||||||
|
||||||||||
магнитного поля в центре контура. |
|
|||||||||
l = 14 см, I = 2.5 А. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
Решение: |
|
|
|
|
|
|
|
|
||
Данный контур можно разбить на 8 линейных |
|
|
|
|||||||
|
|
|||||||||
частей и рассмотреть одну из них. Результирую- |
|
|||||||||
щий модуль вектора магнитной индукции будет в |
|
|||||||||
8 раз больше, чем для рассчитанного одного. |
|
|||||||||
Найдём расстояние от проводника до центра |
|
|||||||||
фигуры. По свойствам правильного многоугольника: |
|
|||||||||
|
|
l = 2r tg |
|
|
|
|||||
|
|
|
|
|||||||
|
|
8 |
|
|
|
|
||||
r = |
l |
ctg |
|
= 1021:3 см |
|
|||||
|
|
|
||||||||
2 |
8 |
|
|
|
|
|
|
|||
Модуль индукции магнитного поля, создаваемого отрезком с током, можно определить по формуле:
B = 4r0I (cos 1 cos 2)
Отрезок с центром описывает равнобедренный треугольник с углом при вершине, т.к. фигура правильный восьмиугольник, 28 = 4 , отсюда угол при
основании: 1 = ( 4 )=2 = |
3 |
, тогда 2 |
= |
3 |
= |
5 |
. Подставив эти |
||||||||
8 |
8 |
8 |
|||||||||||||
значения, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
B = |
02:5 |
(cos |
3 |
|
5 |
) = 18; 75нТл |
||||||||
|
8 |
4 1021:3 10 2 |
8 |
|
8 |
||||||||||
B = 150нТл
Ответ: 150 нТл.
Контрольно-курсовая работа по курсу общей физики. Часть 2 |
4 |
3.Задание 12.7
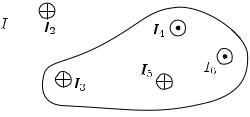
Найти циркуляцию вектора индукции магнитного поля, образованного системой линейных проводников с током, по конту- 
 ру, указанным на рисунке.
ру, указанным на рисунке.
I1 = 1:6 A, I2 = 2:7 A, I3 = 1:1 A, I4 = 1:4 A, I5 = 0:6 A, I6 = 1:9 A.
Решение: |
PI. Тогда: |
|
Известно, что R Bdl~ ~ = 0 |
||
Z |
Bdl~ ~ = 0(I4 + I6 I3 I5) = 0(I4 + I6 I3 |
|
 l
l
I5) = 2 10 6 Тл м
Ответ: 2 10 6 Тл м

Орлов Ю. И. |
гр. 130101 |
5 |
4.Задание 13.2
Заряженная частица, ускоренная разностью потенциалов U, влетает в однородное магнитное поле под углом к направлению поля и начинает двигаться по винтовой линии. Индукция магнитного поля - B, радиус витка винтовой линии - R, шаг винтовой линии - h. Найти неизвестные величины.
Частица: протон; U =?; = 60 ; B = 0:346 Тл; R = 2 см; h =? Решение: Рассмотрим движение частицы в магнитном поле. Вектор ско-
рости ~v можно разложить на две составляющие: ~vn - скорость направленная вдоль линий индукции и ~v - перпендикулярна линиям индукции. Тогда найдём эти скорости так:
vn = v cos ; v = v sin ;
При движении частицы с направлении ~v , её траектория будет закручиваться. Найдём радиус получаемой окружности. Найдём ускорение, действующее на частицу:
|
|
a = |
v B |
|
||||
Тогда радиус окружности |
|
m |
||||||
|
|
|
||||||
|
|
|
|
|
|
|
||
R = |
v2 |
= |
mv |
|
= |
|
mv sin |
|
a |
B |
|
|
B |
||||
|
|
|
|
|
||||
Найдём шаг винтовой траектории. Для этого найдём период обращения частицы:
T= 2 = 2 R = 2 m
!v B
Тогда найдём шаг винтовой траектории:
h = vn T = 2 mvn = 2 mv cos
B B
Рассмотрим движение частицы в электростатическом поле. По закону сохранения энергии:
2 |
+ q = const; qU = const; v = r |
2m |
|
mv2 |
|
|
qU |
Учитывая эти формулы, рассчитаем недостающие значения:
|
h = |
2 mv cos |
|
= 2 R ctg = 7:26 см |
||||
|
|
|||||||
|
|
|
|
B |
|
|
|
|
|
mv2 |
|
|
(BR)2 |
|
(BR)2 |
||
U = |
|
= |
|
= |
|
= 1:91 1022 В |
||
2q |
2qm sin2 |
2qm sin2 |
||||||
Ответ: h = 7.26 см; U = 1:91 1022 В.

Контрольно-курсовая работа по курсу общей физики. Часть 2 |
6 |
5.Задание 13.2
Через сечение S = ab металлической пластинки (а - толщина, b - высота) пропускают ток I. Пластинка помещена в магнитное поле с индукцией B, перпендикулярное ребру b и направлению тока. При этом возникает поперечная разность потенциалов U. Найти неизвестную величину. Концентрацию электронов проводимости считать равной концентрации атомов.
Металл: алюминий; I = 6 А; B = 0.26 Тл; U = 3:6 10 7; a =? Решение: Рассмотрим движение электрона в проводнике. Под действи-
ем магнитного поля, на электрон действует сила, равная FB = evB. В результате смещения электрона, возникает электрическое поле, действующая на частицу против силы Лоренца и равная FE = eE. В конечном итоге, установится равновесие, когда данные силы будут равны по модулю. Тогда: eE = evB; E = vB v - средняя скорость электрона, найдём из выражения:
j = nev; v = nej
j - плотность тока, найдём так:
j = SI = abI
Тогда подставив получим:
E = neabI B
Найдём концентрацию носителей заряда:
n = |
N |
= |
N |
= |
NA |
= |
6; 022 1023 |
= 6; 022 |
|
1016 |
|
|
|
|
|
10 106 |
|||||||
|
V |
|
|
V |
|
VM |
|
|
|||
Поперечную разность потенциалов найдём как:
U = Eb = neaIB
Отсюда найдём a:
a = |
IB |
= |
|
6 0:26 |
= 4:5 |
|
108 |
м |
|
|
10 7 6; 022 1016 1:602 10 19 |
||||||
|
Une 3:6 |
|
|
|||||
Ответ: 4:5 108 м

Орлов Ю. И. |
гр. 130101 |
7 |
6.Задание 13.6
Между полюсами электромагнит создаётся однородное магнитное поле, индукция которого равна B. По проводу длинной l, расположенному между полюсами электромагнита под углом к силовым линиям, за время t проходит количество электричества, определяемое законом q = f(t). Сила, действующая при этом на провод равна F. Найти неизвестную величину.
q = 0.4 t - 0.17; l = 11 см; B = 0.0096 Тл; = 60 ; F = ? Решение: Согласно закону Ампера:
~ |
~ ~ |
dF |
= [Idl; B] |
или
dF = IdlB sin
Проинтегрировав, получим:
Z l
F = IB sin dl = IlB sin
0
Ток найдём как
I = dqdt = 0:4
Тогда
F = 0; 4 0; 11 0; 0096 sin 60 = 365:8 мкН
Ответ: 365.8 мкН
Контрольно-курсовая работа по курсу общей физики. Часть 2 |
8 |
7.Задание 13.7
Из проволоки l изготовлены контуры различного вида. Вращающий момент сил, действующий на каждый контур, помещённый в однородное магнитное поле с индукцией B, равен M. По контуру проходит ток I. Нормаль к плоскости контура составляет угол с направлением магнитного поля. Найти неизвестную величину.
Вид контура: круговой; l = 31.4 см; B = 0.007 Тл; M = ?; I = 0.4 А;
= 30
Решение:
Момент, приобретаемый рамкой, можно рассчитать по формуле:
M = ISB sin
Площадь рамки S расчитаем так:
|
|
|
S = r2 |
|||||||
|
|
|
l = 2 r |
|||||||
|
|
S = ( |
l |
|
)2 |
= |
l2 |
|
||
|
|
|
|
|
4 |
|||||
|
|
|
2 |
|
||||||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
l2 |
0:3142 |
|
0:007 sin 30 = 1:1 10 5 Н м |
||||||
M = I |
|
B sin = 0:4 |
|
|
||||||
4 |
4 |
|||||||||
Ответ: M = 1:1 10 5 Н м
