Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

решение 18 вариант

.pdf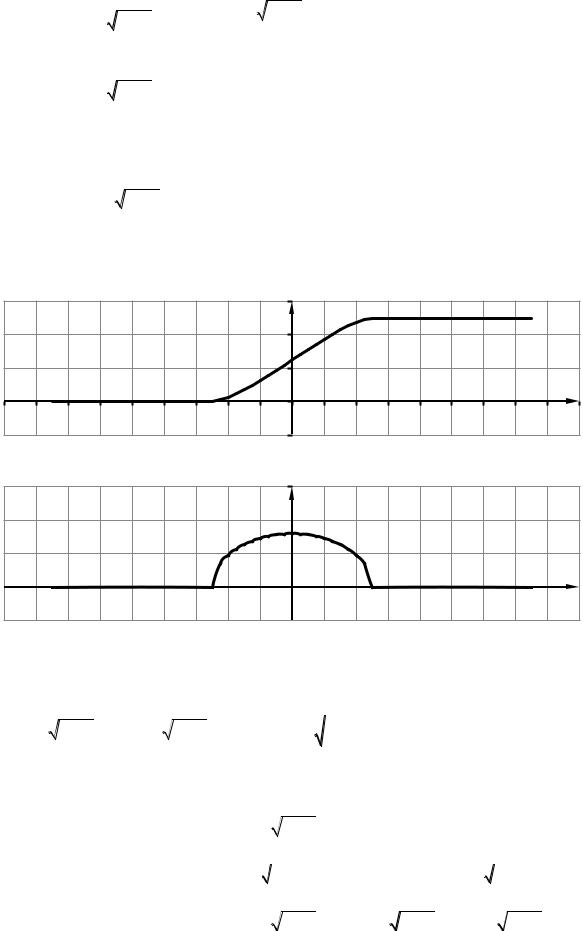

Скачиваний:

192

Добавлен:

10.05.2015

Размер:

720.15 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

1
1	2	x					dx arcsin x x	1 x		2		1
F(x) 0dx	2				1 x2			1 x				1
F(x) 0dx					1 x2
		1										2
		1
Если x>1, то f(x)=0, следовательно,
1		1					x
F(x) 0dx	2					dx 0dx arcsin1			1
	2			1 x2					1		1
				1 x2							1
		1	1						2

Интегральная функция распределения равна

0,	x 1,

		1 x2
arcsin x x		1 x2	1	,	1 x 1
F(x) =			2	,	1 x 1
			2
1,	x 1

Построим график F(X)
					1,2
					0,8
					0,4
					0
-3,6 -3,2 -2,8 -2,4	-2	-1,6	-1,2	-0,8	-0,4	0	0,4	0,8	1,2	1,6	2	2,4	2,8	3,2	3,6
					-0,4
Построим график f(X):

1,2

											0,8
											0,8
											0,4
											0,4
												0
-3,6		-3,2 -2,8 -2,4 -2				-1,6 -1,2 -0,8					-0,4			0					0,4		0,8			1,2 1,6			2	2,4			2,8 3,2	3,6
											-0,4
											-0,4

Находим математическое ожидание по формуле																							M X xf (x)dx

В нашем случае имеем,
		1				1																			1

	2				1				d 1 x2							2				1 x2			3
		x		dx
M			1 x2					1 x2																		0
M			1 x2					1 x2									3									0
		1				1											3								1
		1				1																			1
Дисперсию находим по формуле D X
Дисперсию находим по формуле D X															x2 f (x)dx (M (X ))2

								D X		2	1
										2	x2			1 x2 dx
											x2			1 x2 dx
											1
											1
							u x, dv x											dx;			тогда du dx,v 1
В нашем случае имеем,							u x, dv x						1 x2					dx;			тогда du dx,v 1									1 x2
																												3
								D X		2	1												2				1	2	1			1
											1																1		1
											x2			1 x2 dx											x 1 x2						1 x2 dx
											x2			1 x2 dx								3			x 1 x2			3			1 x2 dx	3
											1											3					1	3		1		3
											1																1			1

Среднеквадратическое отклонение равно X D(X) 0,333 0,577

Находим вероятность попадания CВ Х в интервал (0; 0,5).

0,5		2	0,5
P(0 X 0,5)	f (x)dx	2		1 x2 dx 0,305
P(0 X 0,5)	f (x)dx			1 x2 dx 0,305
0			0

Задание 7б. Непрерывная случайная величина Х имеет функцию

распределения F(x). Требуется:

1)найти коэффициент а;

2)найти плотность распределения f(x);

3)построить графики f(x) и F(x);

4)найти вероятность попадания случайной величины Х в интервал (х1, х2).

Решение. 1) При х = π функция F(x ) равна 1, т.е. a ∙ cos (2π) =1.

Откуда a =1.

2) Найдем плотность распределения вероятностей:

	0, x 3
		4
		4
			3
			3
f (X ) F (x) 2sin 2x,				x
f (X ) F (x) 2sin 2x,			4	x
		x	4
	0,	x



Проверим, что		f (x)dx 1

						3
	f (x)dx 2sin 2xdx cos 2x					3	1
	f (x)dx 2sin 2xdx cos 2x				3 cos 2 cos	2	1
		3			4	2
		3
		4

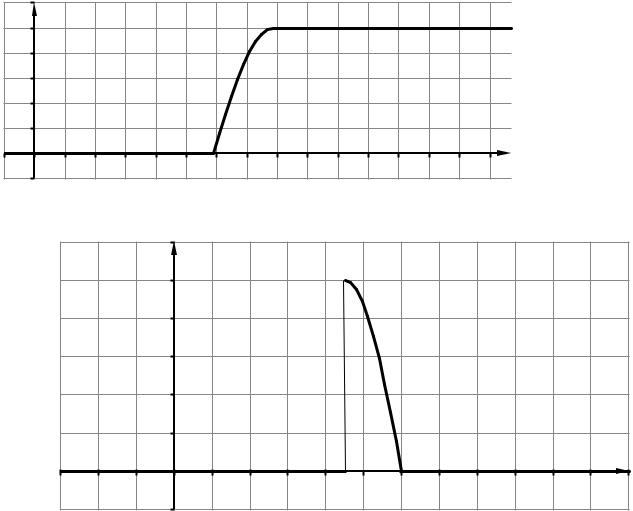
3)	Построим график F(X)
1,2
1
0,8
0,6
0,4
0,2
0
-0,4	0	0,4	0,8	1,2	1,6	2	2,4	2,8	3,2	3,6	4	4,4	4,8	5,2	5,6	6
-0,2
Построим график f(X):

2,4
2
1,6
1,2
0,8
0,4
0
-1,57 -1,047 -0,524 -0,001 0,522 1,045	1,568	2,091	2,614	3,137	3,66	4,183	4,706	5,229	5,752	6,275
-0,4

4)найдем вероятность попадания случайной величины Х в интервал (0, /3).

P(0 X				F 0 0 0	0
P(0 X		) F		F 0 0 0	0
	3		3

Задание 8.

Случайная величина ХN( ; ) (распределена по нормальному закону).

Найти вероятность того, что эта случайная величина примет значение:

1)в интервале [a; b]; 2)меньше K; 3) больше L; 4) отличающееся от среднего значения по абсолютной величине не более чем на .

Значения параметров , , а, b, K, L и вычисляются по следующим формулам:

=N - номер варианта; = остаток ( N/8) + 2; = остаток ( N/5) + 1; a =

N - ; b = N+2 ; K =N - ; L = N+ 2 .

Решение. =18; = 4; = 4; a = 14; b = 26 ; K =14; L = 26; ХN(18;4)

1)Вероятность того, что X примет значение, принадлежащее интервалу (a, b),

b			a
P(a X b)

где Ф(х) – функция Лапласа

Отсюда, вероятность того, что X примет значение, принадлежащее интервалу (14, 26), с учетом нечетности функции Лапласа, равна

	26 18	14 18		2 1 2 1
P(14 X 26)			4	2 1 2 1
	4		4

0, 4772 0,3413 0,8185

2) вероятность	того,	что X примет значение	меньше K=14
P(X 14)	14 18	1 ( 0,5)
P(X 14)		1 ( 0,5)
	4

0,5 0,3413 0,1587

3)вероятность того, что эта случайная величина примет значение больше L=26

	26 18	0,5 0, 4772 0,0228
P(X 26) 0,5		0,5 0, 4772 0,0228
	4

4) вероятность того, что эта случайная величина примет значение

отличающееся от среднего значения по абсолютной величине не

более чем на =4

Воспользуемся формулой

P( X ) 2

Имеем

P(	X 18		4	2 (1)	2 0,3413 0,6826
			4
		4) 2
			4

Ответ: 1) 0,8185; 2)0,1587 ; 3) 0,0228; 4)0,6826 .

Задание 9.

Плотность распределения вероятностей случайной величины Х имеет

вид f (x) Aeax2 bx c . Найти значение параметра А, М(Х), D(X), функцию

распределения F(X), вероятность P(х1 X х2). Исходные данные приведены в таблице:

№ вар	а	b	с	х1	x2

18	-3	-4	0	1/3	4/3

Решение. Плотность распределения обладает следующим свойством:

f (x)dx 1

Отсюда, учитывая, что интеграл Пуассона e u2 du , имеем:


			4				4			2	2
			A e3			4	A e3							2

	2				3x2 4x				3x


1	Ae 3x	4xdx		Ae		3 d 3x		e		3		d	3x
1	Ae 3x	4xdx		Ae		3 d 3x		e				d	3x
			3				3							3

A e3 ; 3

	4	3
A e	3
A e	3

Математическое ожидание непрерывной случайной величины X, возможные

значения которой принадлежат всей оси Ох, определяется равенством

			4
			4		3
M(X ) xf (x)dx e 3					3	xe 3x2 4xdx
M(X ) xf (x)dx e 3						xe 3x2 4xdx


Находим интеграл xe 3x2 4xdx по частям
							4
u x, dv e 3x2 4xdx du dx,v e 3x2 4xdx								e	3	e u2 du


							3
		4
	2e3			; M X			2
xe 3x2 4xdx	2e3						2
							3
	3	3
	3	3

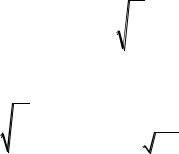
Дисперсию D(X) находим по формуле

				4
				4	3					4	11	4	1
D(X ) x2 f (x)dx M(X ) 2 e				3	3		x2e 3x2 4xdx			4		4	1
D(X ) x2 f (x)dx M(X ) 2 e				3			x2e 3x2 4xdx
										9	18	9	6

Находим функцию распределения F(X), воспользуемся формулой
x	4		x						x
x	4	3	x			1			x
F(x) f (x)dx e	3	3	e 3x2 4xdx			1			e u2 /2du (x)
	3
								2
								2

Функция Лапласа имеет известные таблицы значений Вероятность P(1/3 < X < 4/3) находим по таблице

P(1/3 < X < 4/3) =Ф(4/3)-Ф(1/3)=0,4082-0,1293=0,2789

Задание 10.

Непрерывная случайная величина Х распределена равномерно на интервале [а; b]. Найти плотность распределения случайной величины Y=g(Х), математическое ожидание M(Y) и дисперсию D(Y) случайной величины Y

№ вар	а	b	Y

18	0	2	объем куба с
			ребром Х

Решение. Непрерывная случайная величина Х распределена равномерно на интервале [0; 2], ее плотность постоянна на этом интервале и равна нулю вне его, т.е.

	1		, a x b
				.

f (X ) b a
0,		x a, x b

		1	,0 x 2
Имеем			,0 x 2
Имеем	f (X )	2
	0,		x 0, x 2

Так как на рассматриваемом промежутке функция Y=X3 строго возрастающая, то плотность q(y) будем искать по формуле

q(y)=f( (y)) | ’(y)|

где (y)= 3 y - функция, обратная функции Y=x3. Подставляя (y)= 3 y и

																	33 y2
																	33 y2
учитывая, что\| ’(y)\| =											3	y					1		, получим
											3

	1			,0 y	8
	1

			2
			2
q( y) 63 y
		y 0, y 8
0,		y 0, y 8
Найдем искомое математическое ожидание
8						8		1					4		8
8						8		1					4		8
M (Y) yq(y)dy					1	y3dy						1 y3					2
0					6	0						8			0
0						0									0
Найдем искомую дисперсию
8					M (Y)					2 1			8			4				1	7	8	36
8													8			4					7	8
D(Y) y2q(y)dy													y			3 dy 4					y3	4
D(Y) y2q(y)dy													y			3 dy 4					y3	4
0												6	0					14				0	7
0					1								0									0
					1				,0	y 8
																					1
Ответ:						y	2
							2
	q(y) 63													;M(Y)=2;D(Y)=5 /7
						y 0, y 8
				0,		y 0, y 8

Задание 11.

По заданной плотности распределения fХ (х) случайной величины Х найти функцию распределения FУ (у) случайной величины Y = (Х). Функция Y = (Х) и плотность распределения fХ (х) заданы в таблице:

№ вар	fХ (х)		Y= (Х)

18		1	e X 2
		chx

Решение. Так как в интервале (−∞;+∞ ) функция Y e X 2 не монотонна, то разобьѐм этот интервал на интервалы (−∞;0)и (0; +∞), в которых она моно-

тонна. В интервале (−∞;0) обратная функция ψ1 (y) = ln

, в интервале

(0; +∞)

ψ2 (y) = ln

, ψ’1 (y) =

, ψ’2 (y) =-

;

2y ln

2ye

f(ψ1 (y))= f(ψ2(y)) =

1 y

1 e

Искомую плотность распределения находим из равенства

2ye

gY (y)= f(ψ1 (y)) |ψ’1 (y)|+ f(ψ2 (y)) |ψ’2 (y)|=

1 y

Найдем

функцию распределения FУ(у)

FY x P Y x P e x2 x , где Ф(х)- функция Лапласа, а т.к. у=х при х>0, то

FY y y . FУ (у)

Ответ

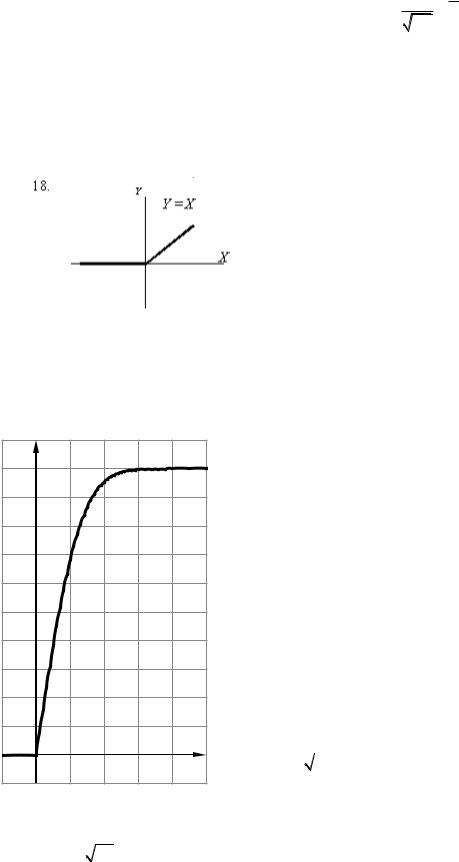
Задание 12.

1 x2

По заданной плотности распределения fX (x) 2 e 2 случайной величины Х

найти функцию распределения FУ(у) случайной величины Y = (Х).

Построить график функции распределения, найти выражение и для плотности fY (y) случайной величины Y . Функция Y = (Х) задана графически

Решение. Аналитически функция Y = (Х) задается так

		Y x					0, x 0
		Y x
							x, x 0
	1,1												Сначала найдем функцию распределения FУ(у)
													FY x P Y x x , где Ф(х)- функция Лапласа, а

	1
	1												т.к. у=х при х>0, то									FY y y . Построим график
	0,9
	0,9
	0,8												(используя значения функции Лапласа из таблиц)
	0,8

	0,7												Найдем	плотность							fY (y) случайной			величины	Y.
	0,7
	0,6
													Функция		Y=x					строго возрастает				при x>0,	то

	0,5
													плотность fY (y) равна

	0,4
	0,4


	0,3												fY (y)= f ( (y))						(y)
	0,2												но x (y) находится из уравнения y=x, то (y) y
	0,2												но x (y) находится из уравнения y=x, то (y) y
	0,1												f ( (y))	1			y2			;			1
	0,1													1			y2
																		2
																		2
	0														2	e					( y)
-	1	0			1	2		3			4	5			2
-	1	0			1	2		3			4	5
	-0,1												Получаем плотности fY (y) случайной величины Y
													Получаем плотности fY (y) случайной величины Y
						1				y2
			f (y)						e 2		, у>0
			f (y)						e 2		, у>0
				Y		2
						2

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.05.201522.02 Кб27Рецензия КП (КР).doc
#
10.05.201532.26 Кб38РЕЦЕНЗИЯ на курсовую работу.doc
#
16.03.2016577.02 Кб9Рецепты доктора Мериголда.doc
#
07.11.2018202.75 Кб11РЕЧЕВАЯ КУЛЬТУРА ДЕЛОВОГО РАЗГОВОРА.doc
#
10.05.2015309.76 Кб15Реш.КРЗ.экспл и наладка.doc
#
10.05.2015720.15 Кб192решение 18 вариант.pdf
#
15.08.20191.53 Mб11Решение прикладных задач обработки данных средс...doc
#
12.11.20191.18 Mб29рим XI-XVII.doc
#
01.12.2018653.31 Кб7Римское право (Буреев).doc
#
10.05.201578.02 Кб5Римское право Бордуков Антон.docx
#
19.04.201989.76 Кб4римское право.docx