
решение 18 вариант
.pdf
Задание 1.
18.На 10 карточках написаны различные цифры от 0 до 9. Найти вероятность того, что наудачу образованное с помощью карточек трехзначное число делится на 50.
Решение. Чтобы трехзначное число, образованное с помощью карточек, делится на 50, оно должно оканчиваться на 50 (других вариантов нет, так карточек с цифрой 0 – одна и она должна стоять последней)
Формируем трехзначное число слева направо: вероятность того, что первая цифра не 5 или 0 8/10, вероятность того, что вторая цифра 5 – 1/9,
вероятность того, что третья цифра 0 – 1/8.
Тогда искомая вероятность равна
p 108 19 81 901
Аналогичный результат получаем, если начинаем формировать число справа налево, вероятности в этом случае будут равны 1/10, 1/9, 1, а искомая вероятность
p 101 19 1 901
Ответ: 1/90

Задание 2.
18.Цех производит 95 % стандартных изделий, причем 90 % из них первого сорта.
Найти вероятность того, что среди трех случайно отобранных изделий хотя бы одно первого сорта.
Решение. Пусть событие А – деталь первого сорта, событие A - деталь не первого сорта. Вероятность того, что деталь первого сорта равна p(А)
=0,95 0,90=0,855 или 85,5%, тогда вероятность того, что деталь не первосортная q=Р( A )= 1-p=0,145.
Найдем вероятность события B= A A A - того, что среди трех случайно отобранных изделий нет ни одного первого сорта. Так как события независимы, то
P(B)=Р( A A A )=Р( A )Р( A )Р( A )=0,1453 0,00305
Событие C, состоящее в том, что среди трех случайно отобранных изделий хотя бы одно первого сорта, противоположно событию В. Тогда его вероятность равна равна
P(C) = 1 - P(B) = 0,99695
Ответ: вероятность того, что среди трех случайно отобранных изделий хотя бы одно первого сорта
0,99695.
Задание 3.
18. На склад поступают детали с трех станков. Вероятность выпуска брака на первом станке 0,03, на втором 0,02, на третьем 0,01.
Производительность первого станка в три раза больше производительности второго, а третьего в два раза больше второго. Найти вероятность того, что:
1)наудачу взятая со склада деталь будет бракованной;
2)она произведена на втором станке.
Решение.
Введем обозначения событий: А – наугад выбранная единица -
бракованная.
Введем следующие предположения(гипотезы) об изготовлении детали:
В1 – произведенная деталь изготовлена 1-м станком, В2 – произведенная деталь изготовлена 2-м станком, В3 – произведенная деталь изготовлена 3-м
станком. Если второй станок производит х деталей, то первый - 3х деталей, а
третий -2х деталей. Поскольку всего имеется три гипотезы, вероятность первой три раза больше, чем во второй, а третей в 2 раза больше чем второй,и
сумма вероятностей гипотез равна единице(так как они образуют полную группу событий), то вероятность каждой из гипотез равна соответственно
Р(В1) = 3/6=1/2, Р(В2) = 1/6, Р(В3) = 2/6=1/3.
Условная вероятность того, что деталь будет бракованной, если она изготовлена 1-м станком, PB1 (A) =0,03.
Условная вероятность того, что деталь будет бракованной, если она изготовлена 2-м станком, PB2 (A) =0,02.
Условная вероятность того, что деталь будет бракованной, если она
изготовлена 3-м станком, PB3 (A) =0,01.
1)Вероятность того, что наугад выбранная единица окажется бракованной, по формуле полной вероятности равна

Р(А) = Р(В ) P (A) +Р(В ) P (A) +Р(В |
) P (A) = |
||||
1 |
B1 |
2 |
B2 |
3 |
B3 |
=1/2 0,03+1/6 0,02+1/3 0,01= 60013 =0,0217
2)Вероятность того, что взятая наугад деталь будет бракованной и изготовлена на втором станке по формуле Бейеса равна
|
|
1 |
0,02 |
|
|||
P (B ) |
P(B2 )PB2 (A) |
|
6 |
0,154 |
|||
P(A) |
|
13 |
|
|
|||
A 2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
600 |
|
|
|
Ответ: 1) 0,0217; 2) 0,154.
Задание 4.
18. Батарея дала 14 выстрелов по военному объекту с вероятностью
попадания в него, равной 0,2. Найти
1)наивероятнейшее число попаданий и его вероятность;
2)вероятность разрушения объекта, если для этого требуется не менее
4 попаданий.
Решение. По условию, n = 14,р = 0,2, q = 1-p=0,8.
1) Найдем наивероятнейшее число ko из двойного неравенства np - q k0 < nр + р.
Подставив данные задачи, получим
14 0,2- 0,8 k0 < 14 0,2 + 0,2, или 2 k0 <3.
Так как k0—целое число и поскольку между числами 2 k0 <3
заключено одно целое число, а именно 2, то искомое наивероятнейшее число k0=2.
2)Число испытаний небольшое. Воспользуемся формулой Бернулли для нахождения вероятности 0, 1,2 и 3 попаданий. Суммируя эти значения, получим вероятность не разрушения объекта, а
вероятность противоположного события и даст вероятность разрушения объекта
P (0) |
0 |
0, 20 |
0,814 |
0,814 0,04398 |
||
14 |
|
|
C14 |
|
|
|
P (1) |
|
1 |
0, 2 0,813 14 0, 2 0,813 0,15393 |
|||
14 |
|
C14 |
|
|
|
|
P (2) |
2 |
0, 22 |
0,812 |
91 0,04 0, 4 0, 25014 |
||
14 |
|
|
C14 |
|
|
|
P (3) |
|
3 |
0, 23 |
0,811 |
364 0,008 0, 4 0, 25014 |
|
14 |
|
|
C14 |
|
|
|
P P |
(0) P (1) P (2) P (3) 0,04398 0,15393 0, 25014 0, 25014 0,6982 |
|||||
14 |
|
|
|
14 |
14 |
14 |
Вероятность того, что в объект будет произведено менее 4
попаданий равно 0,6982. Тогда вероятность того, что в объект будет произведено не менее 4 попаданий равно 0,3018
Ответ: 1) 2; 2) 0,3018.
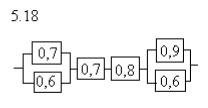
Задание 5.
В технической системе дублированы не все, а только некоторые
(наименее надежные) узлы. Надежности (вероятности безотказной работы)
узлов проставлены на рисунках. Найти надежность всей системы.
1 2
Решение. Рассмотрим части системы, соединенные параллельно.
Рассмотрим узел 1 системы. Вероятность выхода из строя этого узла равна произведению вероятностей выхода из строя входящих в него частей и равна (1-0,7)(1-0,6)=0,3 0,4=0,12. Тогда вероятность безотказной работы этого узла равна 1-0,12=0,88.
Аналогично, для узла 2 получаем надежность (вероятности безотказной работы) равную 1-0,1 0,4=0,96
Рассмотрим части системы, соединенные последовательно.
Вероятность безотказной работы в этом случае находится как произведение вероятностей входящих в систему частей и равна
P=0,88 0,7 0,8 0,96=0,473
Ответ: надежность всей системы равна 0,473.

Задание 6.
6.18.а) Найти закон распределения случайной величины Х:
Испытывается устройство, состоящее из трех независимо работающих блоков. Вероятности отказа блоков таковы: р1 = 0.3, р2 = 0,5, р3= 0,6. Х -
число отказавших блоков.
Решение. a) q1=1 - р1 = 0,7, q2=1 - р2 = 0,5, q3=1 - р3= 0,4
Введем обозначения событий: А – первый блок работает без отказов, B– второй блок работает без отказов, С– третий блок работает без отказов.
P(A)=0,3; P(B)=0,5; P(C)=0,6; тогда P( A )=0,7; P( B )=0,5; P( C )=0,4 X=0, это событие ABC. События A, B, C независимы
P(ABC)= P(A) P(B) P(C)=0,3 0,5 0,6=0,09
X=1, это событие A BC+ A B C+ AB C , события A BC, A B C, AB C не совместны.
P( A BC+ A B C+ AB C )= P( A BC) +P(A B C) +P(AB C )= =0,7 0,5 0,6+0,3 0,5 0,6+0,3 0,5 0,4=0,21+0,09+0,06=0,36
X=2, это событие A B C + A B C + A B C, события A B C , A B C , A B C не
совместны.
P(A B C + A B C + A B C)= P(A B C ) +P( A B C ) +P( A B C)= =0,3 0,5 0,4+0,7 0,5 0,4+0,7 0,5 0,6=0,06+0,14+0,21=0,41
X=3, это событие A B C .
P( A B C )=P( A )P( B )P( C )=0,14
Закон распределения случайной величины Х имеет вид
X |
0 |
1 |
2 |
3 |
|
|
|
|
|
P |
0,09 |
0,36 |
0,41 |
0,14 |
|
|
|
|
|
Контроль: 0,09+0,36+0,41+0,14=1
б). Случайная величина Х задана рядом распределения
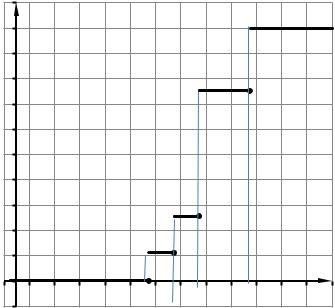
1) Найти функцию распределения F(х) случайной величины Х и построить ее график.
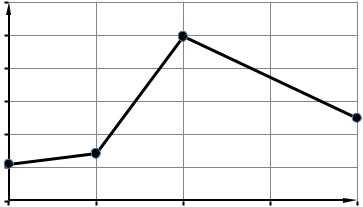
2) Найти математическое ожидание М(Х) и дисперсию D(X) случайной
величины Х, построить многоугольник распределения.
Значения параметров х1, х2, х3, х4, р1, р2, р3, р4 вычислить по следующим формулам: N- номер варианта;
R=остаток(N/4)+2=4;
х1= N+3=21;х2= х1+ R =25;х3= х2+ R =29;х4= х3+ 2R =37;
p |
1 |
|
1 ; |
p |
1 |
|
|
1 |
; p |
1 |
|
1 |
; p |
|
41 33R R2 |
R3 |
|
|
125 |
; |
||
1 |
R 5 |
9 |
2 |
R 3 |
|
7 |
4 |
8 R |
|
4 |
3 |
|
R 3 R 5 8 R |
|
252 |
|
||||||
Решение. Закон распределения случайной величины Х имеет вид |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
21 |
|
|
|
|
|
25 |
|
|
|
|
29 |
|
37 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P |
|
|
|
1/9 |
|
|
|
|
|
1/7 |
|
|
|
|
125/252 |
|
1/4 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контроль: 1/9+1/7+125/252+1/4=1
1) Найходим функцию распределения F(х) случайной величины Х Если x 21, то F(x)=P(X < x)=0;
eсли 21<x 25, то F(x)=P(X < x)= 1/9;
eсли 25<x 29, то F(x)=P(X < x)= 1/9+1/7=16/63;
eсли 29<x 37, то F(x)=P(X < x)= 1/9+1/7+125/252=189/252; eсли x>37, то F(x)=P(X < x)= 1/9+1/7+125/252+1/4=1
Построим ее график
1,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
2 |
6 |
10 |
14 |
18 |
22 |
26 |
30 |
34 |
38 |
42 |
46 |
50 |
-0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Построим вспомогательную таблицу
xi |
21 |
25 |
29 |
37 |
Сумма |
|
|
|
|
|
|
pi |
1/9 |
1/7 |
125/252 |
1/4 |
1 |
|
|
|
|
|
|
xipi |
2,33 |
3,57 |
14,38 |
9,25 |
29,54 |
|
|
|
|
|
|
xi2 |
441 |
625 |
841 |
1369 |
|
|
|
|
|
|
|
xi2pi |
49,00 |
89,29 |
417,16 |
342,25 |
897,70 |
|
|
|
|
|
|
Математическое ожидание дискретной случайной величины есть сумма |
||||
произведений еѐ возможных значений на их вероятности: |
||||
|
|
n |
|
|
|
M (X ) xi |
pi ; M(X)=29,54 |
|
|
|
|
i 1 |
|
|
Дисперсия дискретной случайной величины есть математическое ожидание |
||||
квадрата отклонения случайной величины от еѐ математического ожидания |
||||
|
|
D(X ) M[X M(X )]2 |
|
|
Дисперсию удобно считать по формуле |
|
|||
D(X ) M(X 2 ) [M(X )]2 ; D(X)= 897,70-29,542 =25,11 |
|
|||
Построим многоугольник распределения. |
|
|||
3/5 |
|
|
|
|
1/2 |
|
|
|
|
2/5 |
|
|
|
|
3/10 |
|
|
|
|
1/5 |
|
|
|
|
1/10 |
|
|
|
|
0 |
|
|
|
|
21 |
25 |
29 |
33 |
37 |
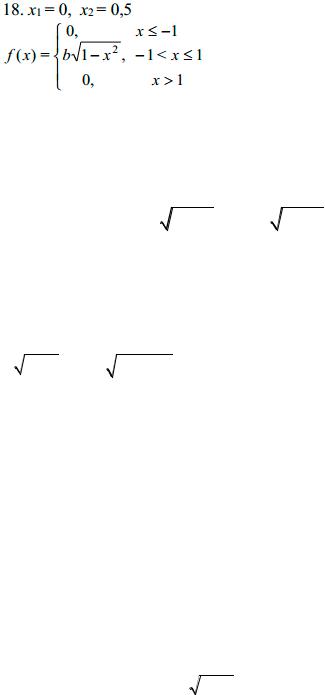
Задание 7а. Непрерывная случайная величина Х подчинена закону
распределения с плотностью f(x). Требуется:
1)найти коэффициент b;
2)найти интегральную функцию распределения F(x);
3)построить графики функций f(x) и F(x);
4)найти математическое ожидание М(Х), дисперсию D(X) и (Х)
случайной величины Х и вероятность попадания CВ Х в интервал (х1, х2).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Находим параметр b из условия: |
|
|
|
f (x)dx 1. Так как все значения |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
случайной величины заключены на отрезке [-1;1], то |
|
|||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
1 f (x)dx b |
1 x2 |
dx b |
1 x2 dx. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
Положим x=siny, тогда dx=cosydy. Если |
x-1, то y = - /2, |
если x=1, |
||||||||||||||||||||||||||
то y = /2. Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
1 cos 2y dy |
|
|
|
|
1 x2 |
dx |
1 sin2 y |
|
cos ydy cos2 |
|
ydy |
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|
|
1 |
y |
1 |
sin 2y |
|
2 |
|
|
|
|
|||||||
|
|
dy |
|
|
cos 2yd2y |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
4 |
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда, |
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Находим интегральную функцию распределения |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
Используем формулу F(x) f (x)dx. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
Если x≤-1, то f(x)=0, следовательно, F(x) 0dx 0 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||
Если -1<x≤1, то f(x)= |
|
1 x2 , следовательно, |
|
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
