
MathCadTV 5semestr
.pdfЗадачи по теории вероятностей в MathCADе 1. Функции и инструменты MATHCAD
Прежде чем приступать к решению задач теории вероятностей в MathCAD, познакомимся с инструментами, которые предоставляет пакет для их решения.
Напомним, что дискретная случайная величина , принимающая значения x1 < x2 < … < xi <… с вероятностями p1, p2, … pi, …, может быть задана распределением — таблицей вида
|
x1 |
x 2 |
… |
x i |
… |
x n |
P |
p 1 |
p 2 |
… |
p i |
… |
p n |
Такие таблицы в среде MathCAD удобно хранить в виде матрицы размерности 2 х n
Функция распределения случайной величины, имеющей приведенное выше распределение, имеет вид
|
0, |
|
|
x x1 |
|
|
|||
|
p , |
|
|
x |
|
x x |
2 |
|
|
|
1 |
|
|
1 |
|
|
|
||
F(x) |
p1 p2 , |
|
x2 x x3 |
|
|||||
.................. |
|
...... |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
p p |
... p |
, |
x |
n 1 |
x x |
n |
||
|
1 2 |
n 1 |
|
|
|
|
|||
|
1, |
|
|
x |
n |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ниже приведен фрагмент рабочего документа с определением распределения случайной величины, ее функции распределения и графиком функции распределения для случайной величины, имеющей следующее распределение:
|
1 |
0 |
7 |
4 |
-2 |
|
P |
0.1 |
0.5 |
0.1 |
0.1 |
0.2 |
|
|
|
|
|
|
|
|
Распределение случайной величины |
||||||
ORIGIN 1 |
A |
|
2 |
0 |
1 |
4 |
7 |
||
|
0.2 |
0.5 |
0.1 |
0.1 |
0.1 |
||||
|
|
|
|||||||
Функция распределения случайной величины |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
F(x) |
0 if |
x A1 1 |
|
|
|
|
|
|
|
|
A2 1 if A1 1 x A1 2 |
|
|
|
|
|
|
||
|
A2 1 A2 2 if A1 2 x A1 3 |
|
|
|
|
||||
|
A2 1 A2 2 A2 3 if A1 3 x A1 4 |
|
|
||||||
|
A2 1 A2 2 A2 3 A2 4 |
if A1 4 x A1 5 |
|||||||
|
1 if |
A1 5 x |
|
|
|
|
|
|
|
Функция распределения случайной величины, определенная другим образом

G(x) |
|
0 if x 2 |
|
|
|
|
||
|
|
|
|
|
||||
|
|
0.2 |
if 2 x 0 |
|
|
|
|
|
|
|
0.2 |
0.5 |
if 0 x |
1 |
|
|
|
|
|
0.2 |
0.5 |
0.1 if |
1 |
x |
4 |
|
|
|
0.2 |
0.5 |
0.1 0.1 |
if |
4 |
x 7 |
|
|
|
1 if 7 x |
|
|
|
|
||
|
|
|
|
|
|
|||
График функции распределения случайной величины
1.1 |
1 |
1.1 |
1 |
|
|
|
|
||
F(x) |
0.5 |
|
|
G(x) |
0.5 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
4 |
3 |
2 |
1 |
0 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 10 |
5 |
4 |
3 |
2 |
1 |
0 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 10 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
10 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
10 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Указание. Распределение случайной величины сохранено в матрице А: A1,i — значения случайной величины; А2,i — соответствующие вероятности; i = 1, 2, 3, 4, 5. Функцию распределения, заданную разными выражениями на разных интервалах изменения аргументов, можно определить следующим образом: разверните панель программных
элементов щелчком по кнопке  и панель знаков отношений – щелчком по кнопке
и панель знаков отношений – щелчком по кнопке  и не закрывайте их, пока не закончите определение функции. Введите имя функции переменной х и знак присваивания, щелкните в панели программных элементов по кнопке
и не закрывайте их, пока не закончите определение функции. Введите имя функции переменной х и знак присваивания, щелкните в панели программных элементов по кнопке
 , введите в помеченной позиции нуль, щелкните по кнопке
, введите в помеченной позиции нуль, щелкните по кнопке  и введите неравенства, определяющие первый интервал изменения аргумента (символ можно ввести
и введите неравенства, определяющие первый интервал изменения аргумента (символ можно ввести
щелчком по соответствующей кнопке в панели  ); затем перейдите во вторую строку определения функции, введите A2,1 – имя переменной, содержащей значение p1, или число 0.2 - значение p1, выделите, нажимая клавишу <Space>, выражение для функции, щелкните
); затем перейдите во вторую строку определения функции, введите A2,1 – имя переменной, содержащей значение p1, или число 0.2 - значение p1, выделите, нажимая клавишу <Space>, выражение для функции, щелкните
по кнопке  , введите неравенства, определяющие второй интервал изменения аргумента (знак можно ввести щелчком по соответствующей кнопке в панели отношений); выделите, нажимая клавишу <Space>, вторую строку определения функции, щелкните по кнопке
, введите неравенства, определяющие второй интервал изменения аргумента (знак можно ввести щелчком по соответствующей кнопке в панели отношений); выделите, нажимая клавишу <Space>, вторую строку определения функции, щелкните по кнопке
 , и введите, действуя, как описано выше, определение функции на следующем интервале.
, и введите, действуя, как описано выше, определение функции на следующем интервале.
В рабочем документе приведены два способа определения функции — с использованием имен переменных и с использованием конкретных значений этих переменных. Графики функций распределений построены стандартным для декартовых графиков способом. Следует помнить, что Mathcad не совсем корректно строит графики ступенчатых функций, соединяя отрезками прямых значения функции в точке скачка. Более точный график функции распределения представляет собой отрезки, параллельные оси абсцисс, с
"выколотым" правым концом.
Распределение дискретного случайного вектора
|
y1 |
y2 |
… |
y3 |
|
|
|
|
|
x1 |
p11 |
p12 |
… |
p1m |
|
|
|
|
|
x2 |
P21 |
p22 |
… |
p2n |
|
|
|
|
|
… |
… |
… |
… |
… |
|
|
|
|
|
xm |
pm1 |
pm2 |
… |
pmn |
|
|
|
|
|
также удобно хранить в матрице размерности (т +1) x (n + 1). Первому элементу первой строки этой матрицы присваивается нулевое значение, остальные элементы первой строки содержат значения случайной компоненты , элементы первого столбца — значения
случайной компоненты , а остальные элементы — соответствующие вероятности: элемент, расположенный в (j+1)-м столбце (i+1)-й строки содержит значение вероятности pij того, что случайный вектор ( , ) принимает значение (xi , yj).
Ниже приведен фрагмент рабочего документа MathCAD с определением распределения дискретного случайного вектора, заданного следующей таблицей:
|
1 |
3 |
5 |
7 |
2 |
0.01 |
0.01 |
0.17 |
0.01 |
4 |
0.1 |
0.2 |
0.1 |
0.2 |
6 |
0.02 |
0.05 |
0.09 |
0.04 |
0 |
1 |
3 |
5 |
7 |
|
|
2 |
0.01 |
0.01 |
0.17 |
0.01 |
|
|
p |
|
|
|
|
|
|
|
4 |
0.1 |
0.2 |
0.1 |
0.2 |
|
|
|
|
|
|
|
|
6 |
0.02 |
0.05 |
0.09 |
0.04 |
|
|
Для вычислений со случайными величинами (непрерывными и дискретными) в MathCAD есть богатая библиотека встроенных функций наиболее распространенных стандартных распределений. Каждое распределение представлено в библиотеке тремя функциями — плотностью вероятностей, функцией распределения и функцией, обратной к функции распределения.
Например, для работы с нормальным распределением предназначены функции dnorm(x, , ), pnorm(x, , ) и qnorm(x, , ). Значением функции dnorm(x, , ) является значение в точке х плотности вероятностей случайной величины , имеющей нормальное распределение с математическим ожиданием М = и дисперсией D = 2; значение функции pnorm(x, , ) — значение функции распределения этой же случайной величины ; значением функции qnorm(x, , ) служит решение уравнения F(x) = р, где F(x) — функция распределения, определенная функцией pnorm(x, , ), т.е. значением qnorm(x, , ) является квантиль уровня р нормально распределенной случайной величины. Имена всех встроенных функций, определяющих плотности вероятностей, начинаются с буквы d, определяющих функции распределения — с буквы р, определяющих квантили — с буквы q.
Ниже приведены список всех распределений, представленных в библиотеке MathCAD, и имена соответствующих функций:
бета-распределение — dbeta (x,s1,s2), pbeta(x,s1,s2), qbeta(x,s1,s2); биномиальное распределение — dbinom(k,n,p), pbinom(k,n,p), qbinom(p,n,r); распределение Коши — dcauchy(x,l,s), pcauchy(x,l,s), qcauchy(p,l,s);
2 распределение — dchisq(x,d), pchisq(x,d), qchisq(p,d);
экспоненциальное распределение — dexp(x,r), pexp(x,r), qexp(p,r); распределение Фишера (F-распределение) — dF(x,d1,d2), pF(x,d1,d2), qexp(x,d1,d2)
гамма-распределение — dgamma(x,s), pgamma(x,s), qgamma(p,s);
геометрическое распределение — dgeom(x,p), pgeom(x,p), qgeom(p,r);
логнормальное распределение — dlnorm(x, , ), plnorm(x, , ), qlnorm(x, , );
логистическое распределение — dlogis(x,l,s), plogis(x,l,s), qlogis(p,l,s);
отрицательное биномиальное распределение — dnbinom(k,n,p), pnbinom(k,n,p), qnbinom(p,n,r);
нормальное распределение — dnorm(x, , ), pnorm(x, , ), qnorm(x, , );
распределение Пуассона — dpois(x, ), ppois(x, ), qpois(p, ); распределение Стьюдента — dt(x,d), pt(x,d), qt(p,d);
равномерное распределение — dunif(x,a,b), punif(x,a,b), qunif(p,a,b); распределение Вейбулла — dweibull(x,s), pweibull(x,s), qweibull(p,s).
Ниже приведены графики и вычисления, демонстрирующие некоторые свойства функций, связанных со стандартным нормальным распределением N(0,1).
p(x) dnorm(x 0 1) |
|
Плотность вероятностей |
|
|
|
|
|
|
|
|||||||||||||
F(x) pnorm(x 0 1) |
|
Функция распределения |
|
|
|
|
|
|
|
|||||||||||||
q(x) qnorm(x 0 1) |
|
Обратная к функции распределения |
||||||||||||||||||||
1 |
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
p(x) |
0.5 |
|
|
|
|
|
F(x) |
|
|
|
0.5 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.487 10 6 |
|
|
|
|
|
|
|
2.867 10 7 |
|
|
|
|
|
|
|
|
|
|
||||
5 |
0 |
5 |
|
|
5 |
0 |
5 |
|||||||||||||||
|
|
5 |
|
x |
5 |
|
|
5 |
|
x |
5 |
|||||||||||
a qnorm(0.1 0 1) |
|
a 1.282 |
|
|
pnorm(a 0 1) |
0.1 |
||||||||||||||||
Кроме того, в библиотеке встроенных функций MathCAD, естественно, есть функция
|
2 |
|
x |
|
Лапласа erf x = |
|
e t2 dt . Для вычисления числовых характеристик дискретных и |
||
|
|
|
||
|
|
|||
|
|
0 |
||
|
|
|
||
непрерывных случайных величин применяются операторы интегрирования и дифференцирования, вычисления конечных сумм и суммирования рядов, которые
вызываются щелчком мыши по кнопке в панели 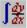 и заполнением соответствующих помеченных полей. Примеры использования этих операций при решении задач теории вероятностей приведены в последующих разделах этой главы.
и заполнением соответствующих помеченных полей. Примеры использования этих операций при решении задач теории вероятностей приведены в последующих разделах этой главы.
2. Случайные величины. функции распределения
Теория вероятностей изучает математические модели случайных явлений окружающего нас мира. Одно из центральных понятий теории вероятностей — понятие случайной величины.
Случайной величиной называется числовая функция, заданная на множестве случайных событий.
Например, случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело с дискретной случайной величиной (она принимает значения из дискретного числового множества) М = {1, 2, 3, 4, 5, 6}; во втором случае — с непрерывной случайной величиной (она принимает значения из непрерывного числового множества — из промежутка числовой прямой I = [100, 230]). В дальнейшем случайные величины будем обозначать греческими буквами.
Функция распределения случайной величины
Каждая случайная величина полностью определяется своей функцией распределения.
Если — случайная величина, то функция F(x) = F (x) = P( <x) называется функцией распределения случайной величины . Здесь P( <x) — вероятность того, что случайная величина принимает значение, меньшее x.
Функция распределения любой случайной величины обладает следующими свойствами:
F(x) определена на всей числовой прямой R;
|
F(x) не убывает, т.е. если x1 x2, то F(x1) F(x2); |
|
|
F(- ) = 0 и F(+ )=1, т.е. limF(x) 0 |
и limF(x) 1 |
|
x |
x |
|
F(x) непрерывна слева, т.е. limF(x) F(x0 ) |
|
|
x x0 0 |
|
Важно понимать, что функция распределения является "паспортом" случайной величины: она содержит всю информацию об этой случайной величине, и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением. Так что когда говорят о нормальном распределении, то подразумевают случайную величину, имеющую нормальную функцию распределения. В дальнейшем будем использовать термин распределение.
У дискретной случайной величины функция распределения ступенчатая. Например, в приведенном ниже фрагменте рабочего документа Mathcad определена функция распределения числа очков, выпавших при одном бросании игральной кости.
|
|
|
|
|
|
|
|||||||||
F(x) |
0 |
if |
x 1 |
|
|
|
|||||||||
|
|
1 |
if |
|
1 x 2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
6 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
1 |
if |
|
2 x 3 |
||||||||
|
|
|
|
|
|
||||||||||
|
|
6 |
6 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
1 |
|
1 |
if 3 x 4 |
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
6 |
6 |
6 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
1 |
|
1 |
|
1 |
if 4 x 5 |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
6 |
6 |
6 |
6 |
||||||||||
|
|
|
|
|
|
|
|||||||||
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
if 5 x 6 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
6 |
|
6 |
|
6 |
|
6 |
6 |
|||||||
|
|
if |
6 x |
|
|
|
|||||||||
|
1 |
|
|
|
|
||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0.83 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(x) |
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0.33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0.17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
7 |
|||||
Указание. Следует отметить, что MathCAD, изображая ступенчатые функции, соединяет отрезком прямой значения функций в точках разрыва. Разрывные функции принято изображать иначе — помечая стрелкой направление разрыва (стрелка вправо — функция непрерывна в точке справа, стрелка влево — для точек, где функция непрерывна слева). На рис. 5.1 приведен график функции распределения в общепринятом виде.
Если функция распределения F (x) непрерывна, то случайная величина называется непрерывной случайной величиной. Если функция распределения F (x) непрерывно дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины p (x), которая связана с функцией распределения F (x) формулами
F (x)= |
x |
p (t)dt и |
p (x) |
dF (x) |
|
dx |
|||
|
|
|
||
|
|
|
||
Рис. 5.1. График функции распределения, исправленный в графическом редакторе
Отсюда, в частности, следует, что для любой случайной величины p (x)dx 1
Если — дискретная случайная величина, принимающая значения x1, x2, … , xi, … с вероятностями p1, p2, …, pi …, то таблица вида
|
x1 |
x2 |
… |
xi |
… |
р |
p1 |
p2 |
… |
pi |
… |
называется рядом распределения дискретной случайной величины или просто распределением дискретной случайной величины. В практических задачах именно такая форма представления распределения наиболее удобна.
Вероятность того, что значение случайной величины попадает в интервал (а, b), вычисляется для непрерывной случайной величины по формуле
b
P(a b) F (b) F (a) p (t)dt ,
a
а для дискретной случайной величины — по формуле
P(a b) pi .
xi (a,b)
Наиболее распространенные распределения дискретных случайных величин
Познакомимся с дискретными случайными величинами, которые чаще всего используются при решении практических задач со случайными величинами, имеющими биномиальное, геометрическое, гипергеометрическое и пуассоновское распределения.
Биномиальное распределение (схема Бернулли). Пусть проводится серия из p
независимых испытаний, каждое из которых заканчивается либо "успехом", либо "неуспехом". Пусть в каждом испытании (опыте) вероятность успеха p, а вероятность неудачи — q = 1 — р. С таким испытанием можно связать случайную величину , равную числу успехов в серии из n испытаний. Эта величина принимает целые значения от 0 до n. Ее распределение называется биномиальным и определяется формулой Бернулли
p P( k) Ck pk qn k , |
|||||
k |
|
n |
|
||
|
|
n! |
n |
||
где 0 p 1, q = 1 - p, k = 0, 1, …, n |
Сnk |
. Нетрудно убедиться, что pk 1 |
|||
|
|
||||
k!(n k)! |
|||||
|
|
k 0 |
|||
В MathCAD для вычисления плотности вероятности и функции распределения случайной величины, имеющей биномиальное распределение, предназначены функции dbinom(k,n,p) и pbinom(k, n,p), значения которых — соответственно pk и F(k).
Геометрическое распределение. Со схемой испытаний Бернулли можно связать еще одну случайную величину: — число испытаний до первого успеха. Эта величина принимает бесконечное множество значений от 0 до + , и ее распределение определяется формулой
pk P( k) qk p , k = 0, 1,…, 0 < p < 1, q = 1 – p.
Используя формулу суммы бесконечно убывающей геометрической прогрессии, легко показать, что
В MathCAD для вычисления плотности вероятности и функции распределения случайной величины, имеющей геометрическое распределение, предназначены функции dgeom(k,p) и pgeom(k, р), значения которых — соответственно pk и F(k).
Гипергеометрическое распределение. Пусть в партии из N изделий имеется М (М < N)
доброкачественных и (N — M) дефектных изделий. Если случайным образом из всей партии выбрать контрольную партию из п изделий, то число доброкачественных изделий в этой партии будет случайной величиной, которую обозначим . Ее распределение имеет вид:
p P( k) |
Ck |
Cn k |
|
M |
N M |
, k = 0, 1, …, min (n, M), |
|
|
|
||
k |
Cn |
||
|
|
N |
|

и называется гипергеометрическим. Для любых значений параметров, входящих в
min(n,M ) |
|
распределение параметров, pk |
1. |
k 0
ВMathCAD нет встроенных функций для вычисления плотности
вероятности и функции распределения случайной величины, имеющей гипергеометрическое распределение. При необходимости эти функции можно определить по приведенным выше формулам.
Пуассоновское распределение. Пуассоновское распределение имеет случайная величина , принимающая значения k = 0, 1, 2, ... с вероятностями
pk P( k) k e , k = 0, 1, 2, … , k!
где > 0 — параметр пуассоновского распределения. При любых > 0. pk 1.
k 0
В MathCAD для вычисления плотности вероятности и функции распределения случайной величины, имеющей пуассоновское распределение, предназначены функции dpois(k, ) и ppois(k, ), значения которых — соответственно pk и F(k).
Задание 1
Постройте
1)биномиальное распределение для серии из п независимых испытаний с вероятностью успеха р,
2)пуассоновское распределение с параметром ,
3)гипергеометрическое распределение с параметрами N, М, п,
4)геометрическое распределение с параметрами п, р.
5)распределение Паскаля с параметрами п, р.,r
Для каждого распределения выполните следующее: проверьте равенство pk 1, где pk =
(k)
P(Х = k); найдите значение k, для которого величина Р(X = k) максимальна; постройте графики распределения и функций распределения;вычислите вероятность попадания значений случайной величины в интервал (а,b).
№ |
п |
p |
|
N |
М |
п |
а |
b |
|
|
|
|
|
|
|||
|
Бин.Геом |
Пуас |
Гипергеометрическое |
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
20 |
0.1 |
1.00 |
100 |
90 |
20 |
2 |
4 |
2 |
22 |
0.11 |
0.95 |
110 |
100 |
22 |
3 |
5 |
3 |
24 |
0.12 |
0.90 |
120 |
100 |
24 |
2 |
5 |
4 |
26 |
0.13 |
0.85 |
130 |
120 |
26 |
3 |
6 |
5 |
28 |
0.14 |
0.80 |
140 |
120 |
28 |
2 |
5 |
6 |
30 |
0.15 |
0.75 |
150 |
120 |
30 |
3 |
6 |
7 |
21 |
0.16 |
0.70 |
160 |
150 |
21 |
2 |
8 |
8 |
23 |
0.17 |
0.65 |
170 |
150 |
23 |
3 |
9 |
9 |
25 |
0.18 |
0.60 |
180 |
160 |
25 |
2 |
7 |
10 |
27 |
0.19 |
0.55 |
190 |
180 |
27 |
3 |
8 |
11 |
29 |
0.20 |
0.50 |
200 |
150 |
29 |
3 |
10 |
12 |
31 |
0.21 |
1.05 |
105 |
100 |
31 |
4 |
10 |
13 |
20 |
0.22 |
1.10 |
115 |
100 |
20 |
3 |
5 |
14 |
22 |
0.23 |
1.15 |
125O |
100 |
22 |
4 |
6 |
15 |
24 |
0.24 |
1.25 |
135 |
110 |
24 |
3 |
6 |
16 |
26 |
0.25 |
1.30 |
145 |
120 |
26 |
4 |
7 |
17 |
28 |
0.26 |
1.35 |
155 |
120 |
28 |
3 |
7 |
18 |
30 |
0.27 |
1.40 |
165 |
150 |
30 |
4 |
8 |
19 |
21 |
0.28 |
1.45 |
175 |
170 |
21 |
03 |
10 |
20 |
23 |
0.29 |
1.50 |
185 |
170 |
23 |
4 |
11 |
|
|
|
|
|
|
|
|
|
Порядок выполнения задания
1.Введите параметры распределения.
2.Определите интервал изменения значений случайной величины.
3.Определите вектор, номера компонент которого равны значениям случайной величины, и присвойте компонентам вектора значения вероятности соответствующих значений.
4.Определите функцию распределения случайной величины.
5.Постройте графики распределения и функции распределения случайной величины.
6.Найдите по графику наиболее вероятное значение случайной величины.
7.Введите в рабочий документ наибольшее значение вероятности (значение вероятности в точке, вычисленной в предыдущем пункте).
8.Вычислите сумму всех значений вероятностей.
9.Вычислите вероятность попадания значения случайной величины в указанный интервал как разность соответствующих значений функции распределения.
10.Измените значения параметров распределения и повторите вычисления. Сравните полученные результаты.
11.Выполните вычисления пп. 1-10 для всех приведенный в задании распределений.
Пример выполнения задания
Постройте биномиальное распределение для серии из 20 независимых испытаний с вероятностью успеха р = 0.4, 0.6, 0.8. Постройте графики распределения и функций распределения. Для р = 0.4 найдите значение k, для которого величина Р( = k} максимальна. Проверьте равенство pk 1. Вычислите вероятность попадания значений
k
случайной величины в интервал (1, 5).
Постройте пуассоновское распределение с параметром = 0.2, 0.4, гипергеометрическое распределение для N = 30, М = 10, n = 10 геометрическое распределение с такими же
параметрами, что и биномиальное (р = 0.4). Проверьте равенство pk 1. Постройте
k
графики распределения и функций распределения. Вычислите вероятность попадания значений случайной величины в интервал (1,5) для всех распределений, кроме гипергеометрического. Вычислите вероятность попадания значений случайной величины, имеющей гипергеометрическое распределение, в интервал (1,2). Для каждого распределения найдите значение k, для которого величина Р( = k) максимальна.
Фрагмент рабочего документа, содержащий вычисления для биномиального распределения, приведен ниже.
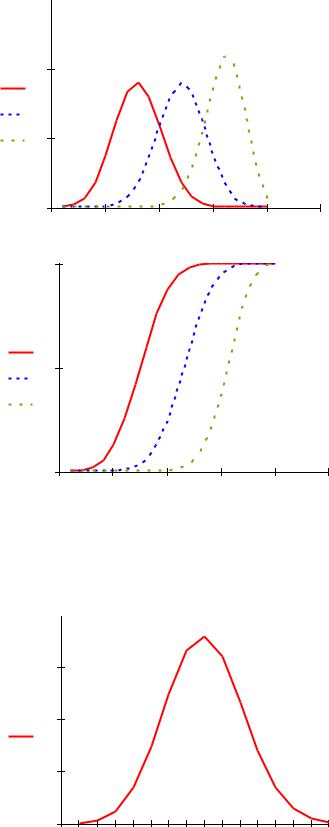
k 1 20 |
|
|
|
|
|
|
||
P 4k dbinom(k 20 0.4) |
|
|
F4k pbinom(k 20 0.4) |
|||||
P 6k dbinom(k 20 0.6) |
|
|
F6k pbinom(k 20 0.6) |
|||||
P 8k dbinom(k 20 0.8) |
|
|
F8k pbinom(k 20 0.8) |
|||||
P 4k |
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P 6k |
|
|
|
|
|
|
|
|
P 8k |
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
0 |
5 |
|
10 |
15 |
20 |
25 |
|
|
|
|
|
|
k |
|
|
|
|
1 |
|
|
|
|
|
|
F4k |
|
|
|
|
|
|
|
|
F6k |
0.5 |
|
|
|
|
|
|
|
F8k |
|
|
|
|
|
|
|
|
|
|
0 |
5 |
|
10 |
15 |
20 |
25 |
|
|
|
|
|
|
k |
|
|
20 |
|
|
|
|
|
|
|
|
|
P 4 1 |
|
F4 F4 |
0.125 |
P 4 0.18 |
|||
|
k |
|
5 |
1 |
|
|
8 |
|
k 1 |
|
|
|
|
|
|
|
|
|
0.15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P 4k |
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
