
lec_08-03-01_2014
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Кафедра физики
Колмаков Ю.Н.
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
"Физика"
Для направления подготовки: 08.03.01 Строительство
Форма обучения очная
Тула - 2014
2
Конспект лекций подготовлен к.ф.-м.н. проф. Ю.Н. Колмаковым, обсужден на заседании кафедры физики естественнонаучного факультета протокол № 1 от «_29_» _августа_ 2014 г.
Зав. кафедрой физики ___________ Д.М. Левин
3
ОГЛАВЛЕНИЕ |
|
1. ВВЕДЕНИЕ |
|
Физика как наука. Роль физики в развитии техники. Связь физики с математикой. Общая структура |
|
и задачи курса физики. ……………………………………………………………………………………………………… |
стр.7 |
2. КИНЕМАТИКА |
|
2.1. Системы отсчета. Скалярные и векторные физические величины ………………………………………….…7 |
|
2.2. Разложение произвольного движения физического тела на поступательное и вращательное движение…...7 2.3. Кинематика поступательного движения в трехмерном пространстве. Перемещение, скорость, ускорение..7 2.4. Применение производных и интегралов в кинематике произвольного движения…………………………….8
2.5. Кинематика криволинейного поступательного движения. Нормальное и тангенциальное ускорение………9
2.6. Кинематика вращательного движения вокруг закрепленной оси. Угловая скорость и угловое ускорение…9 2.7. Связь линейных и угловых кинематических переменных………………………………………………………10
3. ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ 3.1. Импульс материальной точки (частицы). Разновидности сил в классической механике…………………….11
3.2. Инерциальные системы отсчета. Законы Ньютона в инерциальных системах………………………………..12 3.3. Центр масс системы материальных точек (физического тела). Уравнение движения центра масс…………13
3.4. Неинерциальные системы отсчета и уравнения динамики поступательного движения в неинерциальных системах отсчета……………………………………………………………………………………………14
3.5. Реактивное движение. Сила тяги и уравнение Мещерского…………………………………………………….15
4. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ВОКРУГ ЗАКРЕПЛЕННОЙ ОСИ
4.1.Момент силы и момент импульса материальной точки…………………………………………………………16
4.2.Момент импульса системы материальных точек (физического тела)………………………………………….16
4.3.Момент инерции материальной точки и физического тела. Примеры вывода момента инерции симметричных тел. Теорема Штейнера……………………………………………………………………16
4.4.Тензор момента инерции и главные оси инерции……………………………………………………………….17
4.5.Основное уравнение динамики вращательного движения вокруг закрепленной оси…………………………18
5. ЗАКОНЫ СОХРАНЕНИЯ
5.1.Закон сохранения и изменения импульса физической системы………………………………………………..19
5.2.Закон сохранения и изменения момента импульса физической системы.…………………………………….20
5.3.Работа силы при поступательном и работа момента сил при вращательном движении. Мощность………..20
5.4.Консервативные и неконсервативные силы. Диссипативные силы……………………………………………20
5.5.Потенциальная энергия частицы и системы частиц. Потенциальная энергия в поле сил тяжести
ипотенциальная энергия упругого взаимодействия………………………………………………………………………….21
5.6.Кинетическая энергия поступательного и вращательного движения………………………………………….22
5.7.Закон сохранения и изменения полной механической энергии………………………………………………..23
5.8.Плоское движение и законы сохранения…………………………………………………………………………23
6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
6.1.Кинематические характеристики колебательного процесса (амплитуда, фаза, частота). Условие возникновения гармонических колебаний………………………………………………………………………….24
6.2.Одномерный гармонический осциллятор (пружинный маятник). Связь характеристик колебания
сначальными условиями………………………………………………………………………………………………………...25
6.3.Физический и математический маятник…………………………………………………………………………..25
6.4.Связь энергии гармонического осциллятора и амплитуды его колебаний……………………………………..26
6.5.Свободные затухающие колебания. Зависимость амплитуды и периода затухающих колебаний от коэффициента затухания. Критическое затухание. Логарифмический декремент………………………………………26
6.6.Сложение взаимно-перпендикулярных и однонаправленных колебаний. Метод векторной диаграммы……28
6.7.Вынужденные колебания. Зависимость амплитуды и начальной фазы
вынужденных колебаний от частоты……………………………………………………………………………………………29
6.8.Резонанс и резонансные частоты…………………………………………………………………………………...30
6.9.Характеристики волнового процесса. Длина волны, волновой вектор и фазовая скорость волны.
Плоские и сферические волны. …………………………………………………………………………………………………31
6.10.Упругие волны в сплошных средах. Бегущие и стоячие волны. Явление технической реверберации………32
7. ОСНОВЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ
7.1.Преобразования Галилея и принцип относительности Галилея. Экспериментальные факты,
противоречащие классической механике……………………………………………………………………………………….33
7.2.Принцип относительности Эйнштейна. Постулаты Эйнштейна………………………………………………..34
7.3.Преобразования Лоренца и их следствия…………………………………………………………………………34
7.4.Релятивистское замедление времени и релятивистское сокращение длины…………………………………..35
7.5.Релятивистский импульс и полная энергия релятивистской частицы. Связь релятивистского импульса и полной энергии……………………………………………………………………………………………………..35
7.6.Энергия покоя. Дефект масс……………………………………………………………………………………….36
8. ОСНОВЫ ТЕРМОДИНАМИКИ 8.1. Термодинамический и молекулярно-кинетический способы описания. Термодинамические параметры….37
4
8.2.Термодинамические процессы: равновесный и неравновесный, обратимый и необратимый.
Основное (нулевое) начало термодинамики…………………………………………………………………………………..37
8.3.Идеальный газ и уравнение состояния идеального газа……………………………………………………….38
8.4.Уравнения изопроцессов в идеальном газе……………………………………………………………………..38
8.5.Внутренняя энергия термодинамической системы (идеального газа) и работа по изменению её объема….39
8.6.Теплоемкость термодинамической системы (идеального газа) при различных изопроцессах……………....40
8.7.Первое начало термодинамики. Уравнение первого начала термодинамики для идеального газа…………40
8.8.Адиабатный и политропный процессы. Уравнение Пуассона…………………………………………………40
9. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ЭНТРОПИЯ 9.1. Термодинамическое определение энтропии. Изменение энтропии при различных изопроцессах………….41
9.2. Частные формулировки второго начала термодинамики. Невозможность существования вечных двигателей 1-го и 2-го рода…………………………………………………………………………………………….41
9.3. Изменение энтропии при необратимых процессах. Общая формулировка второго начала термодинамики..42 9.4. Циклические процессы. Цикл Карно……………………………………………………………………………...42 9.5. К.п.д. циклических процессов (тепловых машин). Холодильник, кондиционер, тепловой насос…………...43
9.6. Макро- и микросостояние системы. Термодинамическая вероятность………………………………………..44 9.7. Статистическое определение энтропии (формула Больцмана)…………………………………………………45
9.8. Третье начало термодинамики……………………………………………………………………………………45
10. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
10.1.Функция распределения и её смысл. Функция распределения Гаусса для случайных величин…………….46
10.2.Распределение Максвелла молекул по проекциям и по величинам скоростей.
Экспериментальная проверка распределения Максвелла…………………………………………………………………….47
10.3.Средние скорости молекул газа………………………………………………………………………………….48
10.4.Частота соударений молекул газа о стенку сосуда……………………………………………………………..49
10.5.Внутренняя энергия и теплоемкость в молекулярно-кинетической теории…………………………………49
10.6.Идеальный газ в поле внешних сил. Барометрическая формула………………………………………………50
10.7.Распределение Больцмана……………………………………………………………………………………….51
11. КИНЕТИЧЕСКИЕ ЯВЛЕНИЯ (ПРОЦЕССЫ ПЕРЕНОСА) В ГАЗАХ
11.1.Столкновения молекул газа между собой. Эффективное сечение взаимодействия молекул
исредняя длина свободного пробега молекулы……………………………………………………………………………….51
11.2.Рассеяние пучка молекул в газе…………………………………………………………………………………52
11.3.Явления переноса в идеальном газе. Поток переносимой величины…………………………………………52
11.4.Теплопроводность. Коэффициент теплопроводности…………………………………………………………53
11.5.Диффузия. Коэффициент диффузии…………………………………………………………………………….54
12.МЕХАНИКА ЖИДКИХ И ГАЗООБРАЗНЫХ СРЕД
12.1.Идеальная несжимаемая жидкость………………………………………………………………………………55
12.2.Стационарное течение жидкости (газа). Уравнение неразрывности. Уравнение Бернулли…………………55
12.3.Вязкость газа. Динамический коэффициент вязкости. Сила вязкого трения…………………………………56
12.4.Ламинарное и турбулентное течение газообразной или жидкой среды. Критерий Рейнольдса……………56
12.5.Течение вязкого газа (жидкости) по трубе. Формула Пуазейля……………………………………………….57
13.КОНДЕНСИРОВАННОЕ СОСТОЯНИЕ
13.1.Межмолекулярное взаимодействие……………………………………………………………………………...57
13.2.Агрегатные состояния: кристаллическое, аморфное, жидкое и газообразное………………………………..58
13.3.Уравнение состояния реального газа…………………………………………………………………………….59
13.4.Поверхностное натяжение. Смачивание и несмачивание. Краевой угол……………………………………...60
13.5.Капиллярные явления. Формула Лапласа. Осмос………………………………………………………………61
13.6.Упругие деформации и напряжения. Закон Гука. Пластические деформации. Предел прочности…………62
14. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
14.1.Термодинамические фазы и компоненты. Условие равновесия фаз…………………………………………..63
14.2.Фазовые переходы первого рода…………………………………………………………………………………64
14.3.Процессы испарения и конденсации. Центры конденсации…………………………………………………...65
14.4.Процессы плавления и отвердевания. Центры кристаллизации……………………………………………….68
15. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ
15.1.Поле покоящегося точечного заряда. Напряженность и потенциал поля. Принцип суперпозиции.
Поле системы покоящихся зарядов. Сила Кулона…………………………………………………………………………….69
15.2.Работа по перемещению заряда в электростатическом поле………………………………………………….70
15.3.Связь напряженности и потенциала электростатического поля. Силовые линии
иэквипотенциальные поверхности…………………………………………………………………………………………….71
15.4.Поток вектора напряженности. Теорема Гаусса для вектора напряженности электростатического поля…72
15.5.Применение теоремы Гаусса для расчета напряженности: поле равномерно заряженного шара,
провода (нити), плоскости………………………………………………………………………………………………………72
15.6.Теорема Гаусса для электростатического поля в дифференциальной форме………………………………..74
15.7.Теорема о циркуляции вектора напряженности электростатического поля…………………………………74
15.8.Электрический диполь. Энергия диполя в электрическом поле, действующая на него сила и момент сил..74
5
16. ПРОВОДНИК В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 16.1. Поверхностные заряды. Поле вблизи границы заряженного проводника…………………………………..76
16.2. Явление электрической индукции. Экранировка поля проводящим слоем. Электростатическая защита…77 16.3. Электрическая ёмкость проводника. Конденсаторы и ёмкость конденсаторов……………………………..77 16.4. Энергия взаимодействия системы электрических зарядов. Энергия заряженного конденсатора………….79
17. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИЧЕСКИХ СРЕДАХ 17.1. Причины поляризации диэлектриков. Вектор поляризованности. Объемные и поверхностные
связанные заряды………………………………………………………………………………………………………………..80
17.2.Диэлектрическая проницаемость среды и вектор электрической индукции………………………………..81
17.3.Теорема Гаусса для векторов поляризованности и электрической индукции………………………………81
17.4.Электрическое поле в диэлектрике……………………………………………………………………………..82
17.5.Поле на границе диэлектрика. Граничные условия для векторов напряженности
иэлектрической индукции………………………………………………………………………………………………………83
17.6.Плотность энергии электростатического поля в диэлектрике………………………………………………..83
18.СТАЦИОНАРНЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
18.1.Сила тока и плотность тока……………………………………………………………………………………..84
18.2.Уравнение непрерывности электрического заряда и условие стационарности тока……………………….85
18.3.Электрическое поле в проводнике с током и закон Ома в локальной форме………………………………...85
18.4.Причина затухания тока. Электрическое сопротивление проводника. Законы Ома и Джоуля-Ленца…….86
18.5.Условие квазистационарности тока…………………………………………………………………………….87
18.6.Причины появления электродвижущей силы. Источники ЭДС………………………………………………88
18.7.Закон Ома для неоднородного участка цепи…………………………………………………………………..88
18.8.Разветвленные электрические цепи. Правила Кирхгофа и их применение………………………………….89
19.ПОСТОЯННОЕ МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ
19.1.Причина появления магнитного поля. Вектор индукции магнитного поля…………………………………90
19.2.Сила Лоренца…………………………………………………………………………………………………….91
19.3.Магнитное поле движущегося электрического заряда и элемента тока. Закон Био-Савара-Лапласа……..92
19.4.Сила Ампера………………………………………………………………………………………………………93
19.5.Теорема Гаусса для индукции магнитного поля……………………………………………………………….94
19.6.Теорема о циркуляции вектора индукции магнитного поля…………………………………………………..94
19.7.Применение теоремы о циркуляции к расчету магнитного поля: поле цилиндрического провода
стоком, поверхностного тока, соленоидальной и тороидальной катушки с током…………………………………………95
19.8.Теорема о циркуляции вектора индукции в дифференциальной форме……………………………………..96
19.9.Сравнение особенностей электростатического и магнитостатического полей………………………………97
19.10.Движение заряженной частицы в постоянных магнитном и электрическом полях………………………...97
19.11.Дипольный магнитный момент контура с током……………………………………………………………...98
19.12.Энергия замкнутого проводника с постоянным током во внешнем магнитном поле.
Сила и момент силы, действующие на контур с током……………………………………………………………………….98
20. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ 20.1. Намагничение среды и вектор намагниченности………………………………………………………………99
20.2. Магнитная проницаемость среды и вектор напряженности магнитного поля………………………………100
20.3. Теорема о циркуляции вектора напряженности и вектора намагниченности………………………………..101 20.4. Магнитное поле в магнетиках. Поле постоянного магнита…………………………………………………...102 20.5. Поле на границе магнетика. Граничные условия для векторов напряженности
и индукции магнитного поля…………………………………………………………………………………………………..103 20.6. Причины появления диа-, пара- и ферромагнетизма………………………………………………………….104
21. ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
21.1.Природа ЭДС электромагнитной индукции в проводниках, движущихся в магнитном поле. Принцип действия электромотора и генератора электрического тока……………………………………………………..105
21.2.Вихревое электрическое поле и причина его появления……………………………………………………..106
21.3.Закон Фарадея и правило Ленца………………………………………………………………………………..107
21.4.Проводник и постоянный магнит в переменном магнитном поле. Индукционные токи (токи Фуко)……107
21.5.Коэффициент индуктивности. Индуктивность соленоида…………………………………………………..108
21.6.Плотность энергии магнитного поля…………………………………………………………………………..109
21.7.Явление самоиндукции и ЭДС самоиндукции………………………………………………………………..109
21.8.Явление взаимной индукции. Коэффициенты взаимной индуктивности
ипринцип действия трансформатора…………………………………………………………………………………………110
22. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
22.1.Электрический колебательный контур. Собственные электрические колебания в контурах (незатухающие и затухающие), их характеристики…………………………………………………………………………111
22.2.Вынужденные электрические колебания………………………………………………………………………112
22.3.Резонанс напряжения на конденсаторе и тока в контуре. Добротность контура…………………………..113
22.4.Полное сопротивление (импеданс) контура. Эффективные ток и напряжение…………………………….114
6
23. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ И ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
23.1.Ток смещения……………………………………………………………………………………………………115
23.2.Система уравнений Максвелла……………………………………………………………………………….116
23.3.Поток плотности энергии электромагнитного поля. Вектор Пойнтинга и теорема Пойнтинга………….117
23.3.Волновое уравнение для электромагнитного поля в идеальном диэлектрике (вакууме)………………….119
23.4.Электромагнитные волны. Волновой вектор. Скорость электромагнитных волн. Связь напряженности электрического и магнитного поля в электромагнитной волне…………………………………………119
23.5.Шкала электромагнитных волн………………………………………………………………………………120
23.6.Энергия и импульс электромагнитной волны………………………………………………………………..121
23.7.Излучение электромагнитных волн ускоренными зарядами. Волновая зона………………………………122
24. ВОЛНОВЫЕ ПРОЦЕССЫ
24.1.Суперпозиция электромагнитных волн. Условие когерентности и возникновение интерференции…….123
24.2.Оптическая разность хода. Условия максимума и минимума при интерференции……………………….124
24.3.Интерференционная схема Юнга…………………………………………………………………………….124
24.4.Интерференция в тонких пленках……………………………………………………………………………..126
24.5.Принцип Гюйгенса-Френеля…………………………………………………………………………………..127
24.6.Дифракция света на узкой щели и круглом препятствии. Условие дифракционного минимума………...127
24.7.Многолучевая интерференция. Дифракционная решетка и принцип спектрометрии.
Критерий Рэлея. Разрешающая способность дифракционной решетки…………………………………………………..130
24.8.Поляризация электромагнитных волн. Поляризаторы и закон Малюса……………………………………131
25. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
25.1.Характеристики теплового излучения. Энергетическая светимость, излучательная
ипоглощательная способность………………………………………………………………………………………………...134
25.2.Закон Стефана-Больцмана и закон смещения Вина для теплового излучения абсолютно черного тела. Коэффициент поглощения…………………………………………………………………………………….134
25.3.Неприменимость законов классической физики. Гипотеза Планка…………………………………………136
26. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ МИКРОЧАСТИЦ
26.1. Фотон. Энергия и импульс фотона…………………………………………………………………………….137
26.2. Внешний и внутренний фотоэффект. Уравнение Эйнштейна для фотоэффекта. Работа выхода электрона из металла и красная граница фотоэффекта………………………………………………………………………137
26.3. Эффект Комптона……………………………………………………………………………………………….138
26.4. Гипотеза де Бройля. Волна де Бройля…………………………………………………………………………138
26.5. Опыты по дифракции микрочастиц…………………………………………………………………………….139
26.6. Корпускулярно-волновой дуализм…………………………………………………………………………….139
27. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ АТОМА 27.1. Планетарная модель атома. Постулат Бора. Боровские электронные орбиты в одноэлектронном
атоме. Спектр энергии одноэлектронного атома…………………………………………………………………………….140
27.2. Излучение одноэлектронного атома. Спектральные серии Лаймана, Бальмера, Пашена………………….141
27.3. Орбитальный момент импульса и орбитальный магнитный момент электрона в атоме.
Орбитальное и магнитное квантовые числа…………………………………………………………………………………..142 27.4. Опыты Штерна-Герлаха…………………………………………………………………………………………142
27.5. Собственный момент импульса и собственный магнитный момент электрона.
Спиновое квантовое число……………………………………………………………………………………………………..143
27.6.Система четырех квантовых чисел и принцип Паули………………………………………………………..143
27.7.Заполнение электронами оболочек и подоболочек в атоме…………………………………………………..144 28. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ МИКРОСИСТЕМ
28.1.Опыт с прохождением микрочастицы через двухщелевую диафрагму. Волновая функция………………145
28.2.Вероятностный смысл волновой функции. Квантовый принцип суперпозиции…………………………...146
28.3.Принцип неопределенности Гейзенберга. Соотношения неопределенности и их смысл………………….146
28.4.Стационарное уравнение Шредингера………………………………………………………………………...148
28.5.Микрочастица в одномерной потенциальной яме прямоугольной формы………………………………….148
28.6.Туннельный эффект……………………………………………………………………………………………..149
28.7.Квантовый гармонический осциллятор………………………………………………………………………..150 29. ОСНОВЫ ТЕОРИИ АТОМНОГО ЯДРА
29.1.Состав атомного ядра. Нуклоны. Массовое и зарядовое число. Изотопы………………………………….150
29.2.Деление ядер……………………………………………………………………………………………………..151
29.3.α-, β- и γ-излучение. α- и β-распад ядер………………………………………………………………………..151
29.4.Естественная радиоактивность. Закон радиоактивного распада. Период полураспада……………………153
29.5.Энергия выхода ядерной реакции распада. Дефект масс…………………………………………………….154
29.6.Удельная энергия связи нуклонов в ядре. Устойчивость и неустойчивость ядер.
Возможность термоядерного синтеза…………………………………………………………………………………………154
7
1. ВВЕДЕНИЕ Физика как наука. Роль физики в развитии техники. Связь физики с математикой. Общая струк-
тура и задачи курса физики
2. КИНЕМАТИКА 2.1. Системы отсчета. Скалярные и векторные физические величины
Классическая механика изучает механическое движение частиц (материальных точек) и тел, т.е. изменение положения их в пространстве с течением времени.
Частица (материальная точка) – это тело, размерами которого в условиях данной задачи можно пренебречь. Одно и то же тело в различных условиях либо может считаться частицей, либо – нет.
Другая абстракция – абсолютно твердое тело – это система частиц, расстояния между которыми в процессе движения тела остаются неизменными.
При этом постулируется, что:
1)пространство является бесконечным, однородным (все точки его одинаковы), изотропным (все свойства пространства одинаковы во всех направлениях), а свойства пространства не зависят от находящихся в нем тел;
2)время является однородным, течет только в одном направлении, и ход времени не зависит от состояния движения
тел.
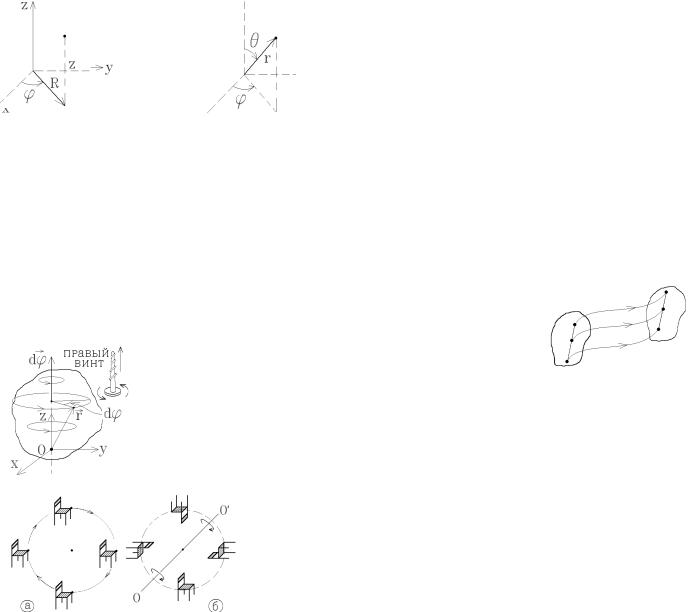
Так как все точки пространства одинаковы, то определить, изменили ли частица (тело) положение или нет, возможно только по отношению к какому-либо другому телу, называемому телом отсчета. Обычно с телом отсчета связывают некоторую систему координат: декартову, цилиндрическую, сферическую (см.рисунок).
Совокупность системы пространственных координат, жестко связанной с телом отсчета, и системы отсчета времени называется системой отсчета. Система отсчета времени представляет собой со-
вокупность синхронизованных часов, находящихся в каждой точке системы координат. Понятие синхронизованные означает: "одинаково идущие". Механическое движение тел рассматривается в выбранной системе отсчета.
2.2. Разложение произвольного движения физического тела на поступательное и вращательное движение
Рассматривают несколько видов движений абсолютно твердого тела: поступательное, вращательное движение вокруг оси (в частности, – закрепленной), плоское движение, вращательное движение вокруг точки и свободное движение. Первые два вида – основные: любое движение твердого тела можно свести к поступательному движению и вращению относительно некоторой оси.
Поступательным движением называется такое движение, при котором все точки тела движутся по одинаковым траекториям, или, иначе говоря, любая прямая, связанная с телом, перемещается параллельно самой себе (рисунок справа).
При вращении вокруг закрепленной оси все точки движутся по соосным окружностям (рисунок слева). За время dt происходит поворот тела на угол d ϕ . Поэтому вместо линейных характеристик
вводятся угловые характеристики: поворот тела на бесконечно малый угол d ϕ характеризуется вектором угла поворота d ϕ , направленным по оси вращения по правилу правого винта.
Пример: движение стула на рис. а не будет вращательным. Это поступательное криволинейное движение по окружности, когда все точки тела движутся по одинаковым траекториям, но положение центра кривизны для них различно. На рис.б изображено вращательное движение стула: все его точки описывают окружности вокруг общей оси вращения ОО', но радиусы этих
окружностей различны.
Любое произвольное движение физического тела или системы материальных точек можно представить в виде суммы двух простых движений: поступательного и вращательного.
2.3. Кинематика поступательного движения в трехмерном пространстве. Перемещение, скорость, ускорение
Существуют различные способы определения положения частицы. В первую очередь это векторный способ опи-
сания движения.
В этом случае положение частицы задается её радиус-вектором r . Геометрическое место концов радиус-вектора представляет кривую, называемую траекторией. Зависимость радиус-вектора частицы от времени r = r (t) называется кинематическим законом движения. С геометрической точки зрения – это уравнение траектории.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
Изменение радиус-вектора |
r |
за время t называется перемещением: |
r = r |
− r . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
Очевидно, что перемещение (вектор!) совпадает по величине с хордой, проведенной из |
|||||||||||||||||||
|
|
|
|
|
точки 1 в точку 2 (см.рисунок). Длина дуги траектории между этими точками |
l называ- |
||||||||||||||||||
|
|
|
|
|
ется путем. Для бесконечно малого временного интервала dt |
соответствующее беско- |
||||||||||||||||||
|
|
|
|
|
нечно малое (в дальнейшем – элементарное) перемещение dr |
направлено по касатель- |
||||||||||||||||||
|
|
|
|
|
ной к траектории в точке 1. Модуль элементарного перемещения равен элементарному |
|||||||||||||||||||
|
|
|
|
|
пути: |
|
dr |
|
= dl. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
Важнейшей кинематической характеристикой движения является скорость. Скоро- |
|||||||||||||||
стью частицы называется векторная величина, определяемая равенством |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = lim |
r = |
dr |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t→0 |
t |
|
dt |
|
|
|
|
|
иначе говоря, скорость – это производная от радиус- |
вектора по времени |
. |
|
|
|
|||||||||||||||||||
Из определения следует, что скорость v направлена по касательной к траектории (см.рисунок). Величина скорости |
||||||||||||||||||||||||
|
v = |
|
v |
|
= |
|
dr |
|
= |
dl |
, |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
dt |
|
|
dt |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где l - путь, пройденный вдоль траектории. Иногда используется понятие средней скорости: это векторная величина,
равная отношению перемещения ко времени, т.е. |
v = |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
||
Производная скорости частицы по времени, т.е. вектор |
t |
|
|
|
|
|
||
v |
|
dv |
|
d 2r |
||||
|
= lim |
= |
= |
|||||
a |
|
|
|
|
||||
t |
dt |
dt |
2 |
|||||
|
t→0 |
|
|
|||||
называется ускорением частицы. О направлении вектора a и о его величине a = a разговор пойдет чуть позже.
2.4. Применение производных и интегралов в кинематике произвольного движения
Таким образом, зная кинематический закон движения, можно простым дифференцированием по времени найти скорость и ускорение в любой момент времени (так называемая прямая задача кинематики). Наоборот, зная ускорение час-
тицы, а также начальные условия, т.е. положение r и скорость v |
частицы в начальный момент времени t |
0 |
= 0 , можно |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
найти траекторию движения частицы r (t) |
(обратная задача кинематики). Действительно, dv = a dt |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
и dr |
= vdt , поэто- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
му |
|
v(t) = v0 |
+ ∫ adt , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и далее: |
|
|
|
|
|
|
|
r (t) = r0 + ∫vdt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если с телом отсчета жестко связать какую-нибудь координатную систему (например, декартову), то положение |
||||||||||||||||||||||||||||||||||||||
частицы в любой момент времени определяется тремя ее координатами x, |
y, z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Проектируя радиус-вектор на координатные оси, получим три зависимости коорди- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
нат частицы от времени |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = x(t) , y = y(t), z = z(t) , |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
которые представляют кинематический закон движения в координатной форме. Из рисун- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ка видно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
= xi |
+ yj |
+ zk , |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
- единичные векторы, |
или орты декартовой системы координат. Отсюда не- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
где |
i , |
|
j , |
k |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
медленно следует принцип независимости движений: произвольное движение частицы |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
можно рассматривать как сумму независимых движений по координатным осям x, y, z. . |
||||||||||||||||||||||||||||
|
Зная формулы для векторов скорости и ускорения частицы, можно найти их проекции на координатные оси: |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
= |
dx |
, vy = |
dy |
vz = |
dz |
|
|
|
|
|
|
ax = |
dv |
x |
= |
d 2 x |
, ay = |
dvy |
= |
d 2 y |
, az = |
dv |
z |
= |
d 2 z |
|
|
||||||||
|
|
vx |
|
|
|
, |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||||
|
dt |
|
dt |
|
|
dt |
dt2 |
dt |
dt2 |
|
|
|
dt 2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
||||||||||||||
|
Следовательно, модули скорости и ускорения будут |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
v = |
|
|
|
|
|
|
a = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
vx2 + vy2 + vz2 |
|
|
и |
|
ax2 + a2y + az2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Аналогично предыдущему пункту решается и обратная задача:
t |
t |
vx (t) = v0 x + ∫ ax dt |
и x(t) = x0 + ∫ vx (t)dt |
0 |
0 |
и так далее.
9
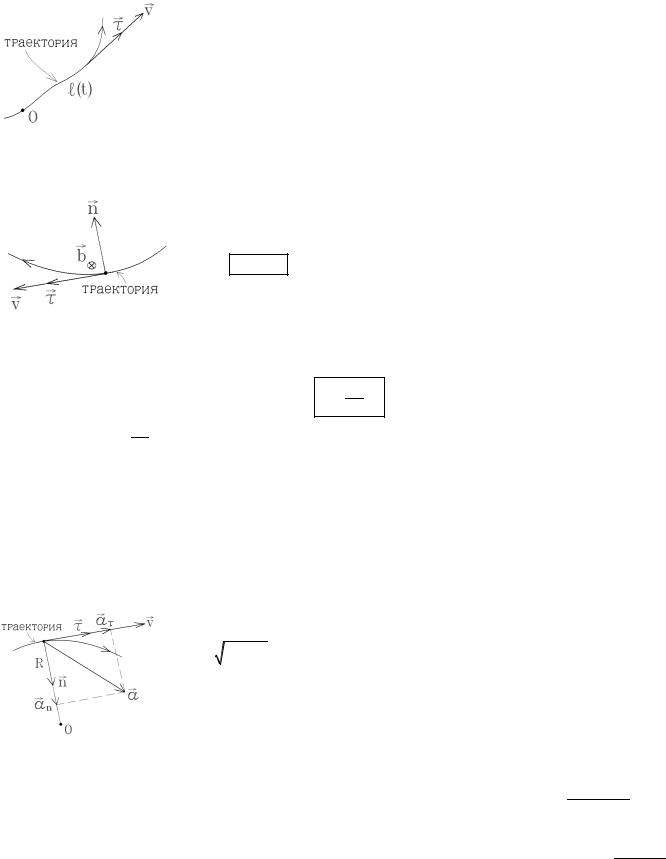
2.5. Кинематика криволинейного поступательного движения. Нормальное и тангенциальное ускорение
Этот способ обычно используется, если известна траектория движения точки. При этом начало отсчета (точка O ) выбирается на траектории, выбирается также положительное направление движения вдоль траектории, а положение частицы описывается криволинейной координатой l(t) , представляющей не что иное, как длину дуги кривой линии, отсчитанной
вдоль траектории от начальной точки O , т.е. путь (см.рисунок).
В этом случае l = l(t) - кинематический закон движения. Из формулы для скорости
t
следует, что dl = v × dt и l = ∫ vdt .
0
Свяжем с траекторией естественную систему координат, состоящую из трех взаимно перпендикулярных осей: касательной (единичный вектор t , направленный вдоль вектора скорости частицы), нормали (единичный вектор n , направ-
ленный к центру кривизны траектории), |
и бинормали |
(единичный вектор |
|
|
] ) |
|||||||
b = [τ, |
n |
|||||||||||
|
b |
и |
|
= |
|
= |
|
= 1. |
|
|
|
|
(см.рисунок). По определению τ n |
τ |
n |
b |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Как следует из этого рисунка, v = v × t .
Чтобы найти ускорение частицы, продифференцируем последнюю формулу по времени, учитывая, что как v , так и t являются функциями времени:
|
|
|
|
d |
|
dv |
|
|
|
|
dv |
|
d τ |
||||||
a |
= |
|
= |
|
(v τ) = |
|
τ + v |
|
. |
dt |
dt |
|
|
||||||
|
|
|
|
dt |
dt |
||||
Первое слагаемое направлено по касательной к траектории и называется тангенциальным (касательным) ускорени-
ем:
aτ = dv τ . dt
Его модуль aτ = dv равен производной от величины скорости по времени, поэтому тангенциальное ускорение ха- dt
рактеризует изменение скорости по величине.
Второе слагаемое направлено по нормали к траектории, характеризует изменение скорости по направлению, назы-
вается нормальным ускорением и определяется выражением: |
|
an = |
v2 |
n. |
|
|
|
||||||
R |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Его модуль an = |
v2 |
. (Заметим, что в случае движения частицы по окружности – |
это хорошо известное центрост- |
||||||||||
R |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
ремительное ускорение.) |
|
|
|
|
|
|
|
|
|
|
|
||
Подведем итоги. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Полное ускорение можно разложить на две составляющие: тангенциальное ускорение |
|||||||||||
|
|
aτ и нормальное ускорение an |
(см.рисунок): a = aτ + an , причем модуль полного ускоре- |
||||||||||
|
|
ния a = |
|
|
. Что касается бинормальной составляющей ускорения, то, как следует из |
||||||||
|
|
a2 |
+ a2 |
||||||||||
|
|
|
τ |
n |
|
|
|
|
|
|
|
||
|
|
предыдущих рассуждений, она тождественно равна нулю. |
|
|
|||||||||
|
|
В частности, при движении частицы по прямой R → ∞ , a = 0 |
и a = a . А при |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
τ |
|
|
|
равномерном движении частицы по окружности aτ = 0 и |
a = an . |
|
|||||||||
2.6. Кинематика вращательного движения вокруг закрепленной оси. Угловая скорость и угловое ускорение
|
|
|
|
|
|
|
|
|
|
d ϕ |
|
|
|
|
|||
Быстрота изменения угла поворота характеризуется вектором угловой скорости |
ω = |
|
, |
|
|
|
|
|
|
|
|
|
|
||||
направленным так же, как и вектор d ϕ , т.е. по оси вращения по правилу правого винта. |
|
dt |
|
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
Еще одна кинематическая характеристика вращательного движения – вектор углового ускорения |
|
|
ε |
= |
dω |
. |
||
|
|
|||||||
|
|
|
|
|
|
|
dt |
|
Вектор углового ускорения совпадает по направлению с вектором угловой скорости при ускоренном вращении и противоположен ему при замедленном вращении.
10
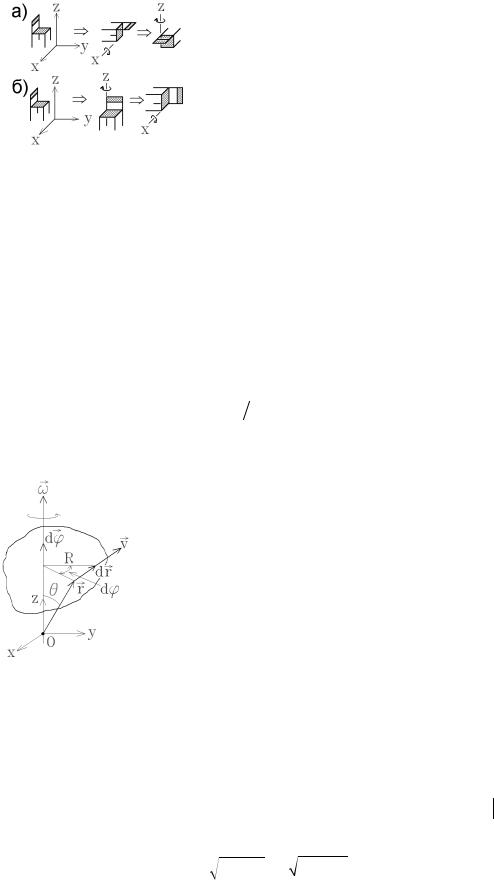
Замечание. Конечный угол поворота не является вектором! Он не подчиняется принципу коммутативности, т.е. результат сложения двух конечных углов поворота (двух последовательных вращений) зависит от порядка слагаемых (от последовательности вращений):
j1 + j2 ¹ j2 + j1 .
В качестве примера рассмотрим два последовательных поворота предмета (стула) по часовой стрелке на угол π / 2 . На рисунке а) изображен вначале поворот стула вокруг оси x , а затем – вокруг оси z . На рисунке б) стул вначале вращают вокруг оси z , а затем – вокруг оси x . Конечные положения стула заметно отличаются друг от друга. Тем не менее, бесконечно малые углы поворота можно склады-
вать векторно:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d j1 |
+ d j2 » dj2 + dj1 , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так как при изменении порядка сложения бесконечно малых векторов результат будет |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отличаться на бесконечно малую второго порядка O((dϕ)2 ) , которой можно пренеб- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
речь. Поэтому векторы угловой скорости и углового ускорения можно складывать |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обычным образом: если тело участвует в двух вращениях, то результирующая угловая |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
скорость равна векторной сумме двух составляющих векторов: ωрез = ω1 + ω2 (то же |
|||||||||||||||||||||||||||||||
самое относится и к угловому ускорению). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
Так же, как и при поступательном движении, при вращательном существуют прямая и обратная задачи кинематики. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
Прямая задача: по заданному как функция времени углу поворота ϕ = ϕ(t) найти ωz и εz ; решается она диффе- |
|||||||||||||||||||||||||||||||||||||||||||||||
ренцированием по времени: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
ω |
z |
= |
dϕ |
= ϕɺ |
, |
|
|
ε |
z |
= |
dωz |
= ωɺ |
z |
= ϕɺɺ . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Обратная задача: по заданному как функция времени угловому ускорению εz = εz (t) и начальным условиям |
|||||||||||||||||||||||||||||||||||||||||||||||
(ωz (t = 0) = ω0 и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ϕ(t = 0) = ϕ0 ) |
найти кинематический закон вращения; она решается с помощью интегрирования: |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωz (t) = ω0 + ∫ εz (t) dt , ϕ(t) = ϕ0 + ∫ ωz (t) dt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда получаются простые формулы равнопеременного вращения ( εz = const ): |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
ω |
z |
= ω + ε |
z |
t , |
ϕ = ϕ + ω t + ε |
z |
|
t2 |
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2.7. Связь линейных и угловых кинематических переменных |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим произвольную точку в твердом теле, которое вращается вокруг закрепленной |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
оси. Установим связь между векторами v и ω . Как следует из рисунка, величина элементарно- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
го перемещения точки (или путь) будет равна |
|
dr |
|
= Rdϕ = r sin θ dϕ , поэтому |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
= [d ϕ |
, r ] , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
т.е. элементарное перемещение равно векторному произведению элементарного угла поворота |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
на радиус-вектор точки. Разделив эту формулу почленно на dt , немедленно получим: |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dr |
|
dϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
, r |
|
или |
v |
|
= [ω, r ] . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда вытекает, что величины линейной и угловой скоростей связаны соотношением: |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
v = |
|
v |
|
= ω r sin θ = ω R , где R – |
расстояние от выделенной точки до оси вращения. |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
Теперь продифференцируем полученную формулу по времени. Это дает: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dv |
|
d ω |
|
|
|
|
dr |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
= |
|
|
|
|
|
|
= |
|
|
|
|
, |
r |
+ |
ω, |
|
|
|
|
|
|
или |
|
a |
|
= [ε, r ] + |
[ω, v |
] . |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
[ε , |
r ] |
|
|
|
|
||||||||||||
|
|
Первое слагаемое направлено по касательной к траектории и равно по модулю |
|
|
= ε r sin θ = ε R – |
это не что |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
иное, как тангенциальное ускорение: aτ = [ε , r ] .
Второе слагаемое направлено по радиусу к центру вращения, равно по модулю
ется нормальным ускорением: |
|
|
|
] |
. Итак: |
|
a |
n |
= ω, [ω, |
r |
|||
|
|
|
|
|
|
|
aτ = ε R , an = ω2 R и a = 
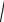 aτ2 + an2 = R
aτ2 + an2 = R
 ε2 + ω4 .
ε2 + ω4 .
|
|
|
|
v2 |
|
|
|
|
|||
[ω, v |
] |
= ω v |
= ω2 R ≡ |
|
и явля- |
|
|||||
|
|
|
|
R |
|
|
|
|
|
||
