
Оглавление
Введение 3
Задача Шредингера о собственных значениях. 4
Задачи о собственных значениях шредингеровского типа. 7
Введение
В недавнее время, в связи с физической теорией квантов, Шредингер натолкнулся на тип задач о собственных значениях, спектр которых обнаруживает совершенно иную структуру, чем рассмотренные до сих пор, а именно состоит из непрерывной из дискретной части, причем дискретный спектр не простирается в бесконечность, но имеет конечную точку сгущения.
Задача Шредингера о собственных значениях.
В простейшей задаче Шредингера речь идет о дифференциальном уравнении
 (1)
(1)
в
пространстве , причем
 обозначает данную положительную
постоянную,
обозначает данную положительную
постоянную, - полярные координаты, а от собственных
функций
- полярные координаты, а от собственных
функций требуется непрерывность в начале
координат и конечно при
требуется непрерывность в начале
координат и конечно при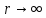 .
Умножая дифференциальное уравнение на
шаровую функцию
.
Умножая дифференциальное уравнение на
шаровую функцию и интегрируя по поверхности единичной
сферы, получим для функции
и интегрируя по поверхности единичной
сферы, получим для функции

обычным образом дифференциальное уравнение
 ,
(2)
,
(2)
и
из фундаментальных функций
 этого уравнения при тех же краевых
условиях, что и выше, для
этого уравнения при тех же краевых
условиях, что и выше, для и
и ,
умножением на
,
умножением на получим фундаментальные функции
получим фундаментальные функции уравнения (1).
уравнения (1).
Введя вместо 𝜆 в качестве нового параметра величину
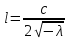
и
вместо
 переменную
переменную
 ,
,
получим дифференциальное уравнение
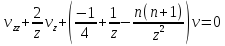 .
.
При
действительном
 ,
т. е. отрицательном
,
т. е. отрицательном условие непрерывности в нулевой точке
и конечности при
условие непрерывности в нулевой точке
и конечности при может быть выполнено лишь для целых
значений
может быть выполнено лишь для целых
значений и что решения даются производными
полиномов Лагерра в следующем виде:
и что решения даются производными
полиномов Лагерра в следующем виде:
 .
.
Следовательно, для первоначального дифференциального уравнения числа
 ,
,
и только эти числа, являются отрицательными собственными значениями, которым принадлежат собственные функции:
 .
.
При
этом
 ,
при заданном целом
,
при заданном целом ,
может пробегать все целые числа от 0 до
,
может пробегать все целые числа от 0 до ,
а
,
а представляет каждый раз
представляет каждый раз линейно независимых шаровых функций.
Найденный таким путем дискретный спектр
состоит из бесконечного множества
функций. Найденный таким путем дискретный
спектр состоит из бесконечного множества
чисел с точкой сгущения нуль.
линейно независимых шаровых функций.
Найденный таким путем дискретный спектр
состоит из бесконечного множества
функций. Найденный таким путем дискретный
спектр состоит из бесконечного множества
чисел с точкой сгущения нуль.
Далее, утверждаем, что уравнение (1) Шредингера имеет собственным значением всякое положительное число 𝜆, т. е. обладает непрерывным спектром в виде континуума всех неотрицательных чисел.
Для
доказательства подставим в (2) вместо
 функцию
функцию ;
получится дифференциальное уравнение
;
получится дифференциальное уравнение
 .
.
Его
решения
 остаются, таким образом, ограниченными
при всяком положительном𝜆,
а решения
остаются, таким образом, ограниченными
при всяком положительном𝜆,
а решения
 стремятся к нулю при бесконечном
возрастании
стремятся к нулю при бесконечном
возрастании .
Для того, чтобы обнаружить, что всякое
положительное число 𝜆 является
собственным значением, остается лишь
доказать существование при всяком
.
Для того, чтобы обнаружить, что всякое
положительное число 𝜆 является
собственным значением, остается лишь
доказать существование при всяком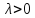 регулярного в нулевой точке решения
регулярного в нулевой точке решения .
Этот факт можно получить из общей теории
линейных дифференциальных уравнений.
Но можно также непосредственно получить
такое решение методом, не раз уже
примененном нами, в виде постоянно
сходящегося степенного ряда, причем
целесообразно предварительно преобразовать
наше дифференциальное уравнение
подстановкой
.
Этот факт можно получить из общей теории
линейных дифференциальных уравнений.
Но можно также непосредственно получить
такое решение методом, не раз уже
примененном нами, в виде постоянно
сходящегося степенного ряда, причем
целесообразно предварительно преобразовать
наше дифференциальное уравнение
подстановкой в такое дифференциальное уравнение для
в такое дифференциальное уравнение для ,
у которого подстановка степенного ряда
приводит к двучленной рекуррентной
формуле.
,
у которого подстановка степенного ряда
приводит к двучленной рекуррентной
формуле.
