Лекция 4. Задачи линейное программирование

План.

4.1. Формы задач линейного программирования.

4.2. Геометрический смысл задачи линейного программирования.

4.1. Формы задач линейного программирования и их эквивалентные преобразования15

На основе примеров задач линейного программирования можно представить три формы задач линейного программирования в зависимости от наличия ограничений разного типа.

1. Стандартная задача линейного программирования

, или

;

. .

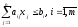Стандартная задача линейного программирования – это задача, в которой система функциональных и прямых ограничений состоит из одних неравенств, переменные являются неотрицательными, а целевая функция может стремиться как к максимуму, так и к минимуму. Причем, в стандартной ЗЛП на максимум все функциональные ограничения имеют форму «меньше или равно». В стандартной ЗЛП на минимум все ограничения имеют форму «больше или равно».

Стандартная задача линейного программирования имеет важное значение ввиду того, что большое число прикладных моделей сводится к этому классу задач линейного программирования.

2. Каноническая задача линейного программирования

;

.

Каноническая задача линейного программирования – это задача, в которой все переменные x_i неотрицательны, система функциональных ограничений представляет собой систему уравнений, а целевая функция стремиться к максимуму.

Основные вычислительные методы (симплекс-метод и его модификации) решения задач линейного программирования разработаны именно для канонической задачи.

3. Общая задача линейного программирования. Необходимо максимизировать (или минимизировать) линейную функцию от n переменных x_1, , x_n вида

при ограничениях

,

,

.

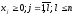Стандартная задача получается как частный случай общей при k = m, l = n; каноническая задача получается как частный случай общей при k = 0, l = n.

Все три задачи эквивалентны в том смысле, что каждую из них можно простыми преобразованиями привести к любой из двух остальных, в том числе задачу на минимум свести к задаче на максимум и наоборот. Поэтому если имеется способ решения одной из этих трех задач, то тем самым может быть решена и любая другая из двух оставшихся.

Эквивалентными называются такие преобразования задач линейного программирования, которые не изменяют оптимального решения задачи. Эквивалентными преобразованиями являются:

- переход от задачи на минимум к задаче на максимум и обратно;

- переход от ограничения в виде неравенства «больше или равно» к ограничению в виде неравенства «меньше или равно»;

- переход от ограничения в виде неравенства к ограничению в виде равенства;

- переход от переменных любого знака к неотрицательным переменным.

Переход от задачи на минимум функции g(X) к задаче на максимум заключается в рассмотрении задачи на максимум функции  g(X):

.

И наоборот переход от задачи на максимум функции f(X) к задаче на минимум заключается в рассмотрении задачи на минимум функции  f(X):

.

Если система ограничений какой-либо задачи включает неравенства разного вида, то необходимо привести исходную ЗЛП к стандартной форме записи, т.е. для ЗЛП на максимум привести все неравенства функциональных ограничений к виду «меньше или равно», а для ЗЛП на минимум – к виду «больше или равно». Для этого используются следующие эквивалентные преобразования:

В задаче на максимум все члены слева и справа от неравенства умножают на (1), а знак неравенства меняют на противоположный:

исходные неравенства: ;

получаемые в результате преобразования неравенства: .

Аналогичным образом поступают и в задаче на минимум:

исходные неравенства: ;

получаемые в результате преобразования неравенства: .

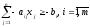Для решения ЗЛП в стандартной форме записи необходимо перейти к эквивалентной ЗЛП в канонической форме записи. Переход от неканонической модели (хотя бы одно ограничение является неравенством) к канонической осуществляется введением в каждое неравенство балансовой переменной x_n+k. При знаке неравенства  балансовая переменная вводится в неравенство со знаком плюс, т.к. левая часть неравенства меньше правой. Если знак неравенства , то балансовая переменная вводится в неравенство со знаком минус, т.к. левая часть неравенства больше правой. При этом для всех балансовых переменных вводится условие неотрицательности. В целевую функцию балансовые переменные не вводятся.

Если сходные неравенства имеют вид , тогда в результате преобразования получают равенстваи неравенства, отражающие условие неотрицательности балансовых переменных.

Если сходные неравенства имеют вид , тогда в результате преобразования получают равенстваи неравенства, отражающие условие неотрицательности балансовых переменных.

Если на переменную x_j общей задачи не накладывается ограничение неотрицательности, то для того, чтобы общую задачу свести к стандартной, необходимо ввести новые переменные ии положить. Таким образом неотрицательное значение – 5 можно заменить двумя положительными значениями 10 и 15: – 5 = 10 – 15.

Задача оптимального распределения ресурсов при планировании выпуска продукции на предприятии, задача на максимум выпуска продукции в заданном ассортименте, задача о смесях являются стандартными задачами линейного программирования, транспортная задача – каноническая задача линейного программирования.