Лекция 14.

1. Расчет на сжатие в полосе бетона стенки балки между наклонными трещинами.

2. Расчет по наклонной трещине на действие поперечной силы. Общее условие прочности.

Расчет на сжатие в полосе бетона стенки балки между наклонными трещинами

На основании экспериментов прочность на действие проверяется из следующего условия:

Q ≤ 0.3·φ_b1·φw₁·R_b·b·h_o

коэффициент, учитывающий влияние прочности бетона, для тяжелого бетона,для легкого

φ_w1=1+5αμ≤1.3

Коэффициент φ_b1 учитывает снижение прочности бетона для случая сжатия с растяжением.

Рис. 116

φ_w1 – учитывает влияние поперечной арматуры.

Рис. 117

S – шаг поперечной арматуры

A_sw – площадь поперечной арматуры

b – ширина элемента

Если условие не выполняется, то необходимо изменить размеры элемента.

Расчет сечения по наклонной трещине на действие поперечной силы

φ_b3=0,6

Прочность обеспечивается бетоном и поперечная арматура не требуется по расчету.

Если условие не выполняется, то необходимо рассчитывать поперечную арматуру.

φ_b3 – коэффициент условия работы бетона по наклонному сечению.

Q_b^(min)=0,6 R_bt b h_o – минимальная несущая способность для прямоугольного сечения.

Q_b^(min)= φ_b3(1+ φ_f+ φ_n)R_b b h_o

Рис. 118

φ_f – учитывает работу свесов сжатой полки

φ_n – учитывает влияние продольной силы

при этом принимается

В любом случае принимается .

Общие условия прочности по наклонному сечению

Чтобы получить условия прочности по наклонному сечению рассмотрим уравнения равновесия в III стадии.

Рис. 119

(.)d – точка приложения равнодействующей сжатой зоны.

Q_b, N_b – вертикальная и горизонтальная составляющие равнодействующей сжатой зоны.

с – величина проекции наклонной трещины.

A_s, A_sw, A_s ^inc – соответственно площадь поперечного сечения продольной, поперечной, наклонной арматуры.

R_s, R_sw – соответственно расчетные сопротивления продольной и поперечной (наклонной) арматуры.

M, Q – внешние расчетные усилия

S – шаг поперечной арматуры

Θ – угол наклона наклонной арматуры

z_s, z_sw, z_s ^inc – расстояния от точки Д до соответственно, продольной, поперечной и наклонной арматуры.

ΣM_(d) = 0 – сумма всех моментов относительно точки (d) равна нулю:

M=M_s+M_sw+M_s,^inc (1)

M_s=A_s·R_s·z_s

_n

M_s,w= Σ Asw·R_sw·z_{sw i}

ⁱ⁼¹

n - количество поперечных плоскостей

M_s^inc= Σ A_s^incR_sw z_s ^inc

Σ Y=0 – сумма проекций всех сил на ось Y равна нулю:

Q=Q_b+Q_sw+Q_s^inc (2)

Q_b – прочность бетона на срез

Q_b = φ_b2(1+ φ_f+ φ_n)·R_bt·b·h_o^²/c

Тяжелый бетон φ_b2=2

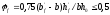
Q_sw = Σ A_sw·R_sw

Q_sw^inc= Σ A_s^inc·R_sw·sinθ

Если выполняется ряд конструктивных требований, то условие (1) можно не рассматривать. В практических расчетах чаще пользуются в основном уравнением (2).

Лекция 15.

1. Расчет хомутов.

2. Расчет на действие изгибающего момента по наклонной трещине

3. Конструктивные требования.

Расчет поперечной арматуры

Наклонная арматура ставится в тех случаях, когда прочность элемента поперечной арматурой не обеспечивается. Рассмотрим, когда Ainc=0.

Рассмотрим условие (2).

со – величина проекции наклонной трещины, на которой работают стержни.

Рис. 120

Сосредоточенные усилия заменим эквивалентными распределенными усилиями q_sw.

Условие (2) будет иметь вид для произвольного значения величины с

(2) при A_s^inc=0

(3)

Найдем такое значение с, при котором несущая способность будет минимальной

(4)

Подставим выражение (4) в условие (3):

(5)

q - учитывают в тех случаях, когда она действует постоянно как длительно действующая нагрузка.

В большинстве случаев .

Из выражения (5):

(6)

Выражение (4) можно получить, если принять

Формула (2) примет вид

Исследования показывают, что ,

Мin армирование поперечными стержнями назначается из условия min прочности по бетону.

–минимальная несущая способность

В общем случае несущую способность Q

Q_м≤ B/c + c_o q_sw проверяют по формуле.

Нормы требуют, чтобы Q_b^min ≤ Q_b – несущая способность на срез

c = c_max

c_max ≤ φ_b2 h_o/ φ_b3

c_max ≤ l/4

Рис. 121

Рис. 122

c_max ≤ a – расстояние до первой сосредоточенной силы.

Чтобы исключить разрушение бетона между смежными плоскостями поперечных стержней S ограничивается.

c = S_max

1)

2)

Рис. 123

4. S должен удовлетворять конструктивным требованиям.

h ≤ 450 h > 450

S ≤ 150 S ≤ 500

S ≤ h/2 S ≤ h/3

Эти требования распространяются на приопорные участки длиной l/4

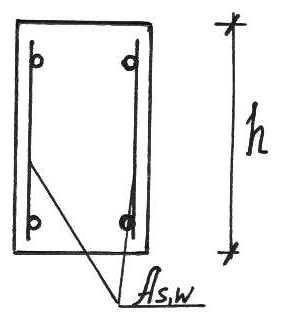
Рис. 124

На среднем участке S<=500, S<=3h/4.

Из 3-х значений S выбирают наименьшее и его окончательно принимают.

Это значение обычно кратно 5 см.

Расчет на поперечную силу выполняют после завершения расчета по нормативному сечению, когда продольная арматура As известна и известно количество стержней и диаметр.

Диаметр поперечной арматуры назначается из условия сварки с продольной.