2.1. Методы интегрирования некоторых классов дифференциальных уравнений, допускающих понижение порядка

Не существует общих приемов, позволяющих проинтегрировать произвольное дифференциальное уравнение высшего порядка. Однако в некоторых случаях порядок дифференциального уравнения может быть понижен и его решение может быть сведено к последовательному интегрированию нескольких дифференциальных уравнений первого порядка. Остановимся на этих случаях.

I.Решение уравнения вида сводится ккратному интегрированию. Общее решение такого уравнения имеет вид

.

Пример. Найти решение уравнения , удовлетворяющее условиям

(2.3)

Решение. Последовательно интегрируя исходное уравнение, будем иметь

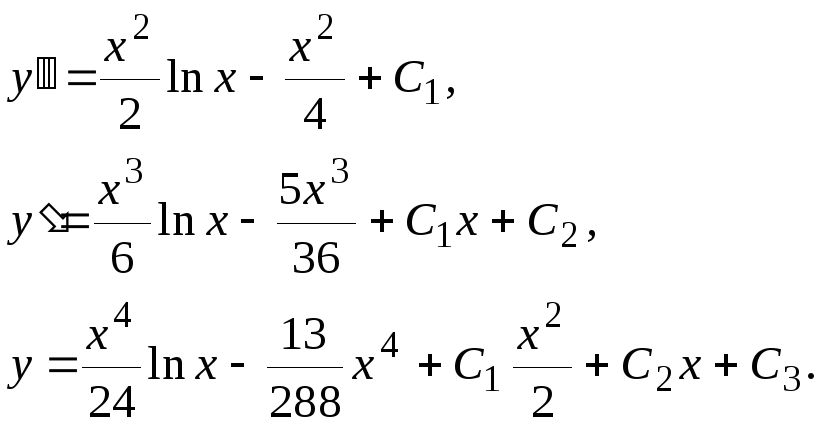
Значения постоянных найдем из условий (2.3). Для отысканияполучим систему уравнений

Итак, искомое решение имеет вид

II.Уравнение не содержит иего производных до порядкавключительно, то есть имеет вид .

Для понижения порядка уравнения применяется подстановка . После применения этой подстановки уравнение приобретает вид. Если удается найти общее решение последнего уравнения, то после-кратного интегрирования получим общее решение исходного уравнения.

Пример. Проинтегрировать уравнение .

Решение. Уравнение не содержит и его производных до третьего порядка включительно. Поэтому его порядок понижается путем введения заменыОтносительно новой переменной уравнение имеет вид

Последовательно интегрируя последнее равенство четыре раза, получим

III.Уравнение не содержит явно переменной , то есть имеет вид. В этом случае порядок уравнения понижается путем замены. Последовательно получим

.

Приходим к уравнению -го порядка

Если удалось найти общее решение последнего уравнения, то для отысканиябудем иметь уравнение с разделяющимися переменными

.

Пример. Проинтегрировать уравнение в области

Решение. Уравнение не содержит явно переменной . Поэтому выполним заменуУравнение примет вид. Разделив обе части этого уравнения на, получим– уравнение Бернулли относительно. Решение этого уравнения будем искать в виде произведения функций. Подставляя в уравнение, будем иметьВ качестве функциивозьмем решение уравненияТогда для отысканияполучим:

Итак,

Найден общий интеграл уравнения.

IY. Уравнение однородное относительно и его производных. Однородным называется уравнение , для которого выполнено

.

Порядок однородного уравнения понижается путем введения новой переменной по правилу . Тогда получим

.

При этом исходное уравнение принимает вид

.

Пусть найдено его решение . Для нахожденияполучаем уравнение с разделяющимися переменными, решение которого имеет вид. Заметим, что решениездесь не потеряно. Оно получается из последней формулы при.

Пример. Проинтегрировать уравнение

Решение. Левая часть уравнения– однородная функция относительно Выполним замену. Тогда уравнение примет вид

Общее решение последнего уравнения (линейного относительно ) имеет видТогдаРешениеполучается при

V. Уравнение имеет вид . Иными словами, левая часть этого уравнения представляет собой полную производную поот некоторой функции. Интегрируя обе части такого уравнения по, получим новое уравнение, порядок которого на единицу меньше, чем у исходного.

Пример. Проинтегрировать уравнение

Решение. Очевидным решением этого уравнения является функция Разделив обе части уравнения на, получим

.

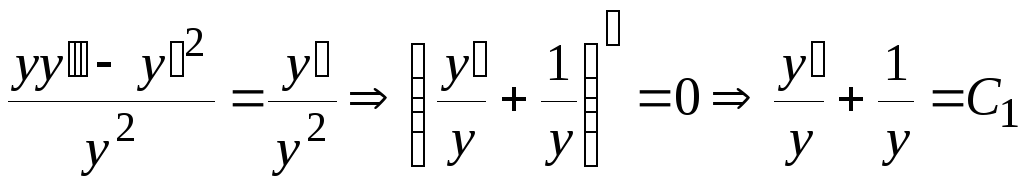При получаемПриполучаем линейное уравнение, общее решение которого имеет вид.