- •Министерство образования и науки Российской Федерации
- •Задание 9.2
- •Задание 9.3
- •Задание 9.4
- •Задание 9.5
- •Задание 9.6
- •Задание 9.7
- •Задание 9.8
- •Задание 9.9
- •Задание 9.10
- •Задание 9.11
- •Задание 9.12
- •Задание 9.13
- •Задание 9.14
- •Задание 9.15
- •Задание 9.16
- •Задание 9.17
- •Задание 9.18
- •Задание 9.19
- •Задание 9.20
- •Задание 9.21
- •Задание 9.22
- •Задание 9.23
- •Задание 9.24
- •Задание 9.26
- •Задание 9.27
- •Задание 9.28
- •Задание 9.29
Задание 9.5
Найдите наименьшее число испытаний Бернулли, необходимое для того, чтобы с вероятностью, не меньшей заданной, можно принять относительную частоту успехов за вероятность успеха в одном испытании с погрешностью, не превышающей заданную.
Варианты 1-10. Провайдер утверждает, что вероятность соединиться с сетью с первого звонка достаточно велика. Сколько нужно произвести экспериментов, чтобы с вероятностью не менее можно было утверждать, что относительная частота соединений с первого звонка отличается от заявленной вероятности не более, чем на ?
-
№
9
0.92
0.07
Определим,
сколько нужно произвести испытаний,
чтобы отклонение относительной частоты
успехов
![]() от вероятностиp
было
меньше e
с
вероятностью, большей или равной ,
т.е. найдем n,
для которого выполняется неравенство
от вероятностиp
было
меньше e
с
вероятностью, большей или равной ,
т.е. найдем n,
для которого выполняется неравенство
![]() .
.
Доказано, что число n обеспечивает выполнение этого неравенства, если оно удовлетворяет соотношению
![]()
где
x
—
решение
уравнения
![]() .
.
Следует
обратить особое внимание на замечательный
факт — искомое
значение n
не зависит от p
и
поэтому формулой
![]() следует пользоваться для оценки
минимально необходимого числа испытаний
при неизвестной вероятности р.
Если
вероятность p
изначально
известна, то необходимое число испытаний
определяется формулой
следует пользоваться для оценки
минимально необходимого числа испытаний
при неизвестной вероятности р.
Если
вероятность p
изначально
известна, то необходимое число испытаний
определяется формулой
![]() .
.
Решение:
![]()
![]()
![]()
![]()
![]()
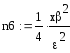
![]()
Искомое значение n= 157.
Задание 9.6
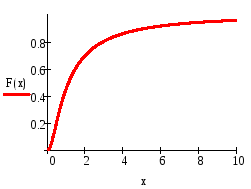
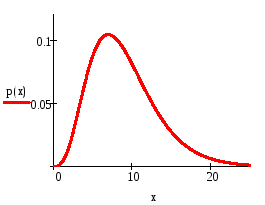
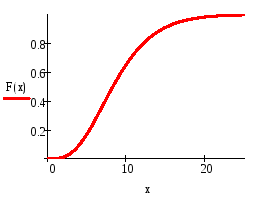
Постройте графики плотности распределения и функции распределения 2 c указанным числом степеней свободы, равным п = 9.
Распределение xи-квадрат (2-распределение). Пусть 1, 2, … n - независимые случайные величины, каждая из которых имеет стандартное нормальное распределение N(0, 1). Составим случайную величину
![]() .
.
Ее распределение называется 2-распределением с n степенями свободы. Для справочных целей приведем здесь выражение плотности распределения этой случайной величины:
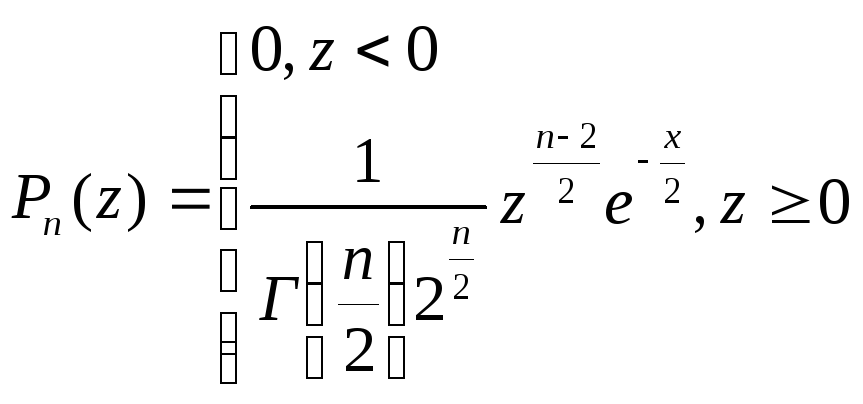 ,
,
где Г(x) — гамма-функция Эйлера:
![]() .
.
Решение:
![]()
![]()
![]()
Задание 9.7
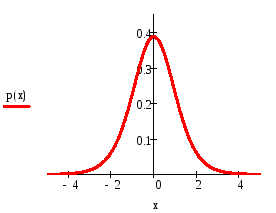
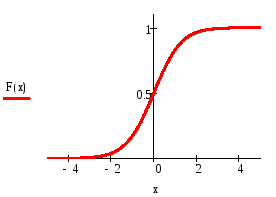
Постройте графики плотности распределения и функции распределения Стьюдента с указанным числом степеней свободы, равным k = №. Здесь № — номер варианта.
.
Распределение
Стьюдента.
Пусть
случайная величина
имеет стандартное нормальное распределение,
а случайная величина
![]() 2-распределение
с n
степенями
свободы. Если
и
2-распределение
с n
степенями
свободы. Если
и
![]() независимы,
то про случайную величину
независимы,
то про случайную величину
![]()
говорят, что она имеет распределение Стьюдента с числом степеней свободы п. Доказано, что плотность вероятности этой случайной величины вычисляется по
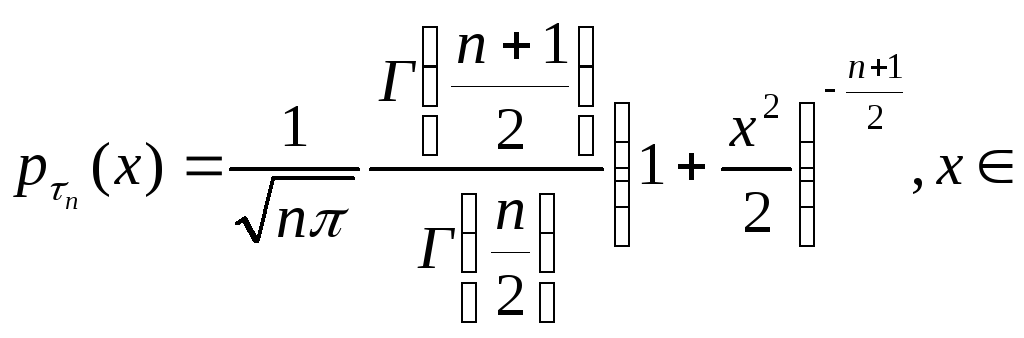 R
R
При больших n распределение Стьюдента практически не отличается от N(0,1).
Решение:
![]()
![]()
![]()
|
N |
п |
т |
|
9 |
6 |
3 |
Задание 9.8
Постройте графики плотности распределения и функции распределения Фишера для указанных значений n и m.
F-распределение
Фишера.
Пусть
случайные величины
![]() и
и
![]() независимы и имеют распределение 2
с n
и m
степенями свободы соответственно. Тогда
случайная величина
независимы и имеют распределение 2
с n
и m
степенями свободы соответственно. Тогда
случайная величина
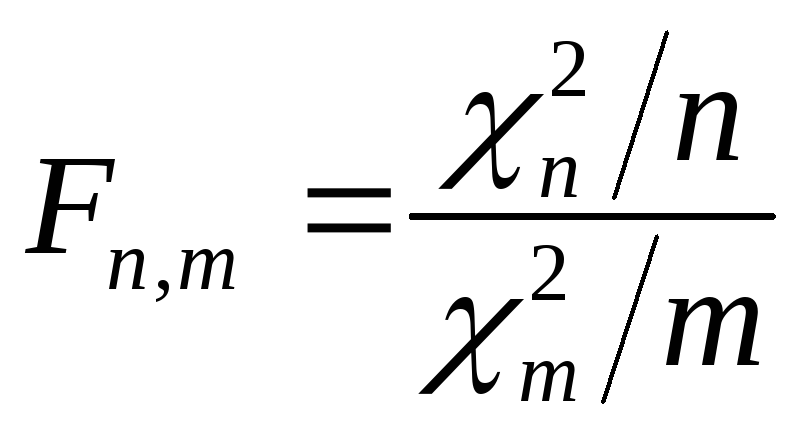 имеетF-распределение
с плотностью вероятности
имеетF-распределение
с плотностью вероятности
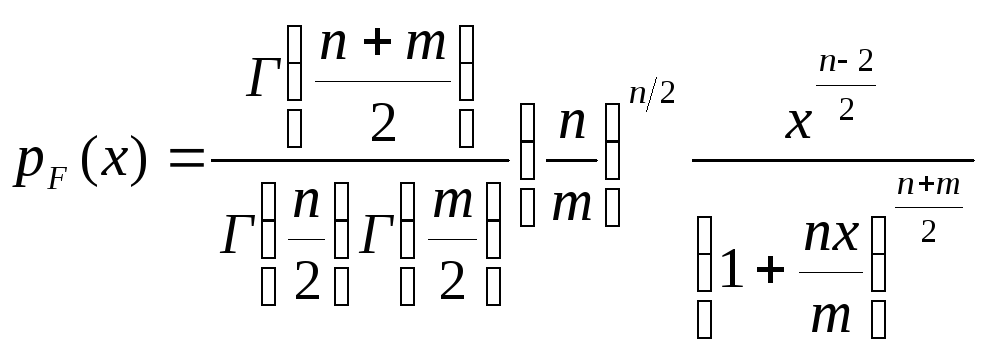 ,
x
> 0.
,
x
> 0.
Решение:
![]()
![]()
![]()
![]()