
- •Аннотация
- •Содержание
- •1 Исходные данных
- •I II III I II III
- •2 Основные положения метода начальных параметров
- •3 Задача о равновесии прямого стержня постоянного сечения
- •4 Построение стержневого конечного элемента с использованием аналитических решений уравнений состояния
- •5 Выполнение индивидуального задания
- •9 Выводы
- •Список использованных источников
4 Построение стержневого конечного элемента с использованием аналитических решений уравнений состояния
Рассмотрим выражения для вектора состояния в произвольной точке стержня:
![]() .
(21)
.
(21)
Представим
вектор состояния (3) в виде объединения
двух блоков, один из которых характеризует
кинематические параметры стержня
![]() ,
а другой – силовые параметры
,
а другой – силовые параметры![]() .
.
![]() (21)
(21)
Аналогично запишем для вектора нагрузки:
![]() ,
(22)
,
(22)
где
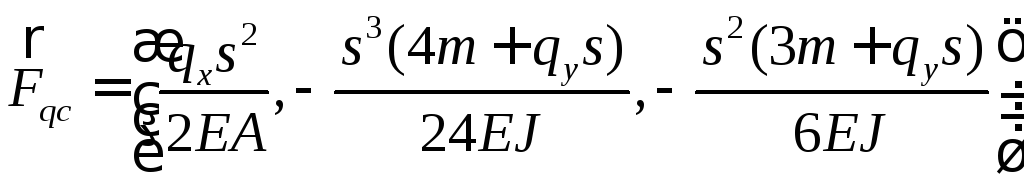 ,
,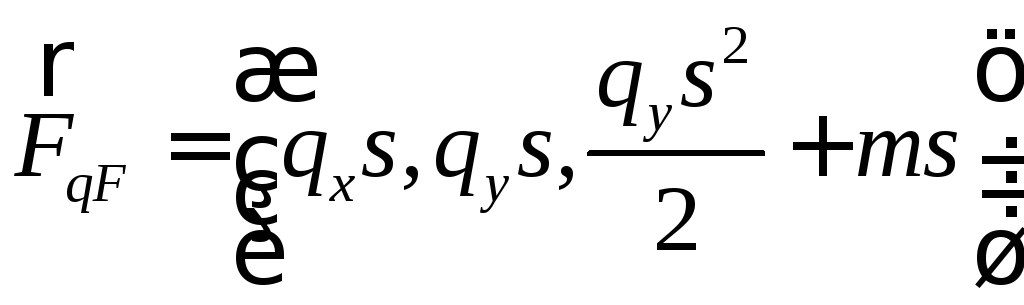 .
.
Матрицу влияния разобьем на четыре блока:
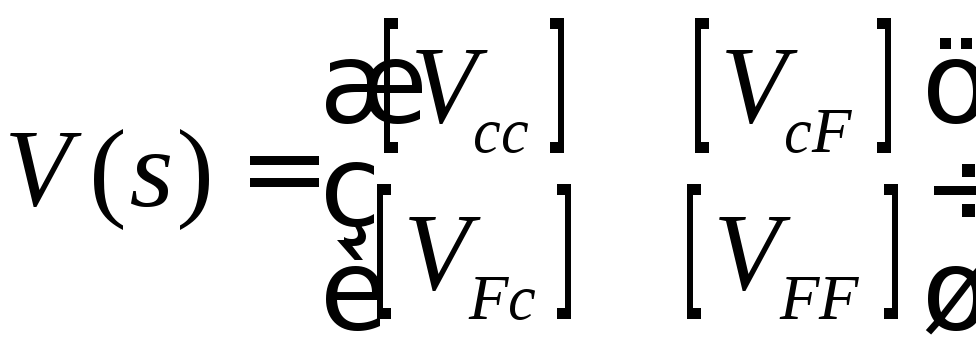 ,
(23)
,
(23)
где
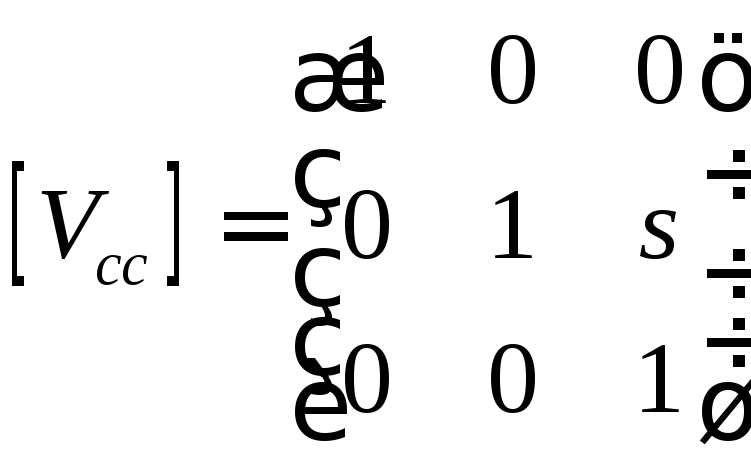 ,
,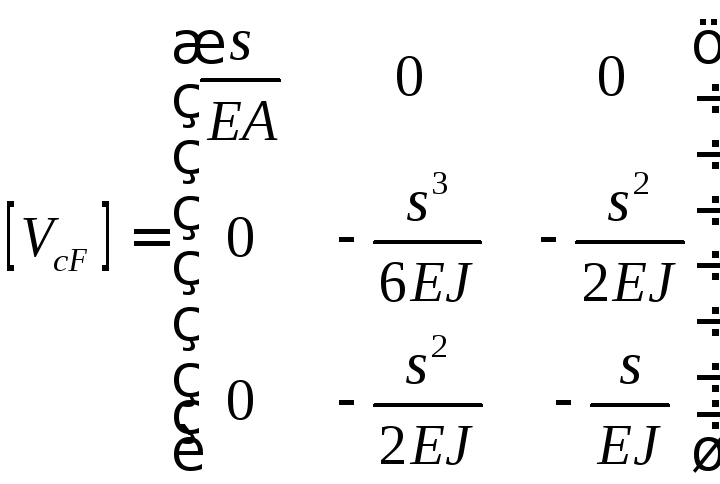 ,
,
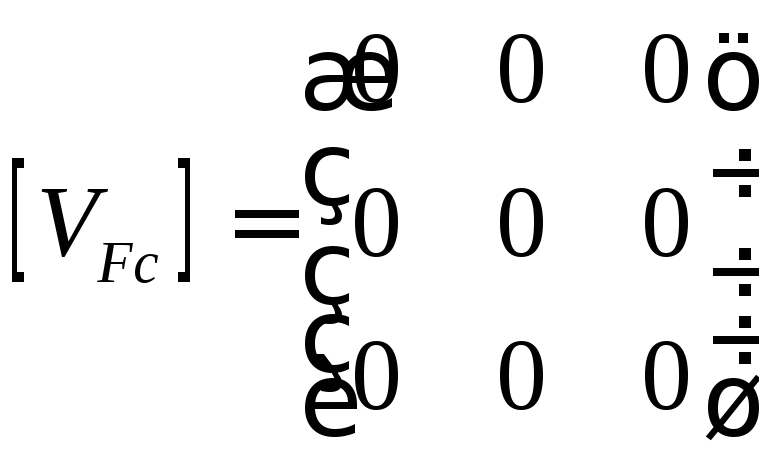 ,
,
 .
.
Запишем
уравнение (21) для конца стержня
![]() :
:
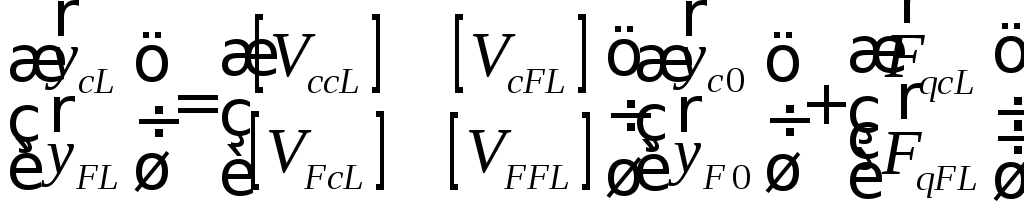 .
(24)
.
(24)
Выразим
из (24) вектор начальных силовых параметров
![]() :
:
![]() .
(25)
.
(25)
Получим выражение для состояния стержня в любой точке через параметры начала и конца, для чего подставим (25) обратно в (21). Сгруппировав подобные слагаемые, получим уравнение, связывающее состояние стержня в любой его точке с кинематическими параметрами его начала и конца:
![]() ,
(26)
,
(26)
где
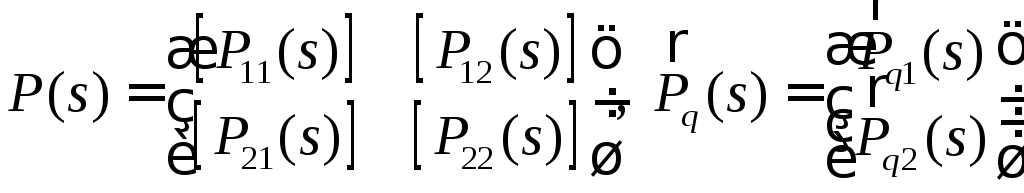 – соответственно блочная матрица и
вектор, устроенные аналогично (22) и (23).
– соответственно блочная матрица и
вектор, устроенные аналогично (22) и (23).
Компоненты
матрицы связи
![]() и вектора
и вектора![]() имеют следующий вид:
имеют следующий вид:
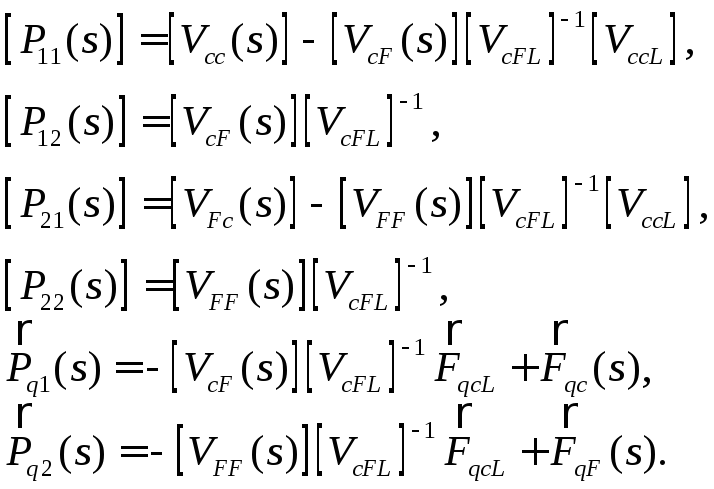 .
(27)
.
(27)
Чтобы
найти узловые перемещения, воспользуемся
методом вырезания узлов. Для этого
запишем состояние в начале и в конце
стержня. Из уравнений, определяющих
силовые параметры, получаются условия
равновесия стержня:
![]() .
Учтем при этом, что матрица влияния
.
Учтем при этом, что матрица влияния![]() – нормированная матрица фундаментальных
решений, то есть выполняется условие
– нормированная матрица фундаментальных
решений, то есть выполняется условие![]() – единичная матрица.
– единичная матрица.
 (28)
(28)
Запишем уравнения (28) в матричном виде:
![]() ,
(29)
,
(29)
где
компоненты блоков матрицы
![]() и вектора
и вектора![]() имеют следующий вид:
имеют следующий вид:
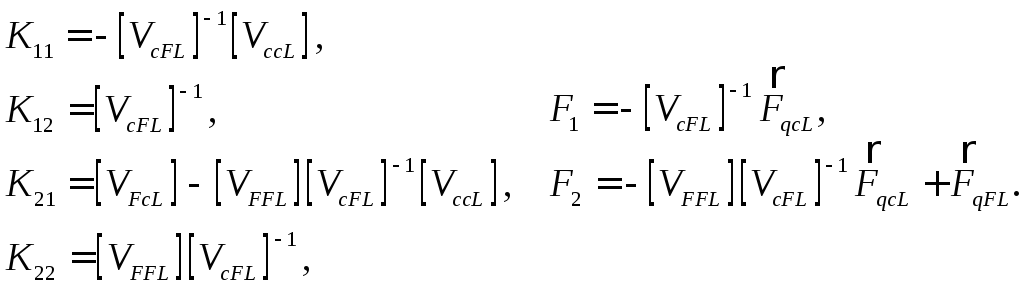 (30)
(30)
Уравнение
(29), связывающее узловые перемещения
стержня с распределенной нагрузкой,
действующей на него, по определению
является разрешающим уравнением метода
конечных элементов. Тогда
![]() – матрица жесткости стержневого
конечного элемента.
– матрица жесткости стержневого
конечного элемента.
5 Выполнение индивидуального задания

Рисунок 2 - Схема конструкции 1 Конструкция представляет собой прямой стержень с шарниром на левом конце и свободным краем – на правом конце. Из последнего следует, что схема является статически определимой. Значит, производить расчет удобнее методом начальных параметров. Стержень нагружен различными силовыми факторами: сосредоточенной силой P и равномерной нагрузкой q. Поэтому разобьем стержень следующим образом:

Рисунок 3 - Выделение узлов. Конструкция 1
Запишем систему уравнений метода начальных параметров, из которой будем искать кинематические и силовые параметры стержня:
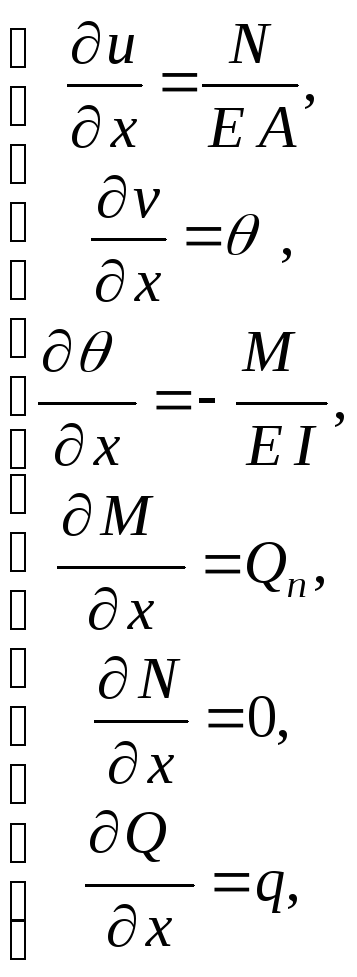
где
![]() – изгибающий момент,Q
– поперечная сила, q
– распределенная поперечная нагрузка,
u
– линейное перемещение вдоль нормали
стержня,
– изгибающий момент,Q
– поперечная сила, q
– распределенная поперечная нагрузка,
u
– линейное перемещение вдоль нормали
стержня,
![]() – угловое перемещение вокруг бинормали,E
– модуль Юнга, I
–
момент инерции относительно оси,
перпендикулярной плоскости изгибающего
момента. х – координата вдоль оси
стержня.
1) матрица модели А, полученная
из системы диф уравнений от
– угловое перемещение вокруг бинормали,E
– модуль Юнга, I
–
момент инерции относительно оси,
перпендикулярной плоскости изгибающего
момента. х – координата вдоль оси
стержня.
1) матрица модели А, полученная
из системы диф уравнений от
(u/v/teta/N/Q/M)
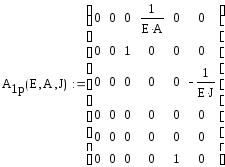 2)
матрица влияния получена преобразованием
Лапласа
2)
матрица влияния получена преобразованием
Лапласа
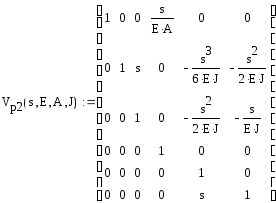
аналитическое решение МНП позволяет найти вектор нагрузки:
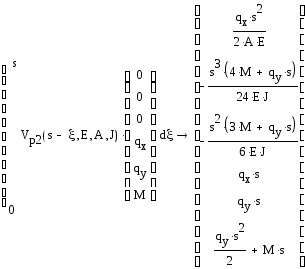

Разобьем на блоки:
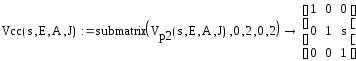

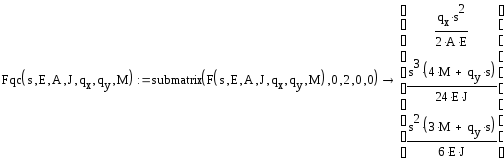

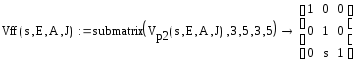
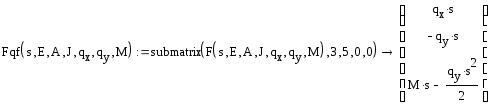
Эти формулы исключают элементы, отвечающие за силовые нагрузки из матрицы влияния:
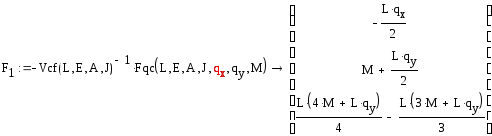
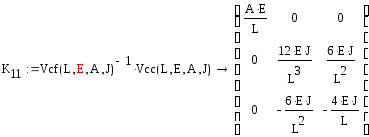
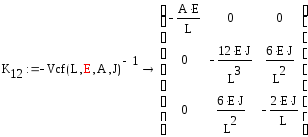
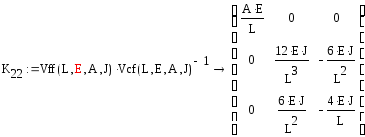
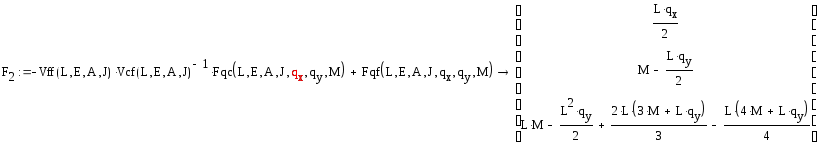

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
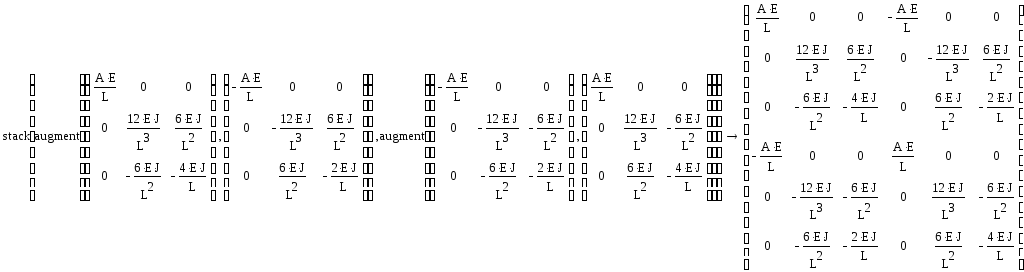
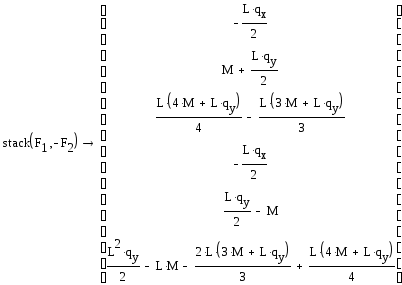
Матрица
жесткости элемента связывает перемещения
и угол поворота начала и конца и вектор
нагрузки:

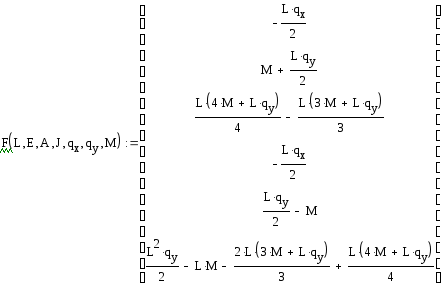
Теперь необходимо получить силы:
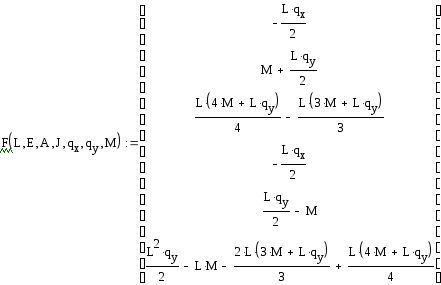
Выполнение расчета для схемы 1.
Исходные
данные:
![]()
![]()
![]()
![]()
![]()
Площадь
сечения:
![]()
Модуль
упругости (Юнга):
![]()
![]()
Массив данных: Условия закрепления: 0 - есть закрепление по данному перемещению, 1 - свободное перемещение.
![]()
![]()
![]()
Связи: ‘’0 - закрепление, 1 – свободно’’
Структура: 1- перемещение по x для первого узла,
2- перемещение по y для первого узла,
3- угол поворота для первого узла
4- перемещение по x для второго узла
5- перемещение по y для второго узла
6-
угол поворота для второго узла
 Процедура
вычисляющая длину стержня:
Процедура
вычисляющая длину стержня:

{ne номер элемента, для которого считается длина
Len - длина элемента}
![]()
![]()
![]()
Процедура составляющая глобальную матрицу жесткости:

{ne - номер элемента, для которого считается длина Ans - в конце выводится глобальная матрица жесткости}



вектор перемещений
U - это вектор глобальных перемещений, в котором перемещения всех узлов записаны по порядку. Чтобы интерпретировать полученные результаты, необходимо получить векторы узловых перемещений для каждого из элементов:
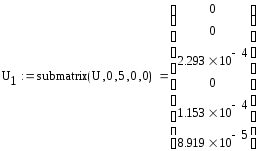


![]()
![]()
![]()
![]()
![]()
![]()
![]()
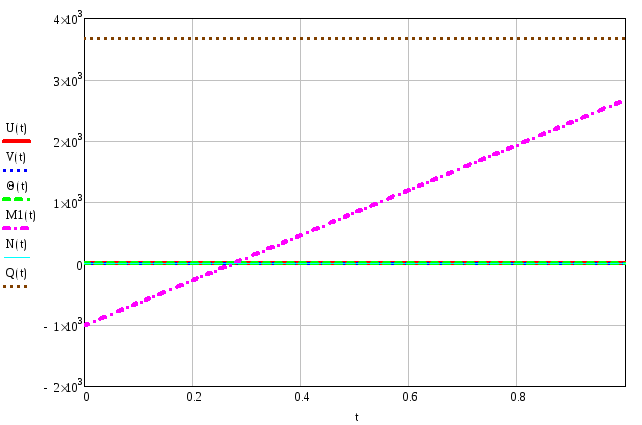
Эпюры внутренних силовых и кинематических факторов для первого элемента:
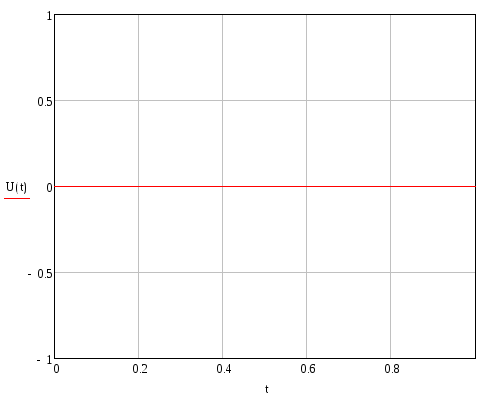
Продольное перемещение
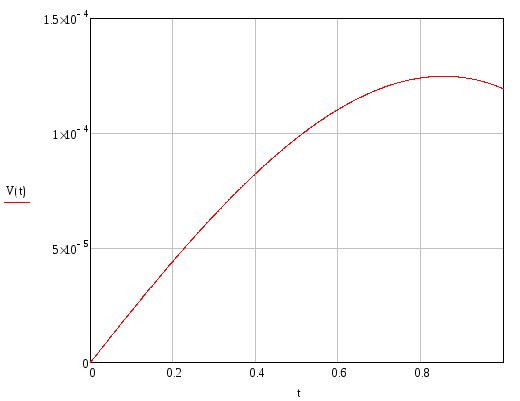

Угол поворота
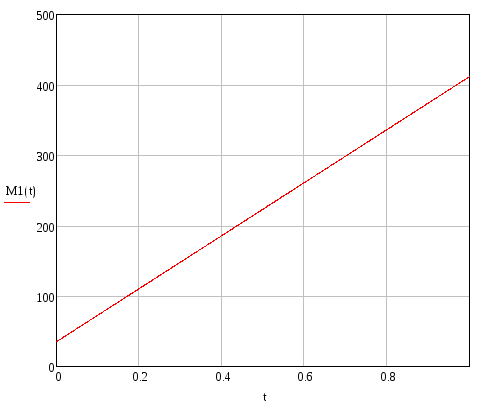
Изгибающий момент
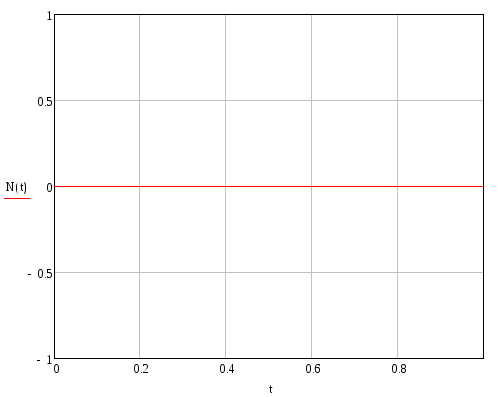
Продольная сила
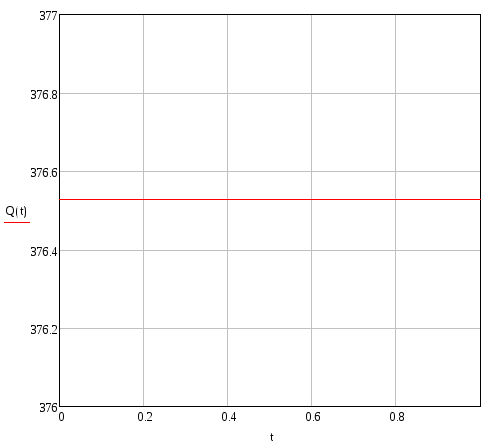
Поперечна сила

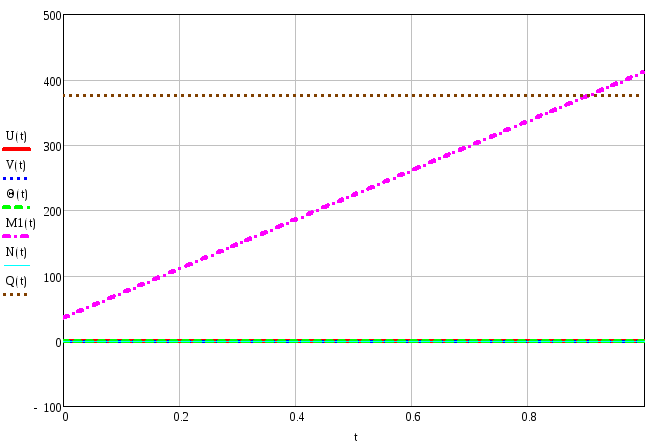
Эпюры внутренних силовых и кинематических факторов для второго элемента:
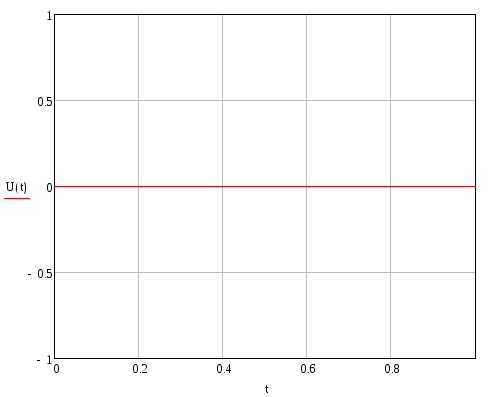
Продольное перемещение
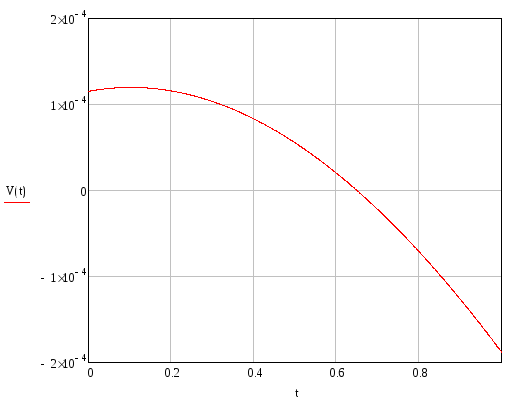
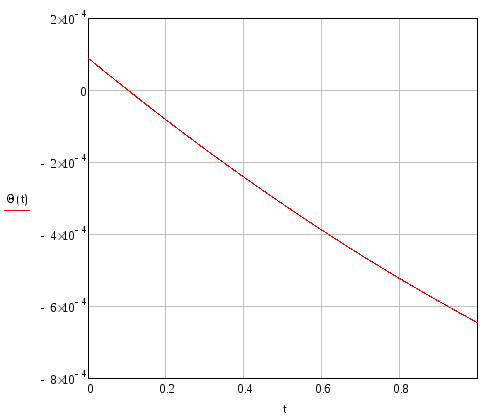
Угол поворота
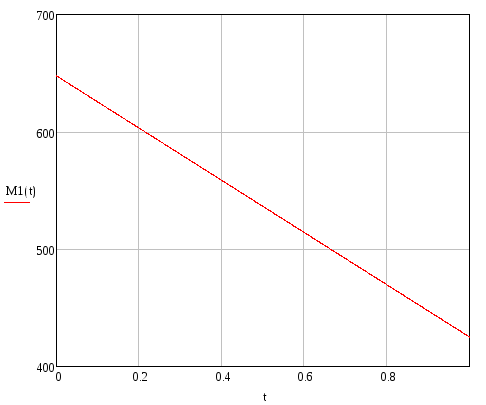
Изгибающий момент
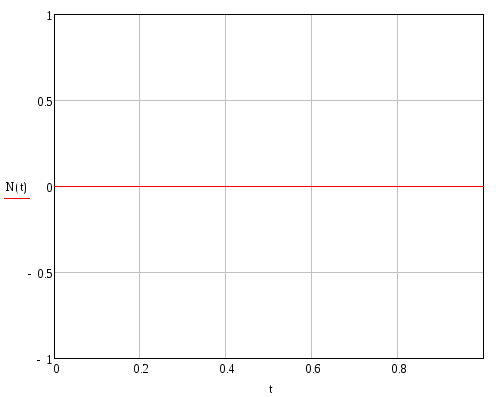
Продольная сила
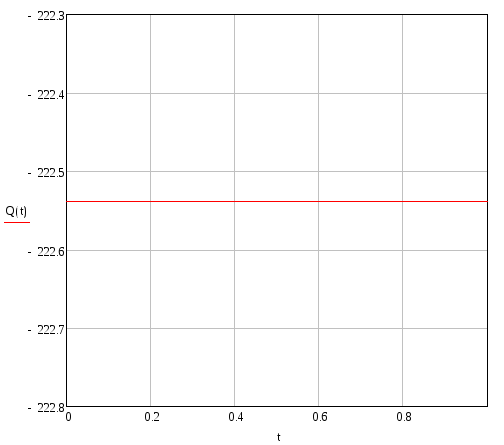
Поперечна сила
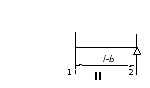
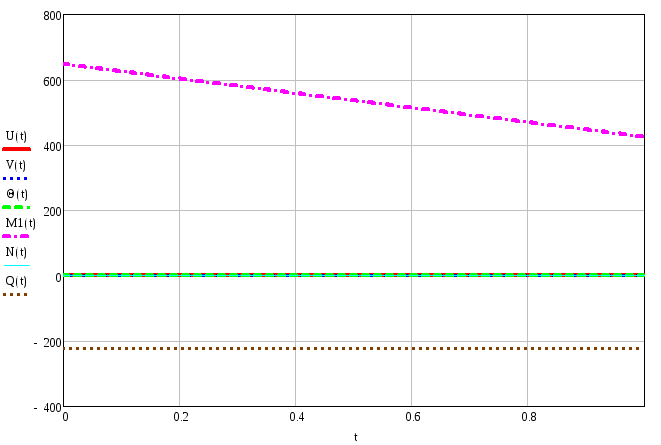
Эпюры внутренних силовых и кинематических факторов для третьго элемента:
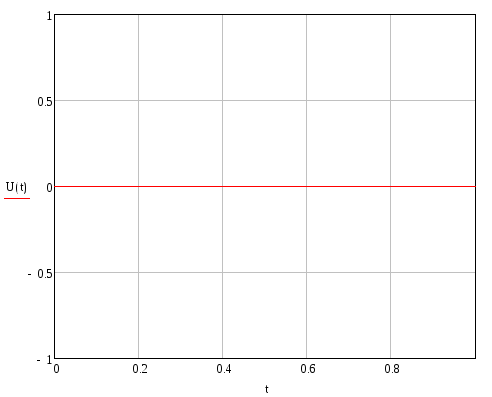
Продольное перемещение
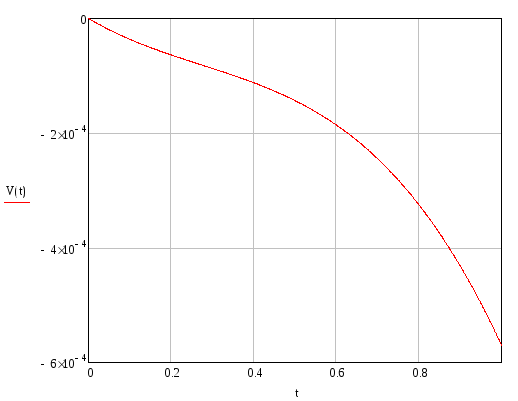
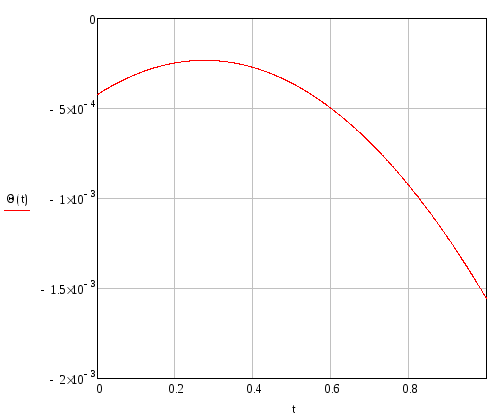
Угол поворота
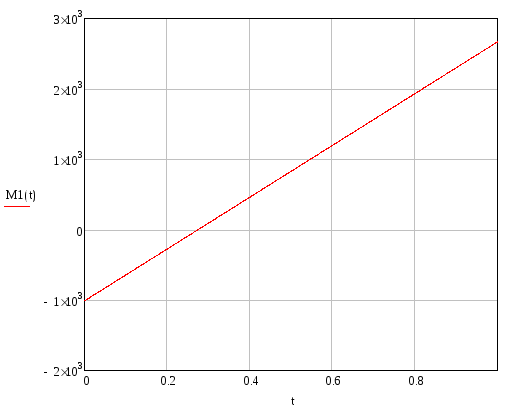
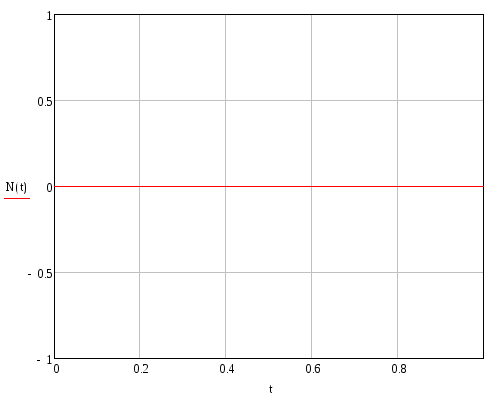
Продольная сила
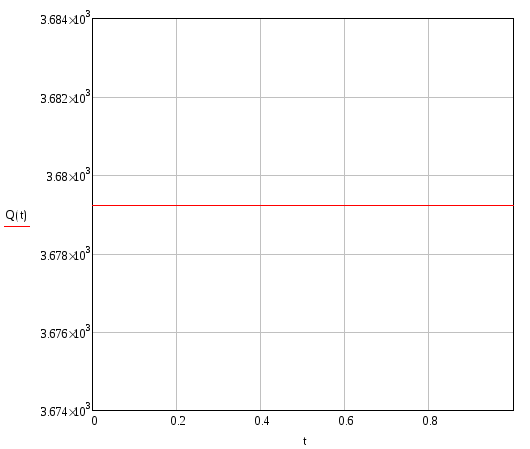
Поперечна сила

![]()
![]()
![]()
![]()
![]() можно сделать о том, что конструкция
выдержит заданную нагрузку.
можно сделать о том, что конструкция
выдержит заданную нагрузку.
Схема 2
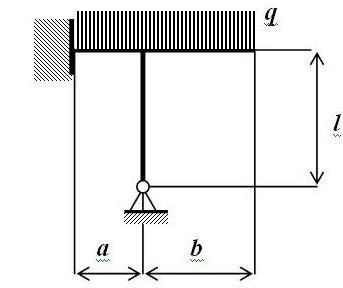
Рисунок 4 - Схема конструкции 2
Данная схема представляет собой стержневую систему с жесткой заделкой и неподвижной шарнирной опорой. Схема является статически неопределимой. Все эти факторы говорят о неудобстве использования МНП в том виде, который использовался при решении задания №1. Однако, можно совместить МНП с методом конечных элементов, которым и воспользуемся при решении задачи. Как было сказано выше, будем использовать метод, совмещающий МНП и МКЭ.
Отметим,
что вектор состояния содержит в себе
кинематические и силовые параметры.
Тогда его можно разбить на 2 части:
![]() .
.
где
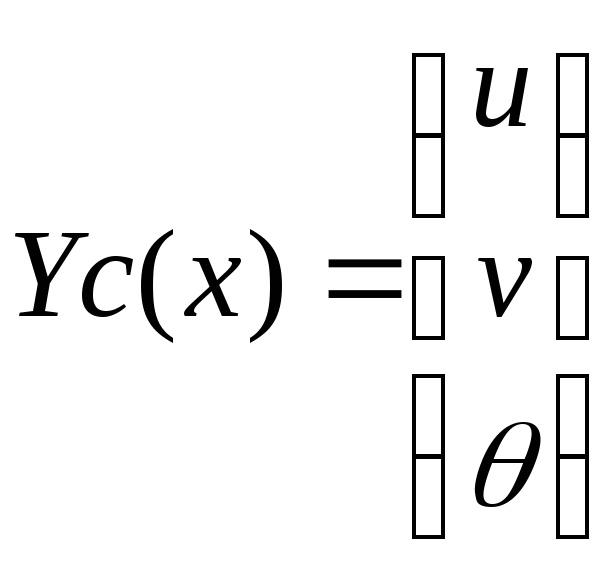 и
и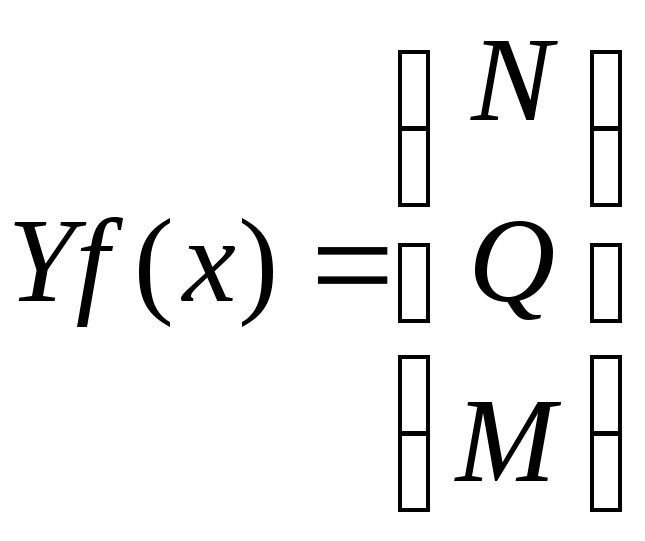 .
.
Тогда естественно будет разбиение матрицы влияния на 4 блока:
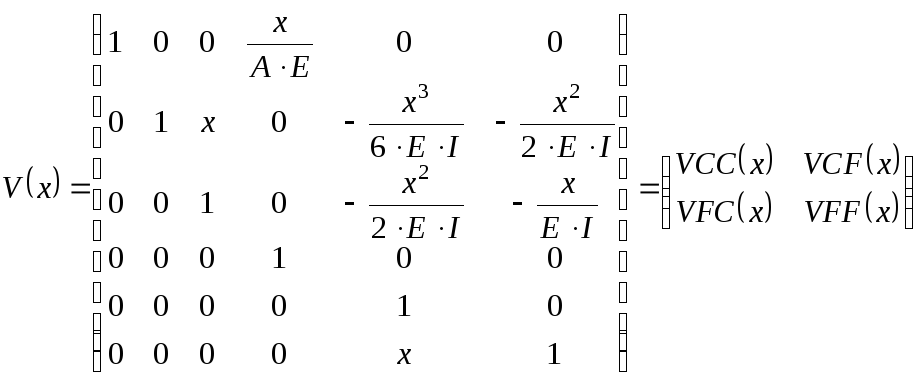
где каждый блок несет вполне понятную информацию:
VCC – влияние кинематических параметров на кинематические
VCF – влияние силовых параметров на кинематические
VFC – влияние кинематических параметров на силовые
VFF – влияние силовых параметров на силовые
Влияние распределенных нагрузок также разобьем на 2 части:

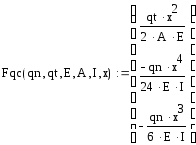
- влияние нагрузок на кинематические параметры
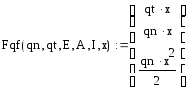
- влияние нагрузок на силовые параметры
Тогда векторы перемещений и силовых факторов можно записать в виде:
![]()
Запишем полученное первое уравнение для x=L и выразим из него начальные силовые параметры:
![]()
Подставим выражение во второе уравнение:
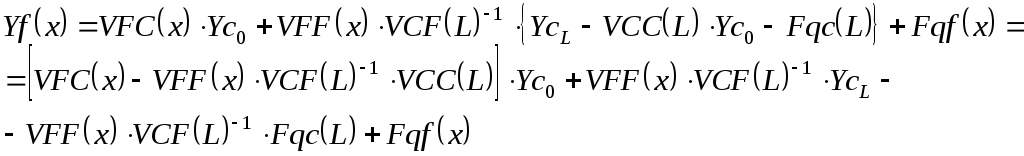 Таким
образом, мы выразили силовые параметры
через перемещения узлов, что напоминает
КЭ-подход.
Таким
образом, мы выразили силовые параметры
через перемещения узлов, что напоминает
КЭ-подход.
Перед последующими преобразованиями, отметим, что матрица VFC является нулевой.
Составим вектор силовых параметров в узлах:
![]() ,
где
,
где
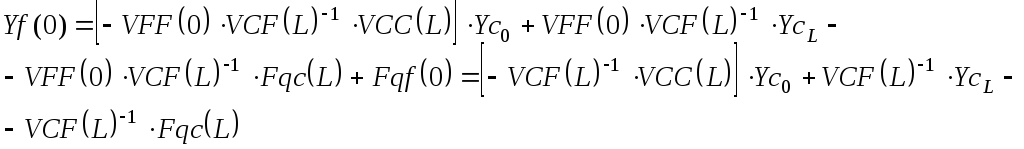
![]()
Введем также вектор узловых перемещений:
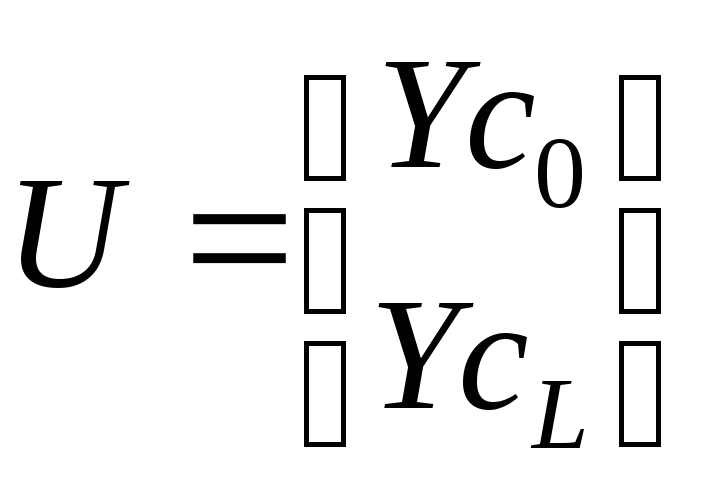
Тогда можно записать следующее уравнение:
![]() ,
где K
– аналог матрицы жесткости, а R
– влияние распределенных нагрузок.
Приведем их вид:
,
где K
– аналог матрицы жесткости, а R
– влияние распределенных нагрузок.
Приведем их вид:
Определение матрицы жесткости:
![]()
![]()
![]()
![]()
![]()
![]()
![]()

- матрица жесткости в локальных координатах
Исходные данные берем из первой задачи: Эпюры внутренних силовых и кинематических факторов для первого элемента:
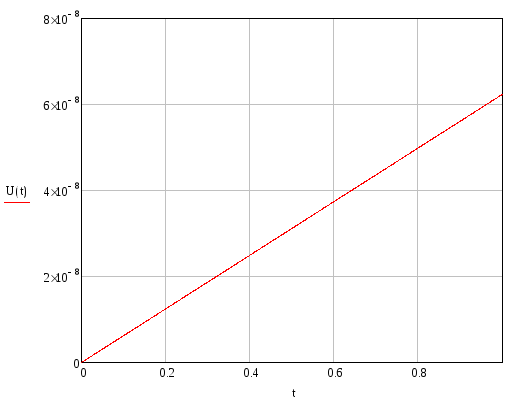
Продольное перемещение
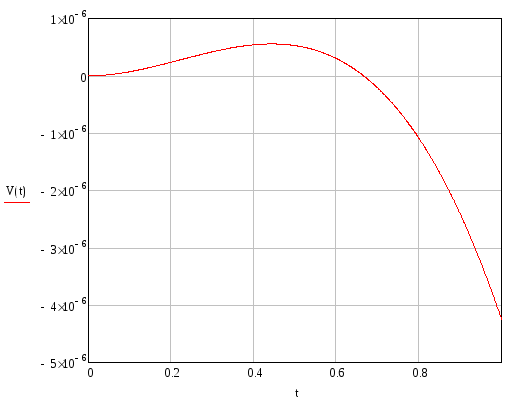
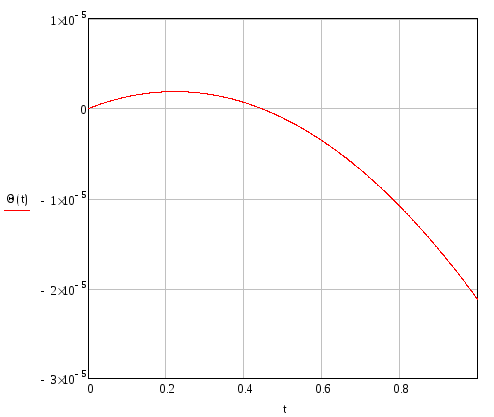
Угол поворота


Продольная сила
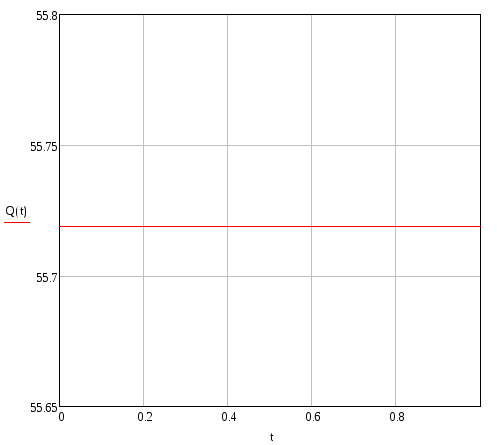
Поперечна сила

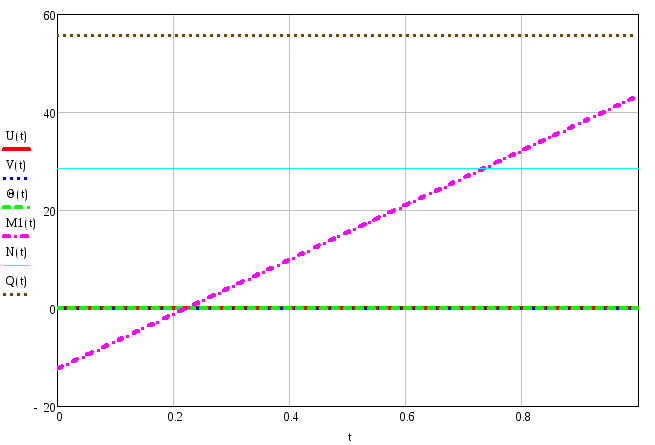
Эпюры внутренних силовых и кинематических факторов для второго элемента:
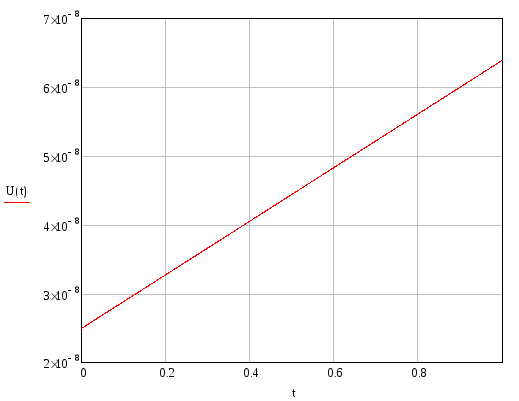
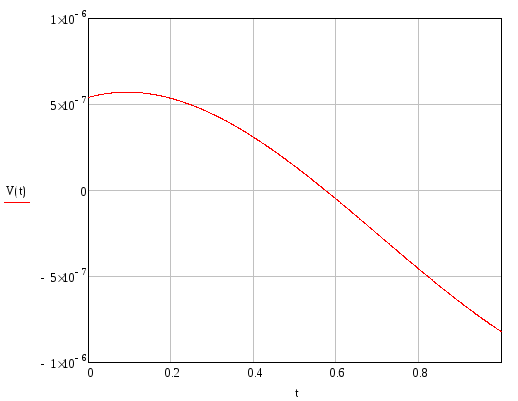
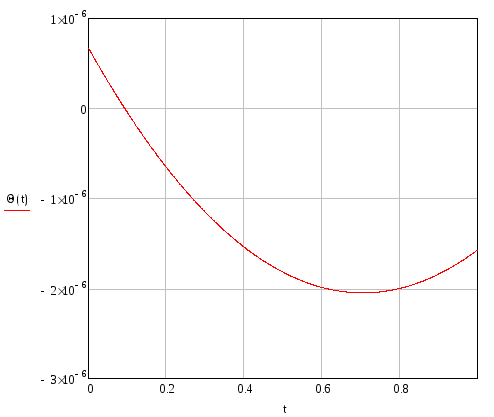
Угол поворота
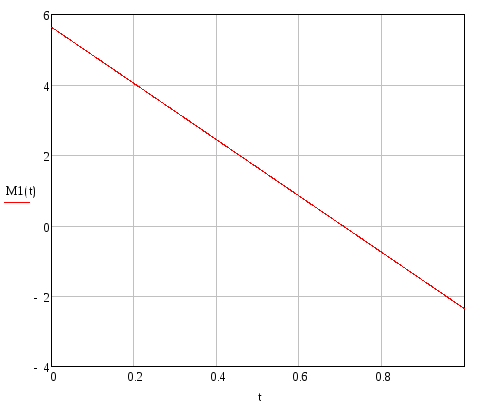
Изгибающий момент
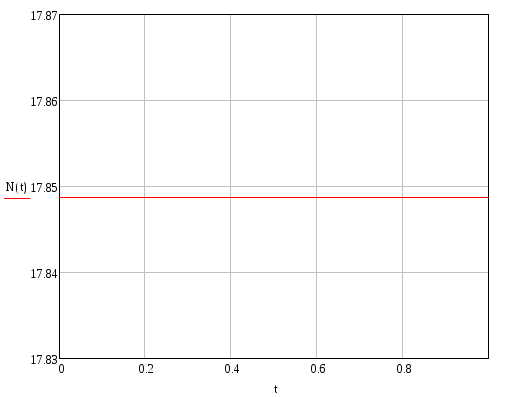

Поперечна сила

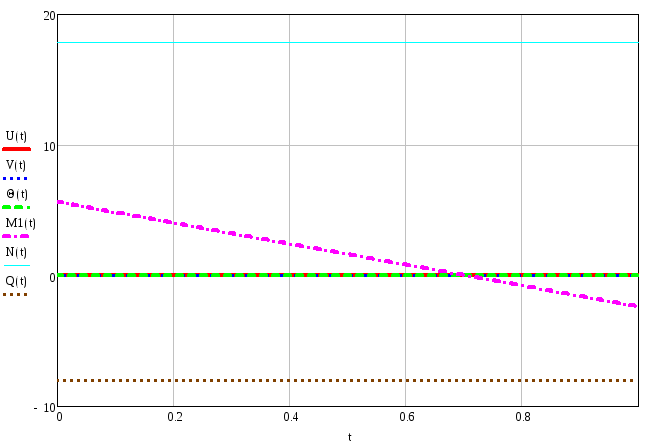
Эпюры внутренних силовых и кинематических факторов для третьего элемента:
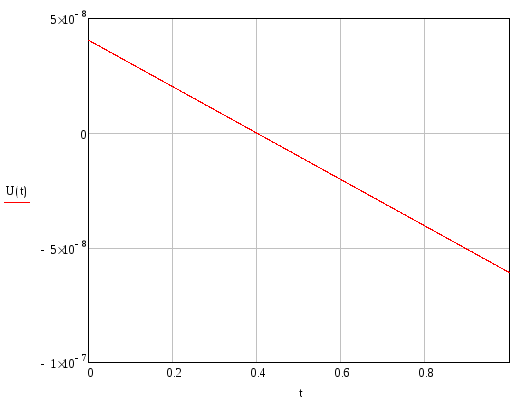

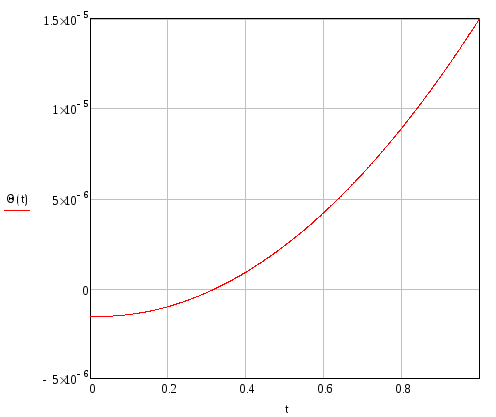
Угол поворота
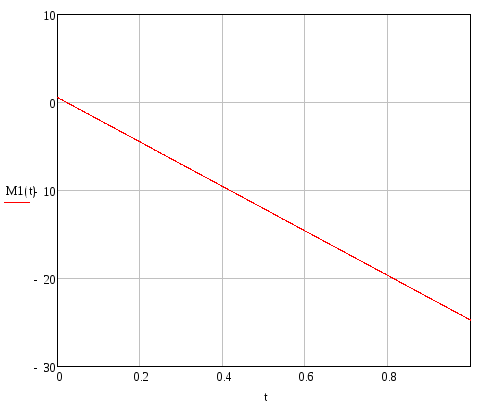
Изгибающий момент

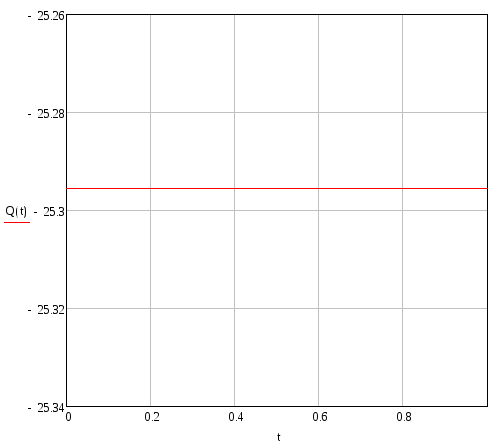
Поперечна сила

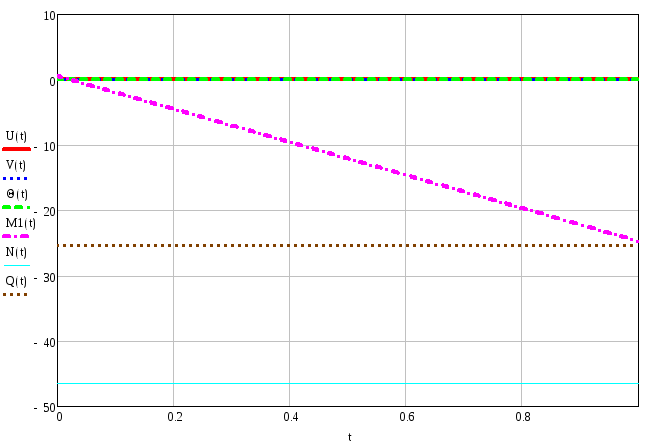
![]()
![]()
![]()
![]()
![]() можно сделать о том, что конструкция
выдержит заданную нагрузку.
можно сделать о том, что конструкция
выдержит заданную нагрузку.
