matmodeli_Borisova_laba_1
.docМИНОБРНАУКИ Российской Федерации
ГОУ ВПО «Тульский государственный университет»
Кафедра ПМиИ
Лабораторная работа №1
на тему: «Обтекание сферы потоком несжимаемой идеальной жидкости».
Выполнил: ст.гр.520281 Логвинова А.Л.
Принял: Ларин Н.В.
Тула 2012
-
ЦЕЛЬ РАБОТЫ
Приобретение навыков математического моделирования процесса обтекания сферы потоком несжимаемой идеальной жидкости и аналитического решения этой задачи.
-
ЗАДАНИЕ
-
Построить модель процесса обтекания сферы потоком жидкости.
-
Провести подробное аналитическое решение задачи.
-
Определить компоненты вектора скорости частиц жидкости.
-
Найти распределение скоростей частиц жидкости на поверхности сферы.
-
С помощью интеграла Бернулли определить давление на поверхности сферы.
-
Рассчитать зависимость давления на поверхности сферы от полярного угла .
-
Рассчитать зависимость величин Vr и V от угла при r = 1,2a; 5a; 10a.
-
Рассчитать зависимости Vr и V от r в диапазоне изменения r от a до 10a при любых значениях .
-
ВЫПОЛНЕНИЕ
-
Математическая модель процесса обтекания сферы потоком жидкости
Движение несжимаемой идеальной жидкости описывается системой уравнений гидродинамики, состоящей из уравнения Эйлера
![]() (1)
(1)
и
уравнения неразрывности, которое в
случае несжимаемости жидкости (плотность
![]() )
имеет вид
)
имеет вид
![]() , (2)
, (2)
где
![]() -
скорость жидкости;
-
скорость жидкости;
![]() - давление;
- давление;
![]() - массовая сила, отнесенная к единице
массы.
- массовая сила, отнесенная к единице
массы.
Используя формулу векторного анализа
![]()
и рассматривая стационарное безвихревое движение жидкости при отсутствии массовых сил, из уравнения (1) получим
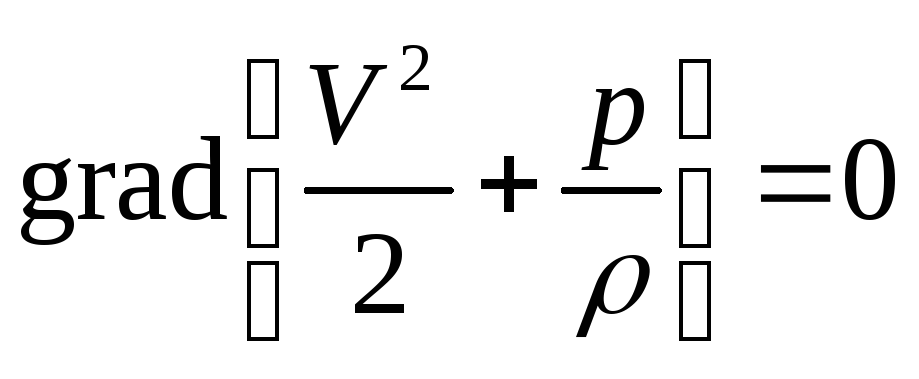
следовательно,
![]() , (3)
, (3)
где С – константа, имеющая одно и то же значение во всех точках движущейся жидкости. Равенство (3) называется интегралом Бернулли.
Рассмотрим задачу
об обтекании неподвижной абсолютно
твердой сферы стационарным потоком
идеальной жидкости. Пусть незавихренный
поток несжимаемой идеальной жидкости,
двигаясь поступательно со скоростью
![]() ,
обтекает на своем пути твердую сферу
радиуса а. Определим поле скоростей
возмущенного движения жидкости.
,
обтекает на своем пути твердую сферу
радиуса а. Определим поле скоростей
возмущенного движения жидкости.
Считая движение
безвихревым
![]() ,
введем в рассмотрение потенциал скоростей
,
введем в рассмотрение потенциал скоростей
![]() .
При этом скорость частиц жидкости будет
определяться формулой
.
При этом скорость частиц жидкости будет
определяться формулой
![]() .
.
Для решения задачи
введем систему сферических координат
![]() с началом в центре сферы и направим ось
z в сторону, противоположную
движению потока (рис.1).
с началом в центре сферы и направим ось
z в сторону, противоположную
движению потока (рис.1).
Из уравнения
неразрывности следует, что потенциал
скоростей
![]() для несжимаемой жидкости должен
удовлетворять всюду вне сферы уравнению
Лапласа
для несжимаемой жидкости должен
удовлетворять всюду вне сферы уравнению
Лапласа
![]() (4)
(4)
Граничное условие
на поверхности сферы состоит в равенстве
нулю нормальной составляющей скорости
![]() :
:
![]() (5)
(5)
Кроме того, потенциал
![]() в бесконечности должен удовлетворять
условию
в бесконечности должен удовлетворять
условию
![]() . (6)
. (6)
Потенциал
![]() представим в виде суммы двух слагаемых
представим в виде суммы двух слагаемых
![]() , (7)
, (7)
где
![]() - потенциал скоростей однородного
потока;
- потенциал скоростей однородного
потока;
![]() -
потенциал скоростей возмущенного
потока.
-
потенциал скоростей возмущенного
потока.
Тогда из выражений (3), (5) и (6) получаем
![]() (8)
(8)
![]() ; (9)
; (9)
![]() . (10)
. (10)
Таким образом, задача состоит в нахождении решения уравнения (8), удовлетворяющего граничному условию (9) и условию на бесконечности (10).
-
Аналитическое решение задачи
В сферической системе координат
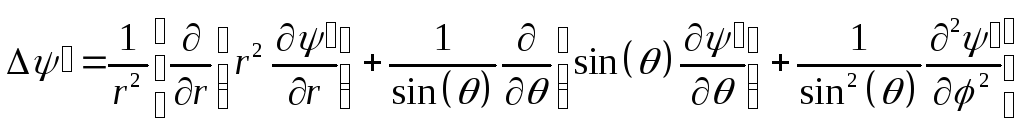 .
.
Так как рассматриваем
осесимметричную задачу, то функция
![]() не зависит от координаты
не зависит от координаты
![]() .
Поэтому уравнение (8) принимает вид
.
Поэтому уравнение (8) принимает вид
![]() . (11)
. (11)
Будем решать уравнение (11) методом разделения переменных. Для этого полагаем
![]() . (12)
. (12)
Подставляя (12) в (11), получим
![]() .
.
Так
как левая часть последнего равенства
не зависит от
![]() ,
а правая от r, то можем
записать
,
а правая от r, то можем
записать
![]() .
.
где
![]() - постоянная разделения, которую считаем
неотрицательной.
- постоянная разделения, которую считаем
неотрицательной.
Положим
![]() ,
где n – целое число. Тогда
для первого уравнения будем иметь
,
где n – целое число. Тогда
для первого уравнения будем иметь
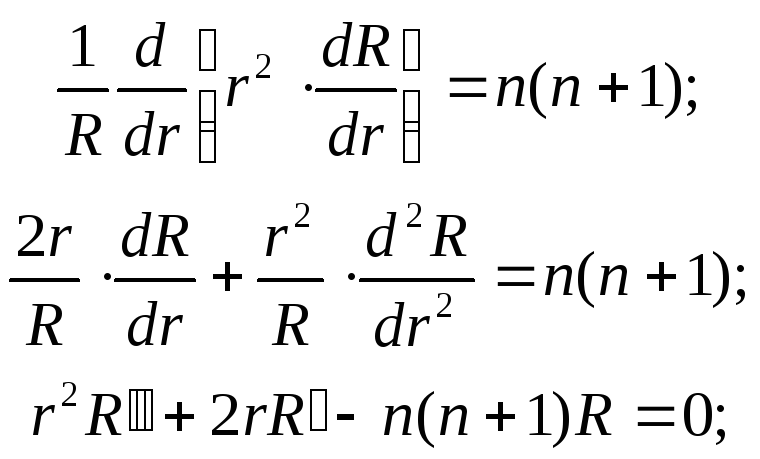
Положим
![]() ,
получим:
,
получим:
![]()
Подставим в исходное уравнение, получим:
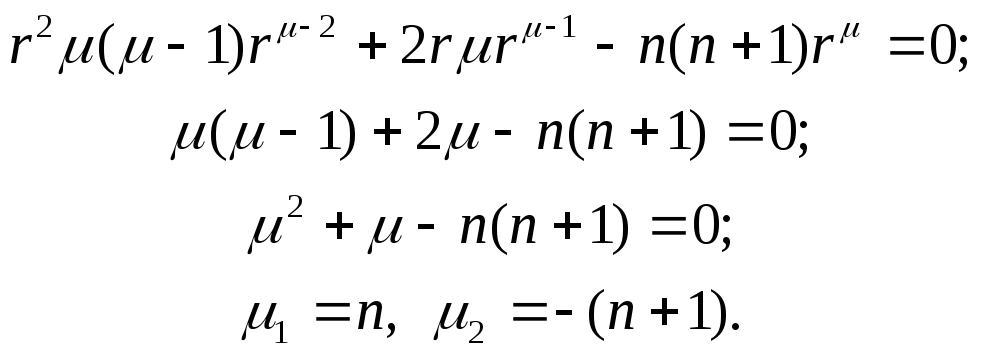
Окончательно получаем решение:
![]()
где
![]() - постоянные.
- постоянные.
Решим второе уравнение:
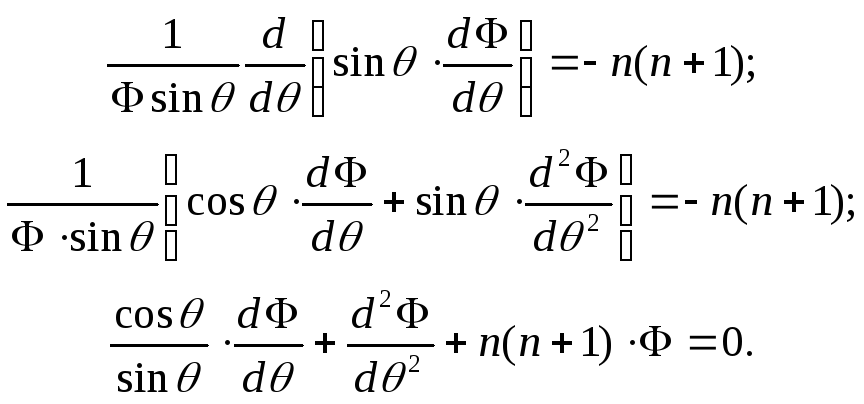
Обозначим
![]() ,
тогда уравнение примет вид
,
тогда уравнение примет вид
![]() (14)
(14)
Положим
![]() ,
тогда
,
тогда
![]() .
Отсюда следует:
.
Отсюда следует:
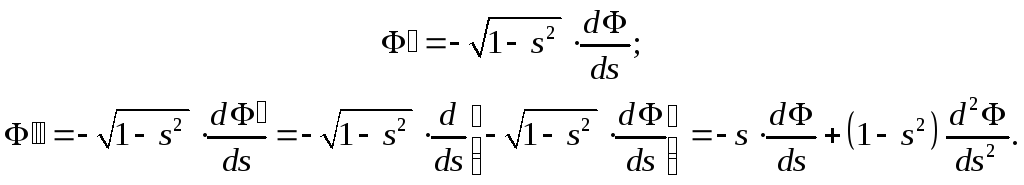
Подставим полученные выражения в (14):
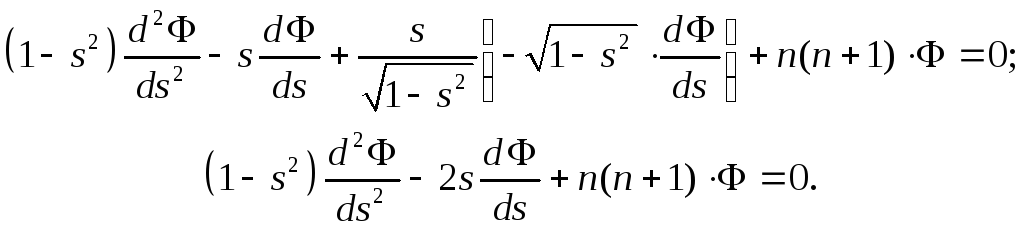
Получили дифференциальное уравнение Лежандра.
Окончательно получаем решение:
![]()
где
![]() - постоянные;
- постоянные;
![]() - полином Лежандра
порядка n.
- полином Лежандра
порядка n.
Для выполнения
условия (10) необходимо положить
![]() .
Таким образом,
.
Таким образом,
![]() ,
,
где
![]() - некоторая постоянная.
- некоторая постоянная.
Будем искать
потенциал
![]() в виде ряда
в виде ряда
![]()
Подставляя этот ряд в граничное условие (9), получаем
![]() .
.
Учитывая,
что
![]() ,
находим
,
находим
![]() .
.
Таким образом,
![]() .
.
На основании формулы (7) окончательно получаем решение задачи
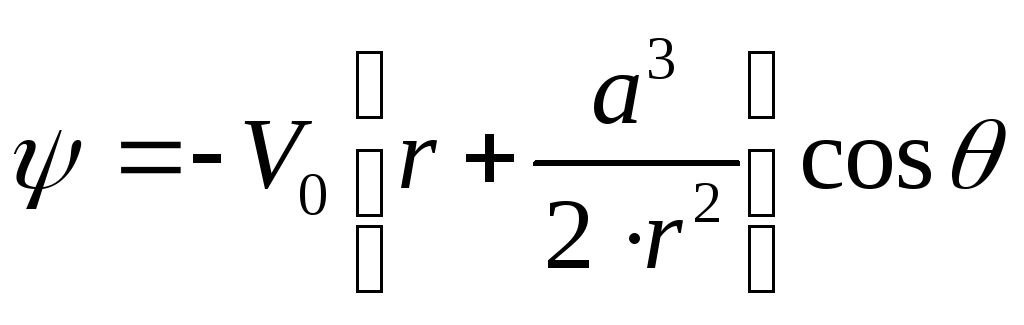 .
.
-
Определение компонент вектора скорости частиц жидкости
Определив потенциал
скоростей
![]() ,
можем найти компоненты вектора скорости
частиц жидкости по формулам
,
можем найти компоненты вектора скорости
частиц жидкости по формулам
![]() .
.
Окончательно получаем:
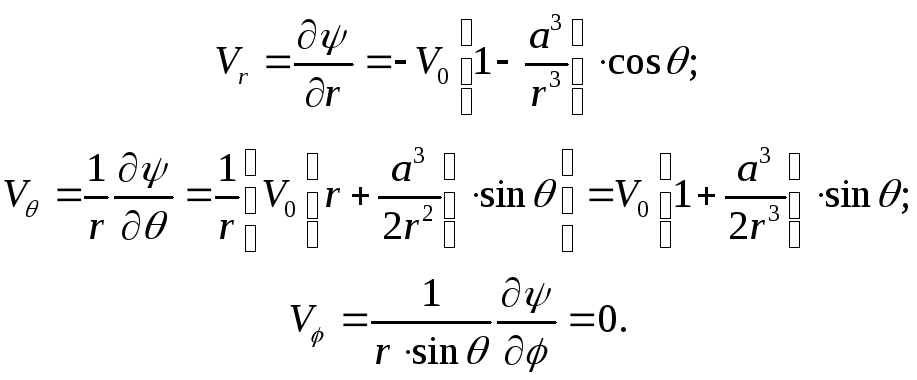
-
Нахождение распределения скоростей частиц жидкости на поверхности сферы
На поверхности сферы, т. е. при r = a, компоненты скорости равны:
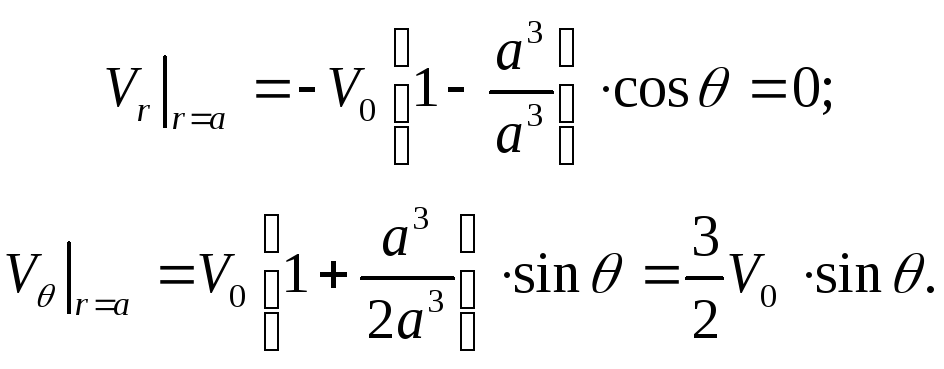
Тогда модуль скорости частиц жидкости на поверхности сферы равен:
![]()
-
Определение давления на поверхности сферы.
Для определения давления воспользуемся интегралом Бернулли:
![]() ,
,
где
![]() .
.
На поверхности сферы будем иметь
![]() .
.
Отсюда видно, что распределение давления относительно плоскости XOY, перпендикулярной к направлению потока, симметрично. Тогда ясно, что давления, приложенные к поверхности сферы, взаимно уравновешиваются. Это, так называемый, парадокс Даламбера. Он объясняется тем, что в действительности безотрывное безвихревое обтекание сферы не имеет места. С поверхности сферы срываются вихри, которые видоизменяют как картину течения, так и распределение давления на поверхности сферы.
Пункты 6,7 и 8 представлены на графиках:
> restart;
> psi:=(r,theta)->-V0*(r+(a^3)/(2*r^2))*cos(theta):
> V0:=1;
> a:=3;
> q:=-V0*(r+(a^3)/(2*r^2))*cos(theta):
> Vr:=diff(q,r);
> Vtheta:=diff(q,theta)/(r);
> r:=3;
> V:=(Vr^2+Vtheta^2)^(1/2):
> ro:=1000;
> C:=3500;
> p:=(theta)->C-9/8*ro*V^2*(sin(theta))^2;
![]()
![]()
![]()
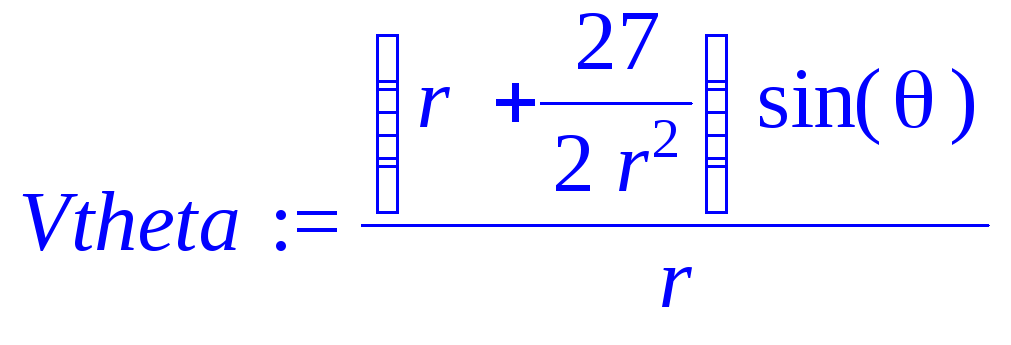
![]()
![]()
![]()
![]()
> Vthetag:=(re,theta)->((r+27/2/r^2)*sin(theta))/r;
> Vrg:=(re,theta)->-(1-27/re^3)*cos(theta);
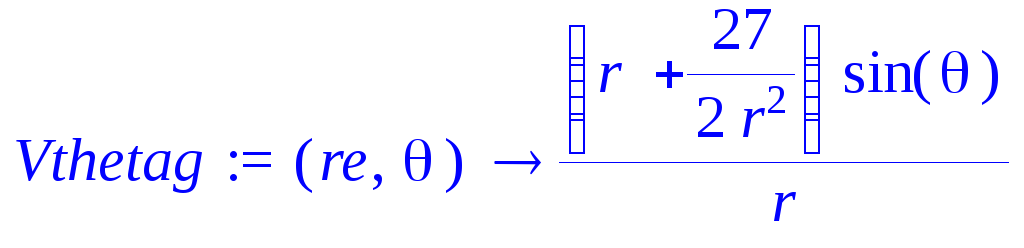
![]()
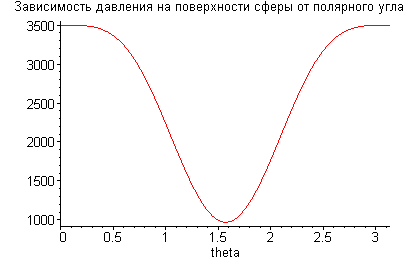
> plot(p(theta),theta=0..Pi,title= "Зависимость давления на поверхности сферы от полярного угла");
> r:=1.2*a:
> plot([Vrg(r,theta),Vthetag(r,theta)],theta=0..Pi,color=[red,blue],title= "Зависимость величин Vr и Vtheta от полярного угла. r=1.2a");

> r:=5*a:
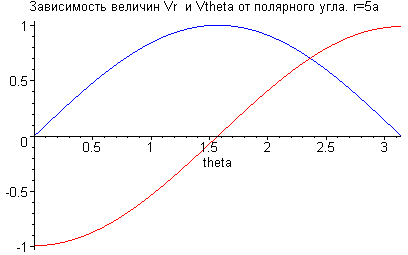
> plot([Vr,Vtheta],theta=0..Pi,color=[red,blue],title= "Зависимость величин Vr и Vtheta от полярного угла. r=5a");
> r:=10*a:
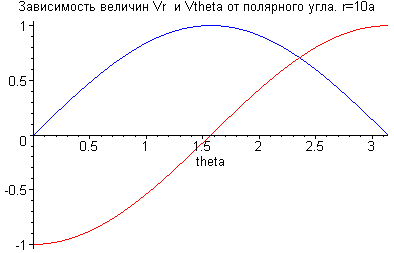
> plot([Vr,Vtheta],theta=0..Pi,color=[red,blue],title= "Зависимость величин Vr и Vtheta от полярного угла. r=10a");
> plot3d(Vrg(w,theta),w=a..10*a,theta=0..Pi,color=[black,blue],title= "Зависимость величины Vr от r при любых значениях Theta");
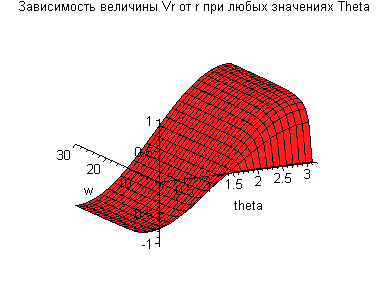
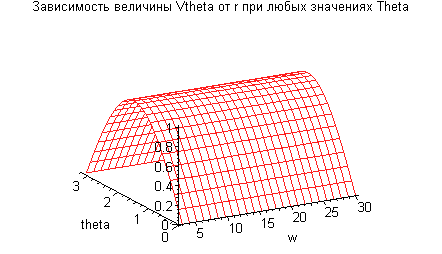
> plot3d(Vthetag(w,theta),w=a..10*a,theta=0..Pi,color=[red,blue],title= "Зависимость величины Vtheta от r при любых значениях Theta");