7.2. Определение зависимости между моделируемыми показателями и определяющими их факторами

Основные подходы к решению этой проблемы базируются на методах содержательного анализа закономерностей, подкрепляемых при необходимости статистическими методами. Характерной особенностью эконометрического исследования является то, что на начальной стадии исследования априорно не известны вид функциональной зависимости и точный состав включаемых в нее факторов. Поэтому, прежде чем подойти к определению типа зависимости между переменными необходимо выбрать показатели, адекватно отражающие сущность исследуемых явлений и обосновать наличие факта взаимосвязи между явлениями.

На этапе содержательного анализа явление рассматривается часто на качественном уровне. Исследователи оперируют обобщенными понятиями, как например, уровень и качество жизни, уровень образования и здравоохранения, результативность хозяйственной деятельности и т.п. При построении модели будет использоваться информация, наборы показателей, которые выражают эти явления, их свойства и взаимосвязи в виде количественных характеристик. Обычно в ряде эконометрических исследований такие системы показателей не могут быть сформированы однозначно, и одно и тоже явление может быть выражено альтернативными вариантами показателей. Например, уровень и качество жизни могут быть выражены среднедушевым доходом, индексом потребительских цен, коэффициентом рождаемости, продолжительностью жизни и т.д. Эффективность хозяйственной деятельности может быть охарактеризована набором таких показателей, как доля рынка, уровень затрат на рубль произведенной продукции, фондоотдача, чистая прибыль, балансовая прибыль и т.д.

Нетрудно заметить, что показатели, выражающие одну и ту же причину, могут быть сильно связаны между собой, например, рентабельность в основном зависит от затрат на производство, среднедушевой доход от уровня заработной платы т.д. В связи с этим одновременное включение таких факторов в модель нецелесообразно, поскольку одна и та же причина будет учтена дважды. Поэтому к проблеме обоснования системы показателей эконометрической модели необходимо относиться с вниманием, так как неправильный выбор показателей может повлиять на качество модели. Кроме того заметим, что часто успех или неудача в моделировании определяются не только правильностью выбора данных, но и их доступностью и точностью.

При отборе параметров модели (зависимой переменной y и независимых факторов x_i) исследователь опирается на имеющиеся экономические теории, спе­циальные знания или на интуитивные представления об анализируемой экономической системе. Необходимым условием эконометрического моделирования яв­ляется понимание сути хозяйственной деятельности, специ­фики взаимосвязей и законов ее развития. Как правило, зависимости между экономическими явлениями очень сложны. Учесть в модели все факторы практически невозможно, к тому же многие факторы имеют эпизодический или случайный характер. В число объясняющих факторов в эконометрическую модель включаются только важнейшие, наиболее существенные, менее значимые факторы игнорируются. Внешнее представление зависимости между показателями имеет вид уравнения модели.

Рассматривая проблему выбора конкретного вида зависимости между показателями, заметим, что для любой формы зависимости можно подобрать целый ряд уравнений, которые в определенной степени будут описывать эти связи. Тип уравнения может отражать либо определенную экономическую концепцию, лежащую в основе взаимосвязи между зависимой и независимыми переменными, либо эмпирические, т.е. выявленные в ходе конкретного исследования взаимосвязи между ними. Существуют различные экономические теории, относящиеся либо к экономике в целом, либо к отдельному рынку, либо к фирме, на основе которых могут формулироваться гипотезы о том, что некоторая зависимость может быть приближенно описана определенной аналитической функцией.

Например, в основе использования линейной формы модели лежит предположение о постоянстве приростов зависимой переменной y относительно зависимых переменных . Параметры прих_i характеризуют среднее изменение результата при изменении соответствующего фактора на единицу, при неизменном значении других факторов, закрепленных на среднем уровне. В качестве экономического примера можно привести зависимость переменных затрат предприятия от непосредственного объема выпускаемой продукции (расход материала, оплата труда и т.д.)

В эконометрических исследованиях широко используется степенная функция. Из экономической теории известно, что если эластичность зависимой переменной y относительно объясняемых переменных постоянна, то модель должна иметь степенную форму. В этой модели показатель степени при переменнойх_i является коэффициентом эластичности и показывает, на сколько процентов изменяется результат с изменением соответствующего фактора на один процент при неизменности действия других факторов. Степенная функция наибольшее распространение получила в исследовании спроса и потребления, в производственных функциях.

Двухфакторная производственная функция Кобба-Дугласа:

применяется при анализе взаимосвязи между объемом выпускаемой продукции и используемыми ресурсами (трудовыми и материальными). Различные модификации производственных функций различаются в основном ограничениями, накладываемыми на значения коэффициентов, и могут быть построены как для всей национальной экономики, так и для отдельной отрасли и фирмы.

В практике эконометрического моделирования используется достаточно широкий круг функциональных зависимостей между переменными. Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации.

Для моделей парной регрессии выбор вида аналитической зависимости может быть осуществлен графически. Графически взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат – значения признака результативного. При отсутствии тесных связей имеет место беспорядочное расположение точек на графике (рис.7.1,а). При наличии связи точки будут группироваться вокруг определенной линии, отражающей форму связи (рис. 7.1,б,в). Очевидно, что наиболее подходящая форма обеспечивает наилучшее приближение теоретических значений (расчетных по модели) y к действительным значениям. Если полученный вариант модели не удовлетворяет критериям качества, можно попытаться сформировать другой вариант модели, отличающийся от предыдущего либо составом факторов, либо формой их взаимосвязи с зависимой переменной y.

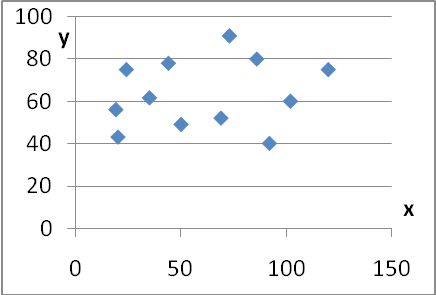
Рис. 7.1. Типы корреляции, а - отсутствие корреляции; б - сильная линейная корреляция;

в - сильная нелинейная корреляция.