4.3 Показатели измерения сезонности

Можно выделить два подхода в измерении сезонности: статистическое измерение сезонности и измерение с использованием специального математического аппарата - спектрального анализа. Сезонность характеризуется длительностью периода колебаний (отрезок времени между соседними точками максимума и минимума), амплитудой колебаний (разность между максимальными и минимальными значениями) и размещением максимумов и минимумов во времени. Статистическое измерение сезонности заключается в определении величины сезонных колебаний (сезонной волны) с помощью индексов сезонности.

Сезонная волна представляет собой совокупность исчисленных для каждого месяца (квартала) годового цикла индексов сезонности, характеризующих внутригодовую динамику явления. Для наглядного представления сезонную волну представляют в виде линейного графика. По сезонной волне определяется период колебаний, амплитуда, расположение максимумов и минимумов во времени. Если эти характеристики сезонной волны на протяжении длительного периода (нескольких лет) стабильны, то сезонная волна называется постоянной. На практике, как правило, такое предположение для большинства экономических процессов не выполняется. Для сезонной волны характерно изменение во времени ее формы и размаха, то есть сезонность носит переменный характер.

В зависимости от характера временного ряда методы, позволяющие рассчитать сезонные волны, делятся на две группы. К первой группе относятся методы, с помощью которых измерение сезонности производится по рядам без предварительного исключения тенденции. Это прежде всего метод простой средней и метод цепных индексов (метод Персонса).

Вторая группа методов расчета сезонной волны предусматривает определение общей тенденции развития временного ряда, вычисление сезонных колебаний и постоянной сезонной волны и, далее, расчет эволюции сезонной волны.

Общая тенденция временного ряда представляет собой плавное движение, сглаживающее, в первую очередь, периодические колебания по месяцам. Для расчета общей тенденции временного ряда применяются следующие методы: механические способы сглаживания (сглаживание по двум точкам, скользящая средняя), аналитические методы выравнивания с помощью математических функций и комбинированный способ (сочетание сглаживания с аналитическим методом выравнивания).

Способом сглаживания периодических колебаний по двум точкам устанавливается связь между начальным и конечным уровнем ряда, промежуточные точки выпадают из сферы исследования.

В методе скользящего среднего участвуют все точки ряда. Данный метод предполагает, что сезонные колебания взаимно погашаются на исследуемом отрезке времени. В волнообразных рядах этот метод приводит к искажениям основной тенденции динамики. Применение данного метода ограничено и рекомендуется применять центрированную скользящую среднюю или повторное сглаживание.

В основе выделения общей тенденции временного ряда с помощью методов аналитического выравнивания лежит предположение, что рассматриваемый ряд имеет некоторую закономерность, которая может быть аппроксимирована кривой. В качестве таких кривых наиболее часто используют полиномиальные, экспоненциальные и S–образные кривые. Сезонные колебания – это отклонения общей тенденции от эмпирического ряда. Эти отклонения могут быть определены как абсолютные, относительные и нормированные величины.

Рассмотрим экономический процесс, представленный временным рядом, подверженный периодическим колебаниям, имеющим постоянный период, равный годовому промежутку. Такой ряд называется тренд-сезонным временным рядом.

Тренд-сезонный временной ряд можно представить в аддитивной и мультипликативной форме. Тренд-сезонный временной ряд, порождаемый аддитивным случайным процессом представляется как:

, , (4.10)

где - тренд (регулярная компонента);

- сезонная компонента;

- случайная компонента.

Для случайной компоненты сделаем предположение, что его математическое ожидание равно нулю, дисперсия постоянна и автокорреляция между соседними уровнями ряда отсутствует:

, .

Предполагается, что сезонная компонента V_tимеет периодТ₀, то есть

V_t+Т0=V_t, Т₀=12 для месячных данных и Т₀=4 для квартальных данных.

Т=mТ₀ – величина Т₀ содержится в Т целое число раз m.

Временной ряд удобно задать матрицей [Y_ij] размера mxТ₀ :

, ,.

Связь между индексами t и ij можно представить следующим образом:

, .

Мультипликативная модель сезонного временного ряда имеет вид:

, (4.11)

где - “годовая” составляющая (тренд);

- постоянная пропорциональности для j-го месяца (квартала), не меняющаяся от года к году;

- случайная ошибка.

Если амплитуда сезонной волны относительно постоянна, то временной сезонный ряд можно представить в виде аддитивной модели, в случае, если сезонные колебания пропорциональны среднему значению, то возможно использование мультипликативной модели.

Рассмотрим показатели, применяемые для измерения сезонности. Самый простой способ измерения сезонности состоит в вычисление удельного веса уровней исследуемых показателей в суммарном годовом уровне. Если полученные значения усреднить по одноименным фазам года (месяцам, кварталам) за несколько лет, то получится более устойчивая оценка.

Вторым способом широко применяемым в статистической литературе является использование индексов сезонности:

,

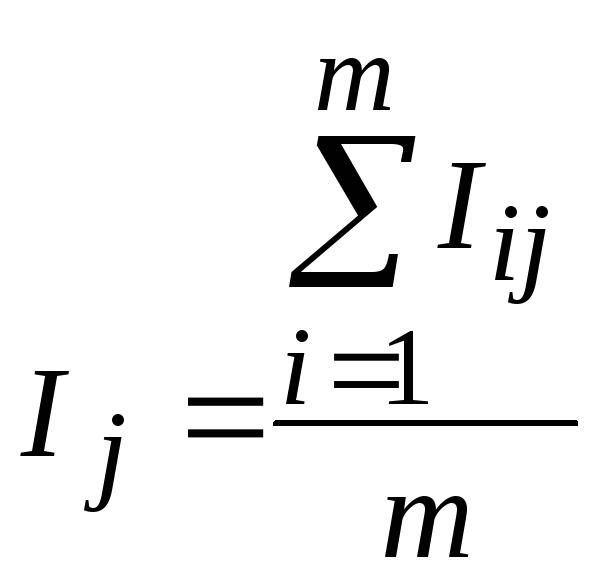где ,

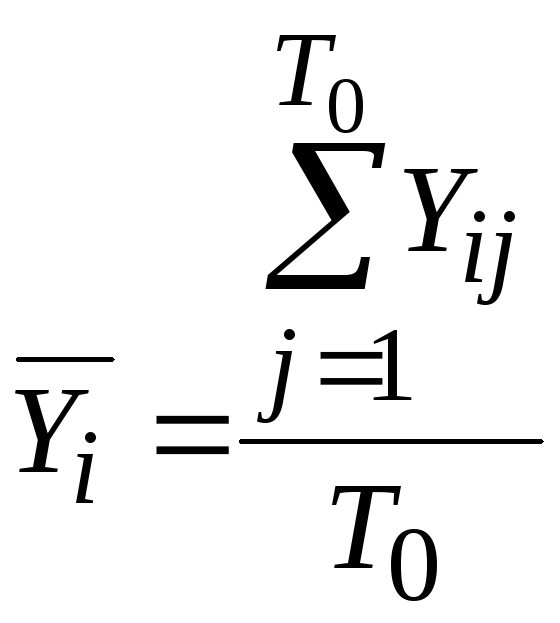
Индексы сезонности можно оценить и более точно, если известно значение тренда:

.

Индексы сезонности характеризуют степень отклонения уровня сезонного временного ряда от тренда. Чаще всего рассматривают не ряд относительных показателей, а ряд процентов. Так как производится усреднение индексов за анализируемый период, индексы сезонности дают представление о средней сезонной волне.

Факторы, формирующие сезонные колебания, в динамике изменяются, это приводит к эволюции сезонной волны. Известны три типа эволюции сезонной волны: изменение характера сезонной волны при постоянной амплитуде колебаний (качественная эволюция), изменение амплитуды сезонной волны при постоянном характере сезонности (количественная эволюция), изменение характера и амплитуды сезонной волны. Первый тип эволюции сезонной волны имеет место в случае, если влияние формирующего фактора переместилось от одного месяца к другому. Второй тип эволюции сезонной волны наблюдается в случае усиления или ослабления формирующих факторов. Третий тип эволюции возникает в результате появления новых факторов или изменения интенсивности воздействия старых факторов и перемещения их влияния от одного месяца к другому.

Для оценки уровня сезонности в каждом году используется ряд коэффициентов.

Коэффициент сезонности характеризует степень аритмии производственных процессов и недогрузки производственных мощностей, то есть показывает негативное влияние сезонности на производство. Коэффициент сезонности вычисляется как отношение недопроизведенной из-за сезонности продукции к потенциально возможному объему при ее отсутствии (рис. 4.5):

,

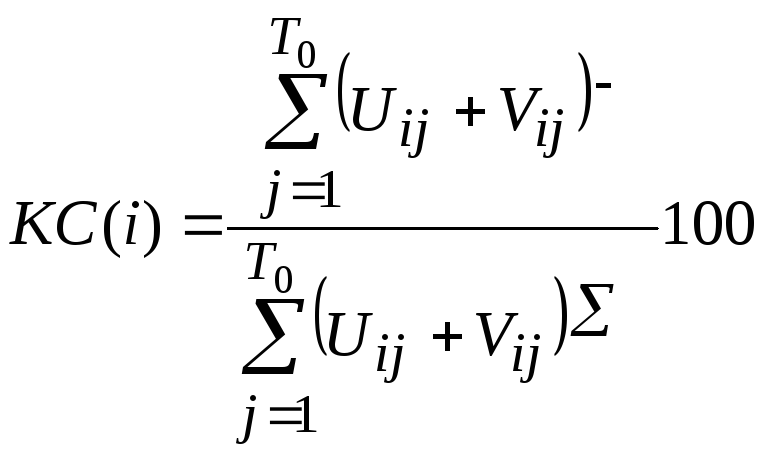где - ординаты огибающей, проходящей через соседние точки максимума,

- на рисунке это площадь фигуры более темно окрашенной.

На рисунке площадь соответствует режиму развития системы без сезонных колебаний и задается максимальными значениями.

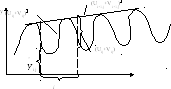
Рис. 4.5. Иллюстрация к расчету коэффициента сезонности

Коэффициент напряженности сезонной волны отражает изменение амплитуды сезонной волны по отношению к базовому уровню:

.

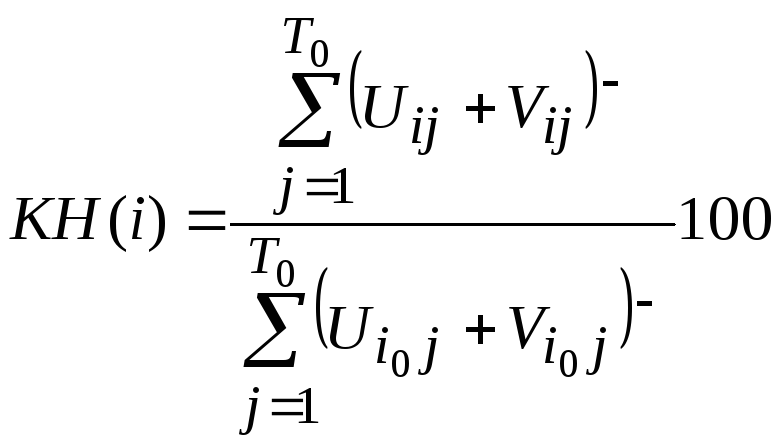Коэффициент напряженности дает представление о темпах развития сезонной волны и позволяет анализировать динамику волны.

Коэффициент роста служит для описания динамики процессов, свободных от сезонных колебаний:

.

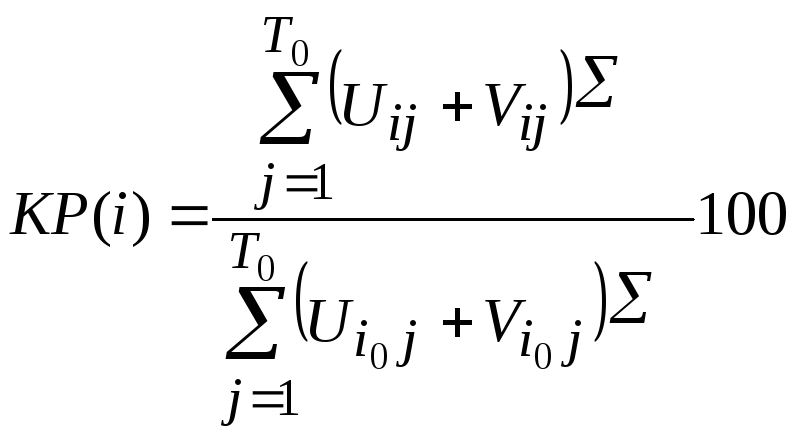Для описания сезонности используют показатели глубины сезонности абсолютные и относительные:

,

,,

где ,,.

Метод спектрального анализа рассматривает временной ряд как вероятностную модель случайного процесса с дискретным временем и исследует стационарные процессы для которых характерно отсутствие тренда.

Рис. 4.6. Периодический временной ряд

Спектральный анализ характеризует временной ряд не во временном, а в частотном аспекте. Стационарный временной ряд (рис. 4.6) можно задать четырьмя параметрами: периодом (или частотой), амплитудой, фазой и средним значением. Период (Т) – интервал времени через который временной ряд повторяется. Период измеряется числом единиц времени за цикл. Частота - величина, обратная периоду (f=1/T), указывает число повторений цикла в единицу времени и измеряется числом циклов в единицу времени. Угловая частота - =2f, измеряется в радианах в единицу времени. Амплитуда (А) – это отклонение от среднего значения ряда до пика или впадины. Фаза () – это расстояние между началом отсчета времени и ближайшим пиковым значением.

Таким образом, стационарный периодический ряд можно записать в форме:

,

где  – среднее значение ряда, которая называется гармоническим представлением. Данное уравнение часто записывают через тригонометрические функции косинусов и синусов без явного упоминания о фазе:

,

где ,.

Практически задача выделения периодичностей состоит в аппроксимации исходного процесса рядом косинусоид и синусоид, то есть рядом Фурье, при котором период колебаний известен.

Методы определения сезонности, основанные на разных теоретических предпосылках, дают неодинаковые результаты. Точность расчета сезонной волны может быть проверена в результате анализа временного ряда. Если сезонная волна рассчитана достаточно точно, то после ее элиминирования во временном ряду не должно остаться периодических колебаний. Сезонные колебания могут остаться во временном ряду по двум причинам. Во-первых, если сезонная волна недостаточно полно учитывает сезонный компонент. И, во-вторых, если сезонная волна включает в себя несистематические отклонения.

Для оценки точности сезонной компоненты не существует единого универсального критерия. Обычно применяется несколько методов проверки. Наиболее простой метод оценки заключается в сопоставлении средних исходного ряда и ряда, скорректированного на сезонность по периодам (годам). Если сезонные колебания определены правильно, то положительные и отрицательные сезонные колебания от среднего уровня взаимно погашаются, и уровни рядов совпадают. Расхождение между средними допускается обычно в пределах 10%.

По второму методу из временного ряда, скорректированного на сезонность, исключают влияние тренда. Если остаточные значения за отдельные периоды случайны, то сезонный компонент вычислен точно. Данный метод приемлем, если в сезонных колебаниях нет систематических сдвигов.

Третий метод состоит в сопоставлении смежных значений временного ряда, скорректированного на тренд и сезонность. Частные от деления этих скорректированных данных за смежные периоды должны случайно отклоняться от 1. Данный метод не дает определенного критерия для решения вопроса о правильном определении сезонных колебаний, но предоставляет возможность ранжировать методы расчета сезонных колебаний. Наилучшим методом считается тот, в котором указанные отклонения ближе всего к 1.

Четвертым методом определяется точность расчета сезонной волны путем сравнения дисперсии членов скорректированного ряда на сезонность по периодам (годам). Наиболее точной считается та сезонная волна, скорректированный ряд которой имеет наименьший показатель дисперсии.

Применение того или иного метода расчета сезонной волны зависит от цели исследования, наличия исходной информации, требуемой степени точности расчета сезонных колебаний. Если для анализа необходимо установить факт сезонности, то достаточно применить наиболее простые методы, для прогноза применяются более точные методы определения сезонных колебаний и измерения их эволюции.

Пример.

Проведем анализ временного ряда, характеризующего задолженность ОАО «Черметпром» перед банками. ОАО «Черметпром» является производителем чугуна. На мировом рынке спрос на чугун увеличивается в осенний период. Собственных средств у предприятия в момент наивысшего спроса недостаточно, и оно вынуждено брать кредиты в банке.

1 год	Задолжен-ность перед банками, тыс. руб.	2 год	Задолжен-ность перед банками, тыс. руб.	3 год	Задолжен-ность перед банками, тыс. руб.
Январь	58792	Январь	129664	Январь	258875
Февраль	32792	Февраль	132663	Февраль	322800
Март	34215	Март	134226	Март	320350
Апрель	35571	Апрель	132208	Апрель	334320
Май	37713	Май	140208	Май	299800
Июнь	36155	Июнь	138908	Июнь	301747
Июль	34572	Июль	115655	Июль	316236
Август	198155	Август	353155	Август	658927
Сентябрь	203055	Сентябрь	405055	Сентябрь	672316
Октябрь	224055	Октябрь	423055	Октябрь	672018
Ноябрь	230215	Ноябрь	402255	Ноябрь	670480
Декабрь	170335	Декабрь	136335	Декабрь	302590

Сезонные колебания могут проявляться, например, на месячных данных и полностью нивелироваться на данных другой периодичности (годовой, квартальной). Поэтому для выявления сезонных колебаний требуются временные ряды соответствующей периодичности и длины, поскольку оценка сезонных колебаний существенно затрудняется при коротких периодах наблюдений.

Перечисленные выше данные представим в виде простых графиков (рис.4.7) и графиков, построенных методом наложения (рис. 4.8). Данный метод построения графика позволяет более отчетливо выявить сезонные колебания, свойственные данному исследуемому процессу.

Рис.4.7. Задолженность ОАО «Черметпром» перед банками

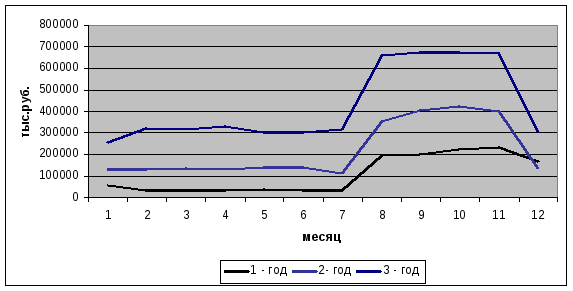
Рис.4.8. Задолженность ОАО «Черметпром» перед банками

В данном случае анализ сезонности проведем с помощью индексов сезонности, которые показывают зависимость уровня ряда от сезонного изменения экономической конъюнктуры. Так как в ряду динамики наблюдается повышающийся тренд, то необходимо произвести аналитическое выравнивание ряда. В качестве аппроксимирующего полинома выбран полином второго порядка: .Результаты аппроксимации временного ряда полиномом представлены в таблице 4.5.

Таблица 4.5

Аппроксимация временного ряда «Задолженность ОАО «Черметпром» перед банками» и расчет индексов сезонности

Время
1	58792.000	51037.116	7754.884	115.19
2	32792.000	56379.234	-23587.234	58.16
3	34215.000	62262.900	-28047.900	54.95
4	35571.000	68688.113	-33117.113	51.79
5	37713.000	75654.871	-37941.871	49.85
6	36155.000	83163.176	-47008.176	43.47
7	34572.000	91213.027	-56641.027	37.90
8	198155.000	99804.422	98350.578	198.54
9	203055.000	108937.367	94117.633	186.40
10	224055.000	118611.852	105443.148	188.90
11	230215.000	128827.891	101387.109	178.70
12	170335.000	139585.473	30749.527	122.03
13	129664.000	150884.602	-21220.602	85.94
14	132663.000	162725.275	-30062.275	81.53
15	134226.000	175107.496	-40881.496	76.65
16	132208.000	188031.266	-55823.266	70.31
17	140208.000	201496.578	-61288.578	69.58
18	138908.000	215503.438	-76595.438	64.46
19	115655.000	230051.844	-114396.844	50.27
20	353155.000	245141.797	108013.203	144.06
21	405055.000	260773.297	144281.703	155.33
22	423055.000	276946.344	146108.656	152.76
23	402255.000	293660.930	108594.070	136.98
24	136335.000	310917.063	-174582.063	43.85
25	258875.000	328714.750	-69839.750	78.75
26	322800.000	347053.980	-24253.980	93.01
27	320350.000	365934.758	-45584.758	87.54
28	334320.000	385357.078	-51037.078	86.76
29	299800.000	405320.945	-105520.945	73.97
30	301747.000	425826.359	-124079.359	70.86
31	316236.000	446873.328	-130637.328	70.77
32	658927.000	468461.828	190465.172	140.66
33	672316.000	490591.891	181724.109	137.04
34	672018.000	513263.484	158754.516	130.93
35	670480.000	536476.625	134003.375	124.98
36	302590.000	560231.328	-257641.328	54.01

Индекс сезонности определим как отношение фактических уровней и сглаженных уровней: (таб. 4.5).Для устранения факторов случайного порядка проведем усреднение индексов сезонности по одноименным месяцам: (таб.4.6).

Таблица 4.6.

Индексы сезонности

Месяц
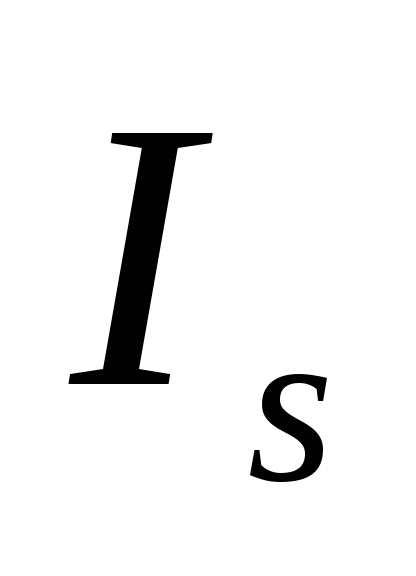
Январь	93.29472
Февраль	77.56683
Март	73.04963
Апрель	69.61795
Май	64.46604
Июнь	59.59791
Июль	52.98076
Август	161.0875
Сентябрь	159.5888
Октябрь	157.5284
Ноябрь	146.8858
Декабрь	73.2967

Графическое изображение индексов сезонности – сезонная волна - представлены на рис. 4.9. По рисунку хорошо видно, что спрос на заемные ресурсы сильно возрастает в августе-ноябре.

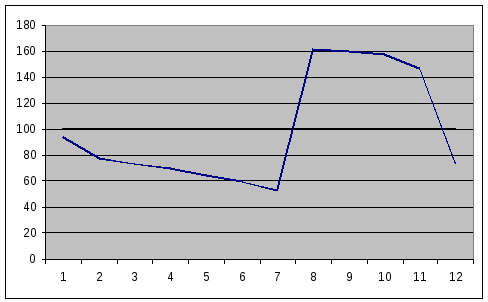
Рис. 4.9. Сезонная волна задолженности ОАО «Черметпром»

перед банками

Интенсивность колебаний измерим с помощью коэффициента колеблемости (таб. 4.7), который определяется как отношение среднего квадратического отклонения от тренда к среднему уровню временного ряда:

.

Таблица 4.7

Расчет коэффициента колеблемости

Время
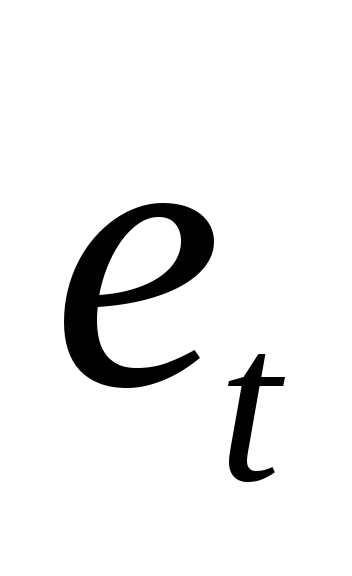
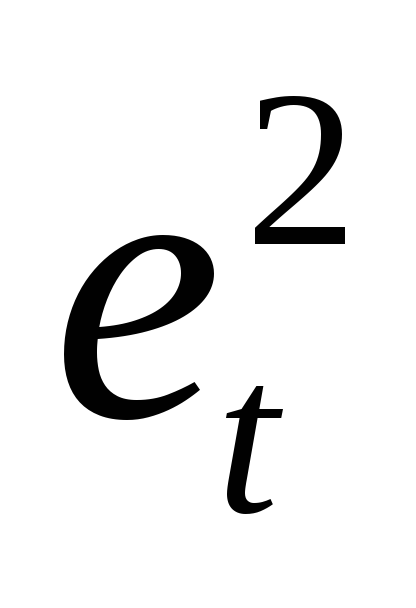
1	7754.884	60138230.15
2	-23587.234	556357625.5
3	-28047.900	786684716.3
4	-33117.113	1096743192
5	-37941.871	1439585582
6	-47008.176	2209768590
7	-56641.027	3208205979
8	98350.578	9672836218
9	94117.633	8858128806
10	105443.148	11118257552
11	101387.109	10279345947
12	30749.527	945533431.9
13	-21220.602	450313930.7
14	-30062.275	903740401.7
15	-40881.496	1671296723
16	-55823.266	3116236985
17	-61288.578	3756289809
18	-76595.438	5866861046
19	-114396.844	13086637860
20	108013.203	11666852049
21	144281.703	20817209857
22	146108.656	21347739431
23	108594.070	11792672107
24	-174582.063	30478896547
25	-69839.750	4877590680
26	-24253.980	588255568.6
27	-45584.758	2077970145
28	-51037.078	2604783344
29	-105520.945	11134669900
30	-124079.359	15395687423
31	-130637.328	17066111500
32	190465.172	36276981697
33	181724.109	33023651928
34	158754.516	25202996231
35	134003.375	17956904511
36	-257641.328	66379053958

.

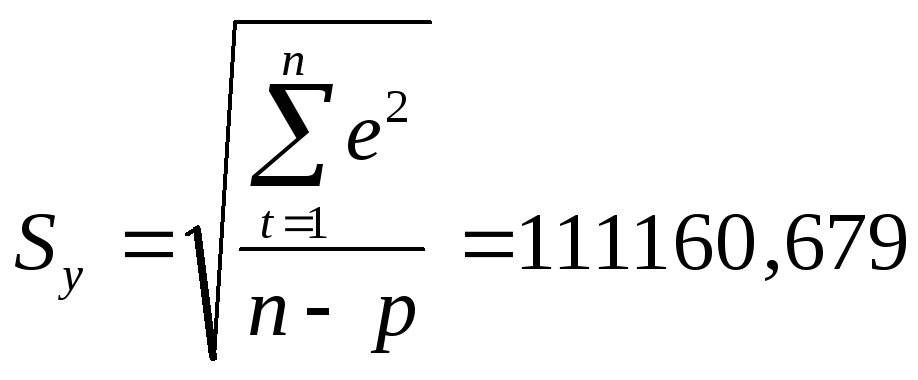или 44,12%

Для изучаемого временного ряда величина коэффициента колеблемости составила 44,12%, колеблемость можно охарактеризовать как очень сильную. Это еще раз подтверждает необходимость учета сезонности при моделировании финансовых процессов.