
3.Ур. и нер-ва с модулем
.doc§3. УРАВНЕНИЯ И НЕРАВЕНСТВА, СОДЕРЖАЩИЕ НЕИЗВЕСТНУЮ ПОД ЗНАКОМ АБСОЛЮТНОЙ
ВЕЛИЧИНЫ (МОДУЛЯ)
Абсолютная
величина (модуль) действительного числа
![]() определяется
следующим образом:
определяется
следующим образом:
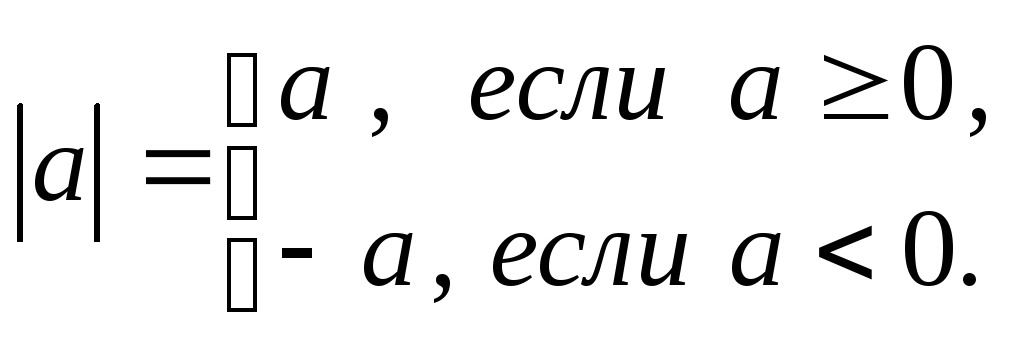 Основные
свойства
абсолютной величины действительных
чисел:
Основные
свойства
абсолютной величины действительных
чисел:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() (модуль произведения);
(модуль произведения);
г)
![]() ,
,
![]() (модуль дроби);
(модуль дроби);
д)
![]() (неравенство треугольника или модуль
(неравенство треугольника или модуль
суммы). Здесь неравенство обращается в равенство тогда и только тогда, когда слагаемые имеют одинаковый знак.
1)
Уравнение вида
![]() (1)
можно
заменить совокупностью систем двумя
способами.
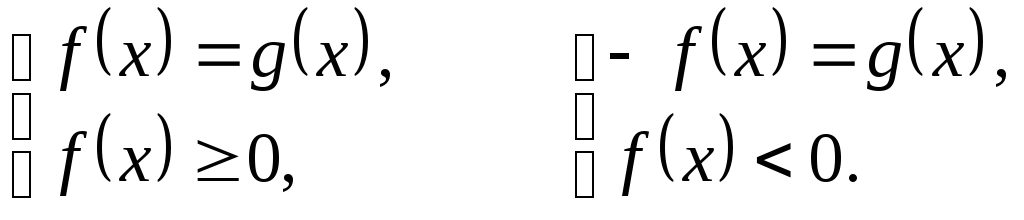
П е р в ы й с п о с о б.
Уравнение (1) равносильно совокуп-
ности
систем:
(1)
можно
заменить совокупностью систем двумя
способами.
П е р в ы й с п о с о б.
Уравнение (1) равносильно совокуп-
ности
систем:
 В т о р о й с п о с о б. Уравнение (1)
равносильно совокуп-
ности систем:
В т о р о й с п о с о б. Уравнение (1)
равносильно совокуп-
ности систем:
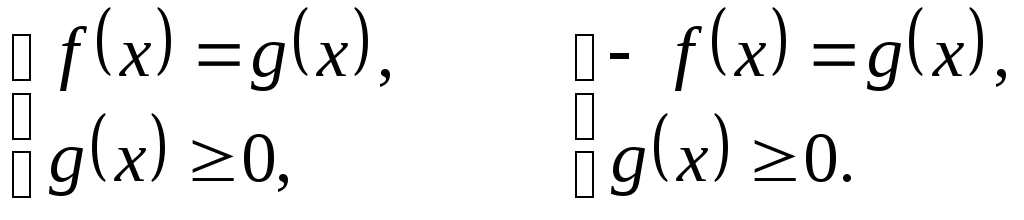
22
Если
в уравнении (1) функция
![]() имеет более простой
вид, чем
имеет более простой
вид, чем
![]() ,
то применяют первый способ, а если
наоборот, то – второй способ.
В
частности, уравнение вида
,
то применяют первый способ, а если
наоборот, то – второй способ.
В
частности, уравнение вида
![]() ,
при
,
при
![]() решений не имеет; при
решений не имеет; при
![]() равносильно уравне- нию
равносильно уравне- нию
![]() ;
при
;
при
![]() равносильно совокупности уравнений
равносильно совокупности уравнений
![]() 2)
2)
![]()
![]()
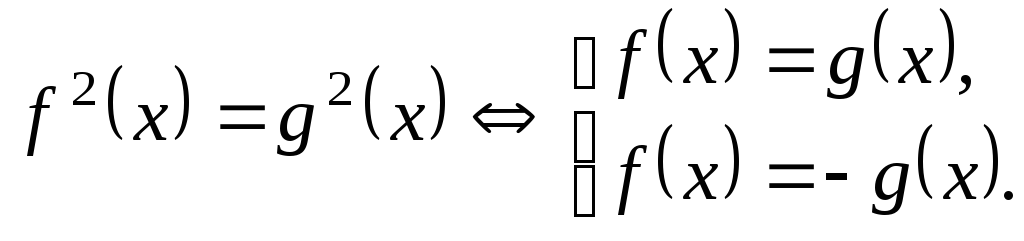 3) Уравнение вида
3) Уравнение вида
![]() ,
где
,
где![]() – некоторые функции, реша-
ется методом
интервалов. Для этого находят сначала
все точки, в которых хотя бы одна из
функций
– некоторые функции, реша-
ется методом
интервалов. Для этого находят сначала
все точки, в которых хотя бы одна из
функций
![]() меняет
знак. Эти точки делят область
допустимых
значений
меняет
знак. Эти точки делят область
допустимых
значений
![]() на промежутки, на каждом из ко-
торых
все функции
на промежутки, на каждом из ко-
торых
все функции![]() сохраняют знак. За-
тем, используя
определение модуля, раскрывают все
модули на каждом из найденных промежутков
и решают получен-
ные уравнения.
Объединение найденных решений составля-
ет
множество решений заданного уравнения.
Пример 1.
Найти сумму корней уравнения
сохраняют знак. За-
тем, используя
определение модуля, раскрывают все
модули на каждом из найденных промежутков
и решают получен-
ные уравнения.
Объединение найденных решений составля-
ет
множество решений заданного уравнения.
Пример 1.
Найти сумму корней уравнения
![]() .
Решение.
Данное уравнение
равносильно совокупности двух систем:
.
Решение.
Данное уравнение
равносильно совокупности двух систем:
а)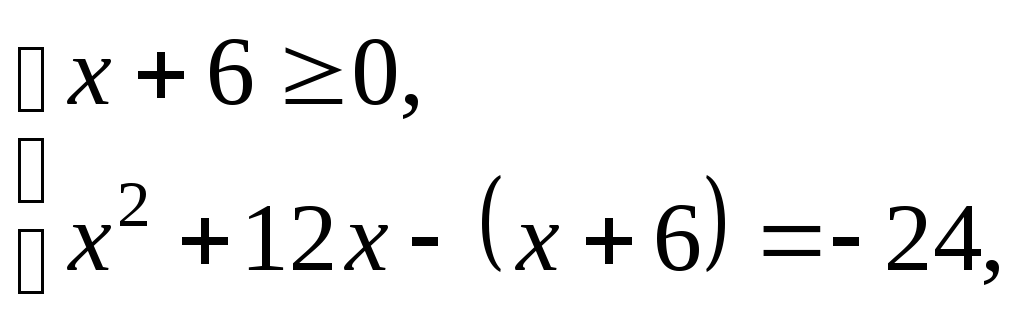 т.е.
т.е.
23
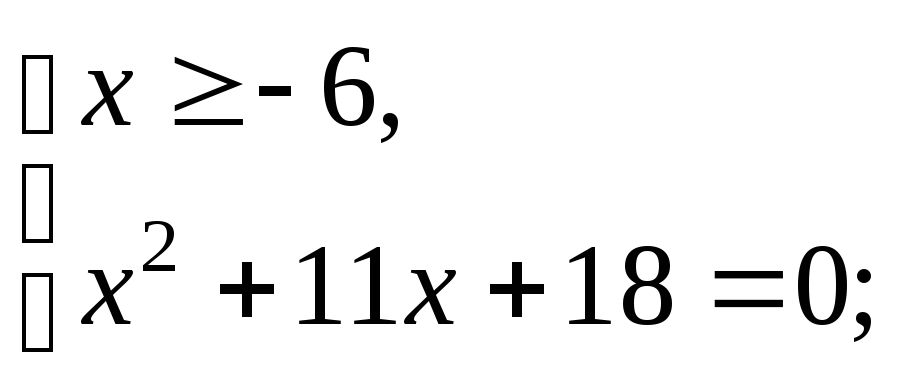 (2)
(2)
б)
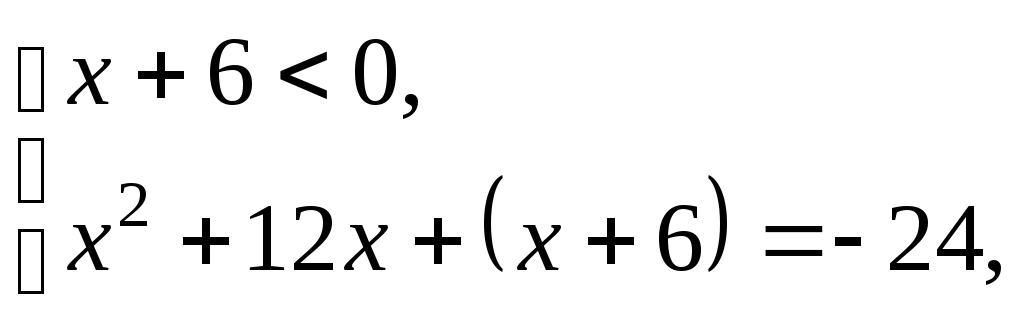 т.е.
т.е.
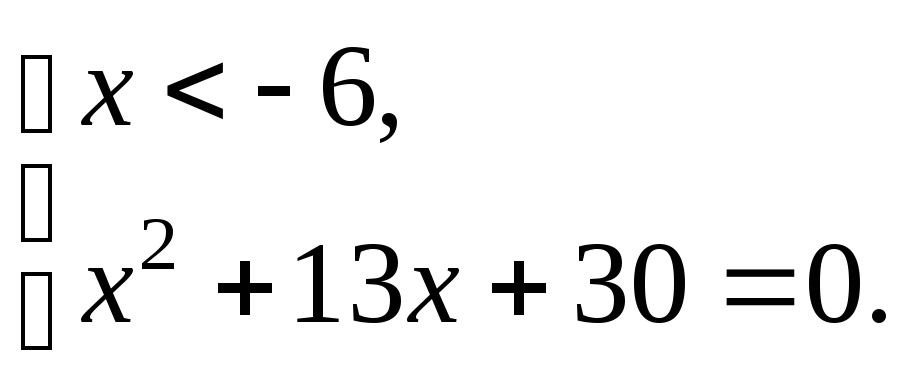 (3)
(3)
Уравнение
![]() имеет корни
имеет корни
![]() и
и
![]() ,
из которых только
,
из которых только
![]() является решением системы (2). Уравнение
является решением системы (2). Уравнение
![]() имеет корни
имеет корни
![]() и
и
![]() ,
из которых решением системы (3) является
только
,
из которых решением системы (3) является
только
![]() .
.
Таким
образом, исходное уравнение имеет два
корня:
![]() и
и
![]() .
.
![]() .
Ответ:
.
Ответ:
![]() .
Пример 2.
Найти
наибольшее целое решение уравнения
.
Пример 2.
Найти
наибольшее целое решение уравнения
![]() .
(4)
.
(4)
Решение.
Функция
![]() меняет знак в точке
меняет знак в точке
![]() ,
а функция
,
а функция
![]() – в точке
– в точке
![]() .
Этими точками ОДЗ уравнения (4) (интервал
.
Этими точками ОДЗ уравнения (4) (интервал
![]() ) разбивается на три промежутка:
) разбивается на три промежутка:
![]() .
В первом промежутке
.
В первом промежутке
![]() ;
во втором
про-
межутке
;
во втором
про-
межутке
![]() ;
в третьем промежутке
;
в третьем промежутке
![]() .
Следовательно, уравнение (4) равносиль-
но
совокупности трех систем:
.
Следовательно, уравнение (4) равносиль-
но
совокупности трех систем:
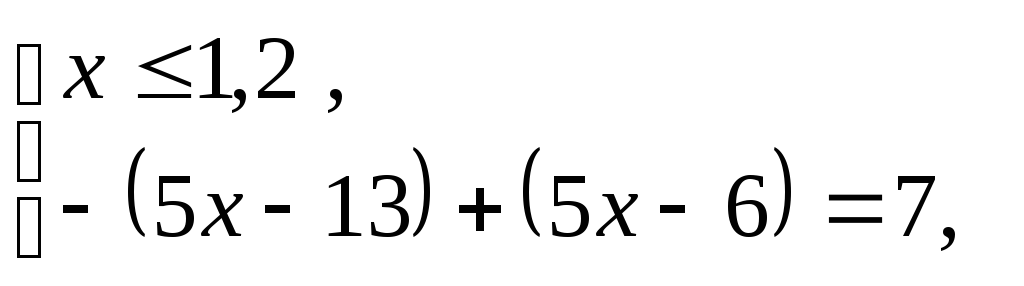
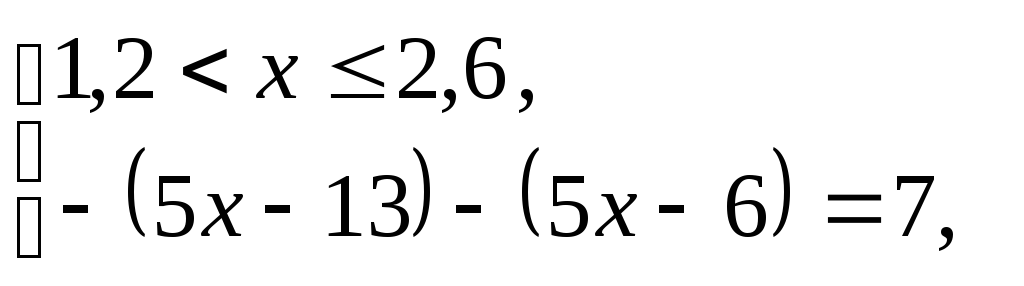
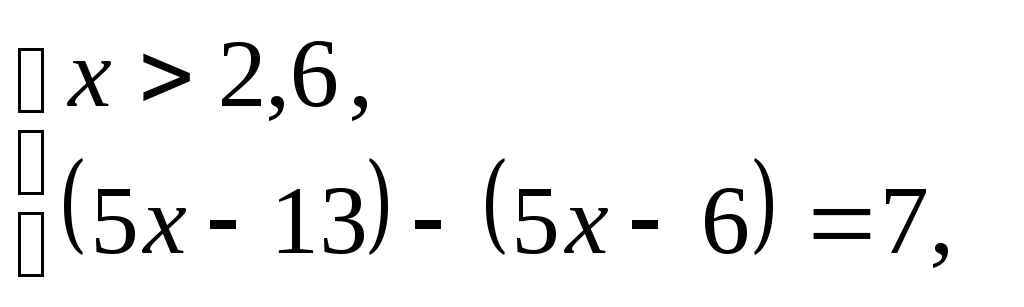 т.е.
совокупности систем
т.е.
совокупности систем
24
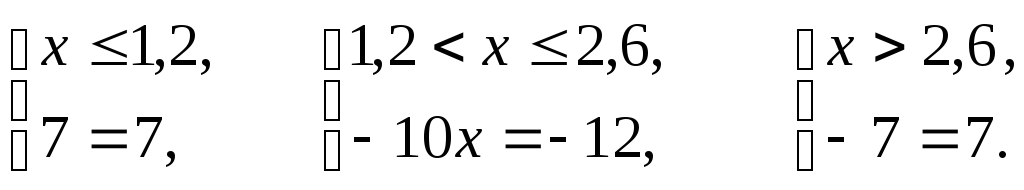 Решением
первой системы являются все числа из
промежутка
Решением
первой системы являются все числа из
промежутка
![]() .
Вторая и третья системы решений не
имеют.
Итак, множеством всех решений
исходного уравнения яв-
ляется
промежуток
.
Вторая и третья системы решений не
имеют.
Итак, множеством всех решений
исходного уравнения яв-
ляется
промежуток
![]() .
Наибольшее целое решение:
.
Наибольшее целое решение:
![]() .
Ответ:
1.
При решении
уравнения, в котором под знаком модуля
находится выражение, также содержащее
модуль, следует сначала освободиться
от внутренних модулей, а затем в полученных
уравнениях раскрыть оставшиеся модули.
Пример 3.
Найти сумму корней уравнения
.
Ответ:
1.
При решении
уравнения, в котором под знаком модуля
находится выражение, также содержащее
модуль, следует сначала освободиться
от внутренних модулей, а затем в полученных
уравнениях раскрыть оставшиеся модули.
Пример 3.
Найти сумму корней уравнения
![]() .
Решение.
Данное уравнение равносильно
совокупности
двух систем:
.
Решение.
Данное уравнение равносильно
совокупности
двух систем:
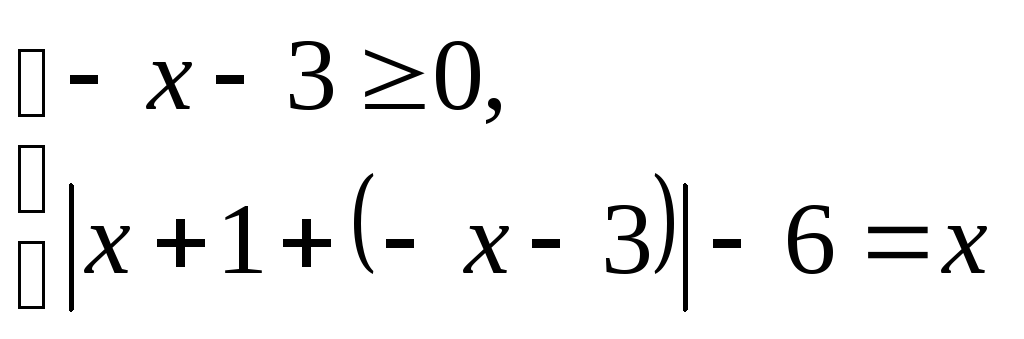 и
и
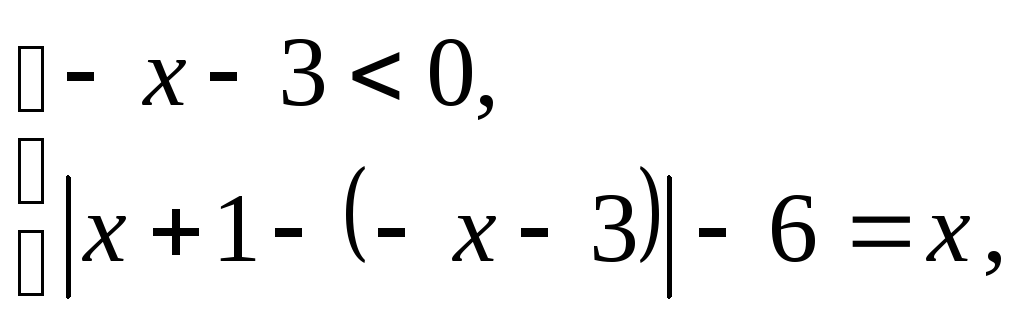 т.е.
т.е.
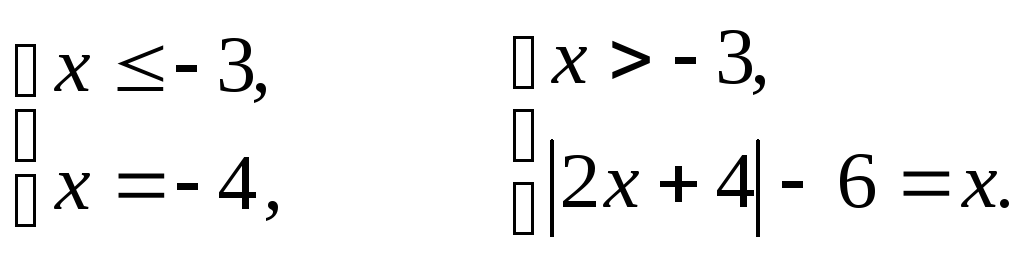 (5)
Решением первой
системы совокупности (5) является
число
(5)
Решением первой
системы совокупности (5) является
число
![]() .
Вторая система совокупности (5)
равносильна совокупнос-
ти двух
следующих систем:
.
Вторая система совокупности (5)
равносильна совокупнос-
ти двух
следующих систем:
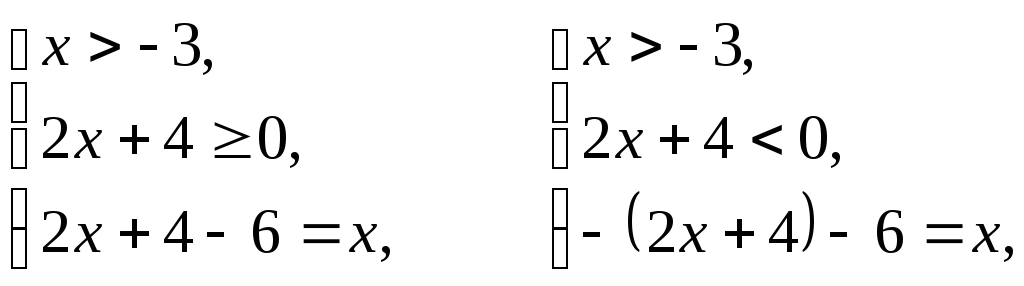 т.е.
т.е.
25
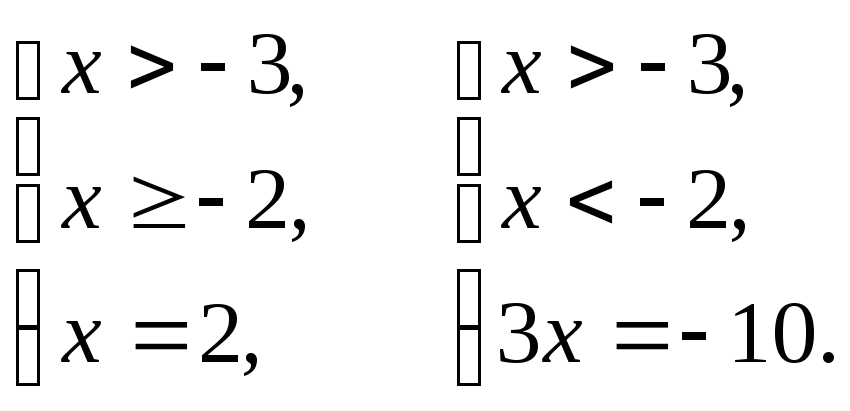 (6)
Решением первой
системы совокупности (6) является
число
(6)
Решением первой
системы совокупности (6) является
число
![]() ,
а вторая система решений не имеет.
Итак, исходное уравнение имеет два
корня:
,
а вторая система решений не имеет.
Итак, исходное уравнение имеет два
корня:
![]() .
Их сумма равна
.
Их сумма равна
![]() .
.
Ответ:
![]() .
.
4)
Основной метод при решении неравенств,
содержащих знак модуля, заключается в
следующем. ОДЗ неравенства разбивают
на части, на каждой из которых выражения,
стоящие под знаком модуля, сохраняют
знак. На каждой такой части решают
неравенство и полученные решения
объединяют в множество решений исходного
неравенства.
Пример 4.
Найти число целых решений неравенства:
![]() .
(7)
Решение.
ОДЗ неравенства
(7):
.
(7)
Решение.
ОДЗ неравенства
(7):
![]() .
.
Неравенство
(1) равносильно совокупности двух систем:
1)

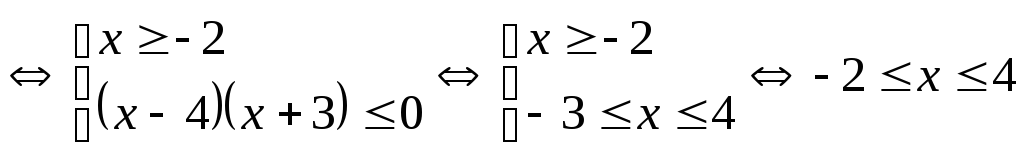 .
2)
.
2)

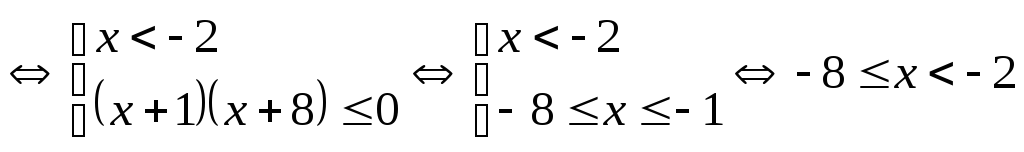 .
Множеством решений неравенства (7)
является объединение множеств
.
Множеством решений неравенства (7)
является объединение множеств
![]() и
и
![]() ,
т.е. отрезок
,
т.е. отрезок
26
![]() .
Этот отрезок содержит 13 целых чисел:
.
Этот отрезок содержит 13 целых чисел:
![]() .
.
Ответ:
![]() .
.
5)
Неравенство вида
![]() ,
где
,
где
![]() и
и
![]() – неко-
торые функции, можно решать
основным методом или сведением к
равносильному ему двойному неравенству:
– неко-
торые функции, можно решать
основным методом или сведением к
равносильному ему двойному неравенству:
![]() .
6) Неравенство
вида
.
6) Неравенство
вида
![]() можно решать основным методом или
заменой на равносильную ему совокупность
двух неравенств:
можно решать основным методом или
заменой на равносильную ему совокупность
двух неравенств:
![]()
![]() 7) Неравенства вида
7) Неравенства вида
![]() ,
(8)
и
,
(8)
и
![]() решаются методом
интервалов по той же схеме, что и
аналогичные уравнения.
Некоторые
неравенства вида (8) целесообразно
решать,
перейдя к равносильному
неравенству
решаются методом
интервалов по той же схеме, что и
аналогичные уравнения.
Некоторые
неравенства вида (8) целесообразно
решать,
перейдя к равносильному
неравенству
![]() .
Пример 5.
Найти длину интервала решений неравенства:
.
Пример 5.
Найти длину интервала решений неравенства:
![]() .
Решение.
Данное неравенство равносильно двойному
не-
равенству
.
Решение.
Данное неравенство равносильно двойному
не-
равенству
![]() ,
т.е. системе
,
т.е. системе
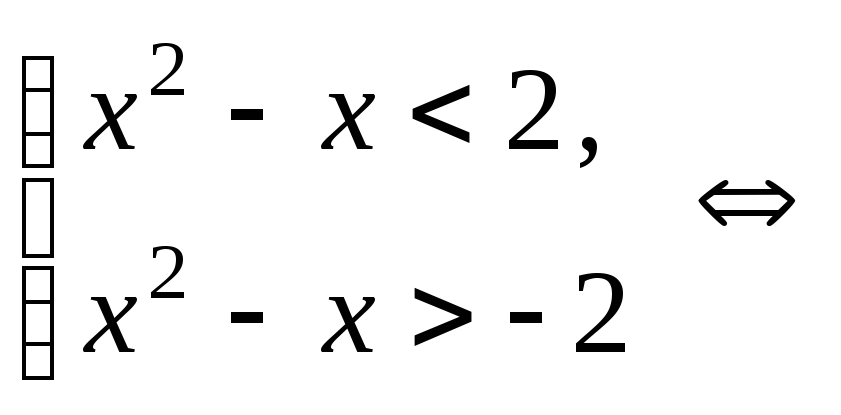
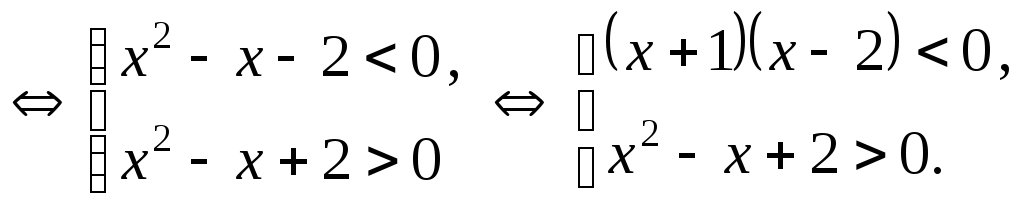
Неравенство
![]() выполняется при
выполняется при
![]() ,
а неравенство
,
а неравенство
![]() выполняется при любом
выполняется при любом
![]() ( т.к.
( т.к.
27
коэффициент при
![]() больше нуля и
больше нуля и
![]() ).
Таким образом, множество решений
исходного неравен-
ства есть интервал
).
Таким образом, множество решений
исходного неравен-
ства есть интервал
![]() .
Длина этого интервала:
.
Длина этого интервала:
![]() .
Ответ: 3.
Пример 6. Найти сумму целых решений
неравенства
.
Ответ: 3.
Пример 6. Найти сумму целых решений
неравенства
![]() ,
(9)
принадлежащих
отрезку
,
(9)
принадлежащих
отрезку
![]() .
.
Решение.
Неравенство (9) равносильно совокупности
двух
неравенств:
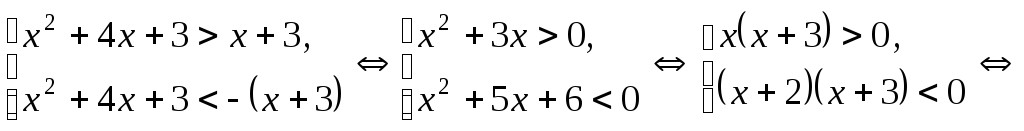
![]() Отсюда получаем множество решений
неравенства (9):
Отсюда получаем множество решений
неравенства (9):
![]() .
Из отрезка
.
Из отрезка
![]() это множество содержит следующие целые
числа: –15 ; –14 ; . . . ; – 4 ; 1 ; 2 ; 3 ; 4 ; . . .
; 15. Сумма этих чисел равна 6.
это множество содержит следующие целые
числа: –15 ; –14 ; . . . ; – 4 ; 1 ; 2 ; 3 ; 4 ; . . .
; 15. Сумма этих чисел равна 6.
Ответ:
6.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
1.
Найти наибольшее решение уравнения:
![]() .
(Ответ:
.
(Ответ:
![]() )
2.
Найти сумму корней уравнения:
а)
)
2.
Найти сумму корней уравнения:
а)
![]() ;
(Ответ:
;
(Ответ:
![]() )
)
б)
![]() ;
(Ответ:
;
(Ответ:
![]() )
)
в)
![]() .
(Ответ:
.
(Ответ:![]() )
)
28
3. Найти сумму
корней уравнения:
а)
![]() ;
(Ответ:
;
(Ответ:
![]() )
б)
)
б)
![]() ;
(Ответ: –
4)
в)
;
(Ответ: –
4)
в)
![]() .
(Ответ:
.
(Ответ:
![]() )
)
4. Решить уравнение:
а)
![]() ;
(Ответ: 2,75 ; 3,5)
б)
;
(Ответ: 2,75 ; 3,5)
б)
![]() ;
(Ответ:
;
(Ответ:
![]() )
в)
)
в)
![]() ;
(Ответ:
;
(Ответ:
![]() )
г)
)
г)
![]() ;
(Ответ:
;
(Ответ:
![]() )
д)
)
д)
![]() .
(Ответ:
.
(Ответ:
![]() )
)
5. Найти наименьшее
целое решение неравенства:
а)
![]() ;
(Ответ:
– 3)
б)
;
(Ответ:
– 3)
б)
![]() ;
(Ответ:
4)
в)
;
(Ответ:
4)
в)
![]() .
(Ответ:
4)
.
(Ответ:
4)
6. Найти сумму целых
решений неравенства:
а)
![]() ;
( Ответ:
;
( Ответ:
![]() )
б)
)
б)
![]() ;
(Ответ:
;
(Ответ:
![]() )
в)
)
в)
![]() ;
(Ответ:
;
(Ответ:
![]() )
г)
)
г)
![]() ;
(Ответ:
;
(Ответ:
![]() )
д)
)
д)
![]() ;
(Ответ:
;
(Ответ:
![]() )
)
29
е)
![]() .
( Ответ:
.
( Ответ:
![]() )
)
7. Решить неравенство:
а)
![]() ;
(Ответ:
;
(Ответ:
![]() )
)
б)
![]() ;
(Ответ:
;
(Ответ:
![]() )
)
в)
![]() ;
(Ответ:
;
(Ответ:
![]() )
)
г)
![]() ;
(Ответ:
;
(Ответ:
![]() )
)
д)
![]() .
(Ответ:
.
(Ответ:
![]() )
)
8. Найти сумму целых
значений
![]() ,
удовлетворяющих системе
неравенств:
а)
,
удовлетворяющих системе
неравенств:
а)
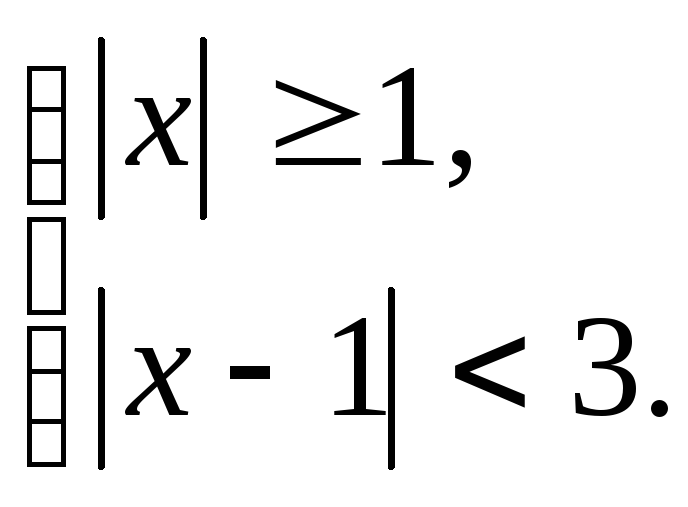 (
Ответ:
(
Ответ:
![]() )
б)
)
б)
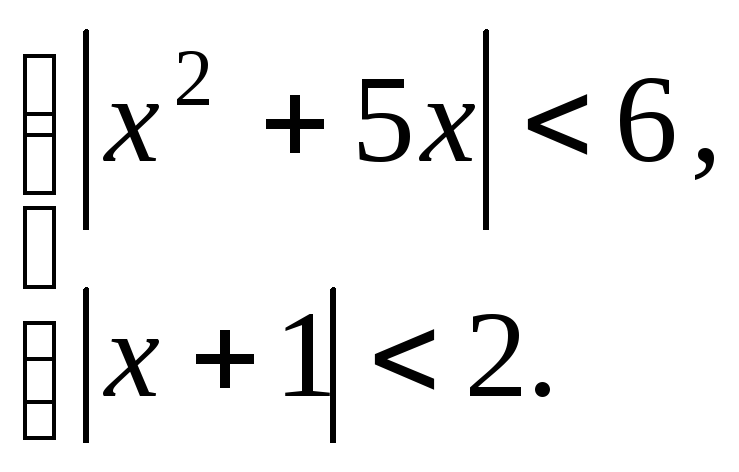 (Ответ:
(Ответ:
![]() )
)
30
