ЛЕКЦИЯ~2

Лекция 2

На примере уравнения мы видели, что все его решения могут быть заданы формулой . Семейство решений, определяемых этой формулой, называют общим решением данного дифференциального уравнения. Если задана точка , через которую должна проходить интегральная кривая уравнения, то этого можно добиться выбором постоянной . Выделенное решение, удовлетворяющее заданному начальному условию – частное решение.

Определение. Функция , зависящая от аргумента х и произвольной постоянной С, называется общим решением дифференциального уравнения (2) в области D, в которой выполнены условия теоремы Коши, если

1. для произвольного 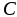функция есть решение уравнения (2);

2. для 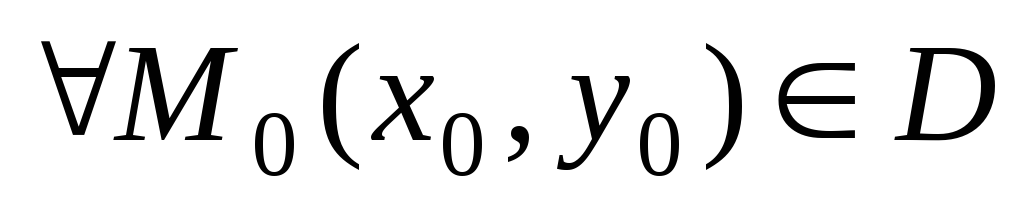существует единственное значение 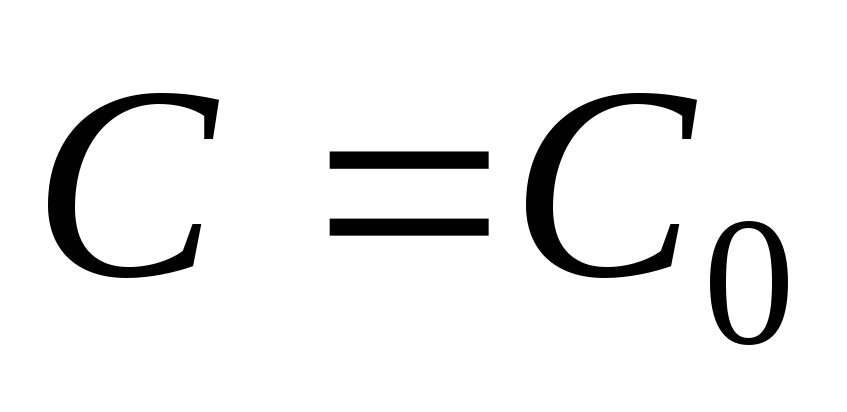такое, что .

Всякое решение, получающееся из общего при конкретном значении постоянной C, называется частным решением.

Замечание. Если общее решение удается найти в виде , не разрешенном относительно у, то его называют общим интегралом дифференциального уравнения.

Точки, в которых нарушаются условия теоремы Коши – особые точки. Через особую точку может не проходить ни одной интегральной кривой и в ней может нарушаться единственность решения. Если кривая целиком состоит из особых точек и является интегральной кривой дифференциального уравнения (2), то это особое решение. Для отыскания особого решения нужно найти кривую, в каждой точке которой нарушаются условия теоремы Коши и проверить, будет ли эта кривая решением уравнения (2).

Пример. Правая часть уравнения – непрерывная функция в , тогда как ее производная терпит разрыв при . Но – решение уравнения. Значит это особое решение.

Заметим, что особое решение не может быть получено из общего ни при каких значения постоянной С.

Методы интегрирования некоторых типов дифференциальных уравнений первого порядка.

1. Уравнения с разделяющимися переменными.

Уравнением с разделяющимися переменными называется уравнение вида

.

Разделив обе части этого уравнения на и умножив на , получим уравнение с разделенными переменными

. (1)

Считая у функцией от х и интегрируя по переменной х обе части последнего равенства, получим общий интеграл дифференциального уравнения (1):

. (2)

Отметим, что если , то – решение уравнения (1), которое не дается формулой (2).

Пример. Вернемся к задаче 1 из лекции 1. Разделяя переменные, получим

.

Так как по смыслу задачи , то. Найдем k и С из условий задачи.

.

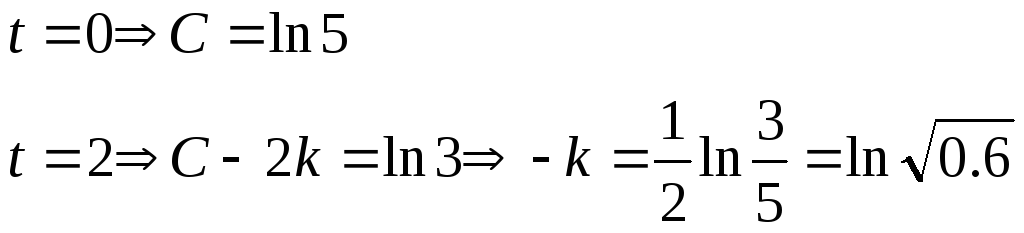Итак .

2. Однородное уравнение.

Дифференциальное уравнение называется однородным, если оно может быть представлено в виде

. (3)

Например, уравнение

является однородным. Однородным всегда является уравнение вида , где и – однородные многочлены одинаковой степени однородности:

. Здесь k – степень однородности. Например

.

Однородное уравнение (3) приводится к уравнению с разделяющимися переменными путем замены .

Получили общий интеграл дифференциального уравнения (3). Если из последнего соотношения удается выразить , то – общее решение этого уравнения.

Пример. Найти форму зеркала, собирающего все параллельные лучи в одну точку.

Очевидно, что зеркало должно иметь форму поверхности вращения, ось которой параллельна направлению падающих лучей. Примем эту ось за ось ОХ и найдем уравнение кривой , вращением которой образуется искомая поверхность. Начало координат поместим в точку О, в которой собираются отраженные лучи. Пусть КМ и МО – падающий и отраженный лучи. Проведем касательную МТ и нормаль МN к искомой кривой в точке М. Легко видеть, что МТО=ТМО (и оба равны 90⁰ –), то есть треугольник ТОМ равнобедренный. Поэтому |OM| = |OT|. Но |OM| = . Для нахождения ОТ составим уравнение касательной:

.

Значит . Получаем:

.

Последнее уравнение целесообразно привести к виду . Полагая , получим . Разделяя переменные, получим .

. Возвращаясь теперь к исходным переменным, окончательно имеем:

Таким образом, искомая кривая – парабола, а зеркало – параболоид вращения.

Уравнения, приводящиеся к однородным.

Уравнения вида

Приводятся к однородному уравнению подстановкой , где  и находятся из системы уравнений

.

Если определитель указанной системы равен нулю, то уравнение может быть сразу приведено к уравнению с разделяющимися переменными заменой

Пример. Найти общий интеграл уравнения

Переписав уравнение в виде

,

найдем  и  и выполним замену переменных:

Положим Тогда последовательно получим

3. Линейные уравнения

Линейным называется уравнение вида

(4)

где и – заданные непрерывные функции. Решение этого уравнения будем искать в виде произведения двух непрерывно дифференцируемых функций

(5)

Такой метод решения линейного уравнения был предложен Бернулли. Имеем

(6)

В качестве функции возьмем какое-либо решение уравнения

.

Положим С=0 и подставим найденное v в (6):

.

Итак:Нетрудно проверить, что найдено общее решение уравнения (4).

Пример. Вернемся к задаче 2 из лекции 1 и решим ее в случае, когда - число.

В этом случае для определения скорости получаем задачу Коши:

(7)

Уравнение в (7), очевидно, линейное. Его решение будем искать в виде произведения двух функций . Применяя изложенную выше схему рассуждений, последовательно получим:

Пусть – путь, пройденный телом за время t. Тогда

. Причем , поскольку

5