
KT Богомолов / МУ / ЗАДАНИЕ_3_СЛАУ мартицы / Решение систем линейных уравнений в Excel
.pdfРешение систем линейных уравнений в Excel
1. Введение
Многие задачи организации строительного производства сводятся к решению систем линейных уравнений вида:
a11x1 a12x2 a1nxn b1, |
|
||||||||
|
|
|
|
a2nxn |
b2 |
, |
|||
a21x1 a22x2 |
|||||||||
|
|
|
|
|
|
|
|
|
(1) |
, |
|
||||||||
|
|
|
|
|
|
|
|
|
|
a |
x a |
n2 |
x |
a |
nn |
x |
n |
b , |
|
|
n1 1 |
2 |
|
|
n |
|
|||
называемой системой n линейных алгебраических уравнений (СЛАУ) с n
неизвестными.
При этом произвольные числа aij (i = 1, 2,…, n; j = 1, 2,…, n) называются
коэффициентами при неизвестных, а числа bi (i = 1, 2,…, n) – свободными
членами.
Систему(1) можно записать в матричной форме
A X = B,
где A – матрица коэффициентов при неизвестных:
|
a |
a |
|
a |
|
|
|
|
11 |
12 |
|
1n |
|
A |
a21 |
a22 |
|
a2n |
||
|
|
|
|
|
, |
|
|
|
|
||||
|
|
|
an1 |
an1 |
|
|
|
an1 |
an1 |
||||
X – вектор-столбец неизвестных X = (x1, x2, …, xn)T:
|
x |
|
|
|
|
1 |
|
X |
x2 |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
xn |
|
|
B – вектор-столбец свободных членов:
b1
b2 B ,
bn
или B = (b1,b2,..., bn)T.
(2)
(3)
(4)
(5)
1
2.Операции с матрицами в Excel
ВExcel для операций с матрицами служат функции из категории «Математические»:
1) МОПРЕД(матрица) – вычисление определителя матрицы, 2) МОБР(матрица) – вычисление обратной матрицы, 3) МУМНОЖ(матрица1;матрица2) – произведение матриц, 4) ТРАНСП(матрица) – транспонирование матрицы.
Первая из этих функций в качестве результата возвращает число (определитель матрицы), поэтомувводится как обычная формула (ENTER).
Последние три возвращают блок ячеек, поэтому должны вводиться как формулы массива (CTRL+SHIFT+ENTER).
Рассмотрим задачурешения СЛАУ на следующем примере
8x1 2x2 8x3 24,
2x1 2x2 10x3 48,
2x1 4x2 8x3 18.
Матрица коэффициентов при неизвестных A (3) имеет вид
8 |
2 |
8 |
|
|
|
|
2 |
|
|
A 2 |
10 , |
|||
|
2 |
4 |
8 |
|
|
|
|||
а вектор-столбец свободных членов (5) B = (–24, –48, 18)T.
Решим СЛАУ (7) в среде MS Excel тремя различными способами.
Матричный способ решения (обратной матрицы)
(7)
(8)
Обе части матричного равенства (2) умножим на обратную матрицу А-1. Получим A–1 A X=A–1 B. Так как A–1 A=E, где E – единичная матрица (диагональная матрица, у которой по главной диагонали расположены единицы). Тогда решение системы (2) запишется в следующем виде
X = A-1 B. |
(11) |
Для решения необходимо найти для матрицы A (3) обратную A-1 и умножить
еена вектор-столбец B (5) свободных членов, последовательно
воспользовавшись |
функциями |
Excel |
МОБР(матрица) |
и |
2
МУМНОЖ(матрица1;матрица2), завершая в каждом случае ввод комбинацией
CTRL+SHIFT+ENTER.
Метод Крамера
Решение СЛАУ находится по формулам Крамера
|
det A |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
det A |
|
||||
|
|
|
|
|
|
|
|
det A2 |
|
|
|
|
|
X |
|
|
|
|
, |
(9) |
det A |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
det A |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||
|
det A |
|
|
|
|
|
где det A = A – определитель матрицы (3) системы (главный определитель), det Ai = Ai (i = 1, 2, …, n)– определители матриц Ai (вспомогательные определители), которые получаются из A заменой i-го столбца на столбец свободных членов B (5).
Для рассматриваемой СЛАУ (7) вспомогательные матрицы имеют следующий вид
24 2 |
8 |
8 |
24 |
8 |
8 |
2 |
24 |
|
|||||||
|
|
2 |
10 |
|
|
|
48 |
10 |
|
|
|
2 |
48 |
|
(10) |
A1 48 |
, A2 |
2 |
, A3 |
2 |
. |
||||||||||
|
18 |
4 |
8 |
|
|
2 18 |
8 |
|
|
2 |
4 |
18 |
|
|
|
|
|
|
|
|
|
|
|||||||||
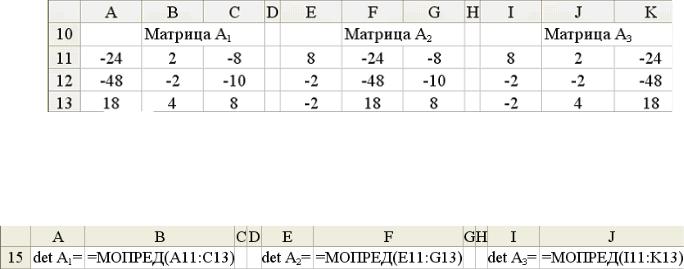
Разместим их на рабочем листе (рис. 1).
Рис. 1
Далее, воспользовавшись функцией МОПРЕД(матрица), вычислим определители всех матриц (рис. 2).
3

Рис. 2
Аналогичная формула (=МОПРЕД(A3:C5)) для вычисления определителя матрицы A записана в ячейку E8. Осталось найти решение системы. Соответствующие формулы Excel запишем в интервал решения B7:B9 (рис. 3), в котором и увидим результат (рис. 4).
Обратите внимание на то (рис. 3), что при вычислении xi (i = 1, 2, 3)
анализируется значение определителя матрицы системы A, вычисленное в ячейке E8, и, если оно равно нулю, то в B7 помещается текст «Решения нет», а в ячейки B8 и B9 – пустые строки.
Рис. 3
Рис. 4
3. Решение СЛАУ с использованием инструмента Поиск решения
Широкий класс производственных задач составляют задачи оптимизации. Задачи оптимизации предполагают поиск значений аргументов, доставляющих функции, которую называют целевой, минимальное или максимальное значение при наличии каких-либо дополнительных ограничений. Excel располагает мощным средством для решения оптимизационных задач.
4
Это инструмент-надстройка, который называется Поиск решения (Solver)
(доступен через меню Сервис Поиск решения).
Задачу решения СЛАУ можно свести к оптимизационной задаче.
Для чего одно из уравнений (например, первое) взять в качестве целевой функции, а оставшиеся n-1 рассматривать в качестве ограничений.
Запишем систему(1) в виде
a11x1 a12x2 a1nxn b1 0,
|
|
|
|
a2nxn |
b2 |
0, |
||
a21x1 a22x2 |
||||||||
|
|
|
|
|
|
|
|
(12) |
, |
|
|||||||
|
|
|
|
|
|
|
|
|
a |
x a |
n2 |
x |
a |
nn |
x |
b 0. |
|
|
n1 1 |
2 |
|
n |
n |
|
||
Для решения этой задачи необходимо записать выражения (формулы) для вычисления значений функций, стоящих слева в уравнениях системы (12). Отведем для примера под эти формулы интервал C7:C9. В ячейку C7 введем формулу =A3*$B$7+B3*$B$8+C3*$B$9-D3 и скопируем ее в оставшиеся C8 и C9. В них появятся соответственно =A4*$B$7+B4*$B$8+C4*$B$9-D4 и =A5*$B$7+B5*$B$8+C5*$B$9-D5.
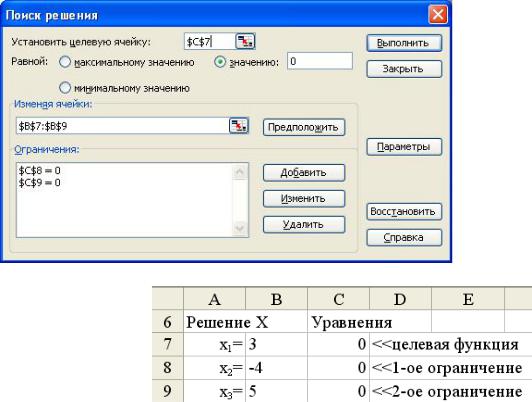
В окне диалога Поиск решения (рис. 5) задать параметры поиска (установить целевую ячейку C7 равной нулю, решение в изменяемых ячейках B7:B9, ограничения заданы формулами в ячейках C8 и С9). После щелчка по кнопке Выполнить в
интервале B7:B9 получим результат (рис. 6) – решение СЛАУ.
Рис. 5
Рис. 6
5
