МАТЕМАТИКА ZIP File / Лек бак 2 семестр / Теоремыа

9

Предельные теоремы теории вероятности

Пусть взаимно независимые, одинаково распределенные случайные величины с параметрами:

Случайная величина , которую называют средним арифметическим, имеет характеристики:

;

;

.

Вводим нормированную и центрированную случайную величину

.

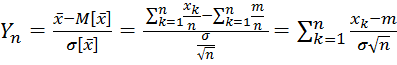Случайная величина имеет характеристики:

;

;

Поскольку .

Характеристическая функция имеет вид:

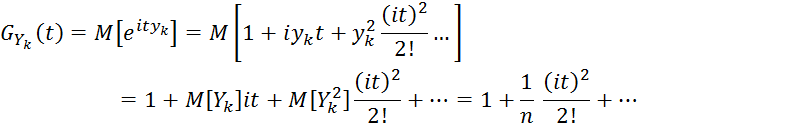
Характеристическая функцию суммы является произведением:

.

Центральная предельная теорема

Если случайные величины независимы и одинаково распределены, а также имеют конечные математическое ожидание и дисперсию:

=;

Тогда для любого действительного закон распределения нормированного и центрированного среднего арифметического случайных величин при стремится к нормальному закону распределения с параметрами и :

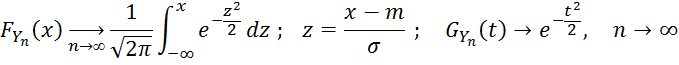
Действительно, ранее получили, что характеристическая функция нормированного и центрированного среднего арифметического имеет вид

.

При получаем неопределенность , которую раскрываем, используя основное логарифмическое тождество и разложение в ряд логарифмической функции

.

.

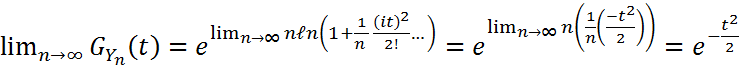Таким образом, нормальное распределение является предельной формой распределения суммы большого числа случайных величин, из которых ни одна не доминирует над другой.

Следствия центральной предельной теоремы

Теоремы Муавра – Лапласа.

Рассматриваем биномиальное распределение (схема Бернулли): вероятность того, что при испытаниях событие появится раз:

;

В случае ; ; это распределение приближенно заменяют распределением Пуассона

.

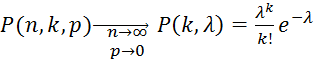При достаточно больших значениях биномиальное распределение приближенно заменяют нормальным распределением.

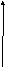
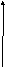
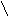
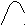
С учетом того, что и вводя

, получаем:

1. Вероятность того, что при 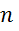испытаниях событие 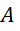появится 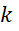раз:

; (Локальная теорема Муавра –Лапласа)

2. Вероятность того, что при истытаниях событие 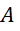происходит 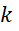раз при условии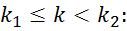

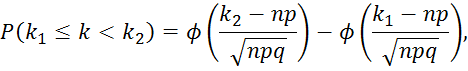
где значения функции плотности вероятности и интегральной функции распределения находим по таблицам (Интегральная теорема Муавра-Лапласа).

Закон больших чисел в форме Бернулли

Пусть - число испытаний Бернулли, а – относительная частота события Найдем вероятность того, что относительная частота события отличается от его вероятности не более, чем на

С учётом того, что 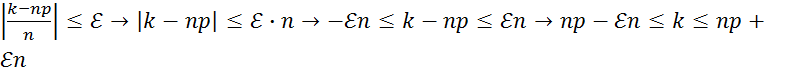и, используя интегральную теорему Муавра-Лапласа, получаем:

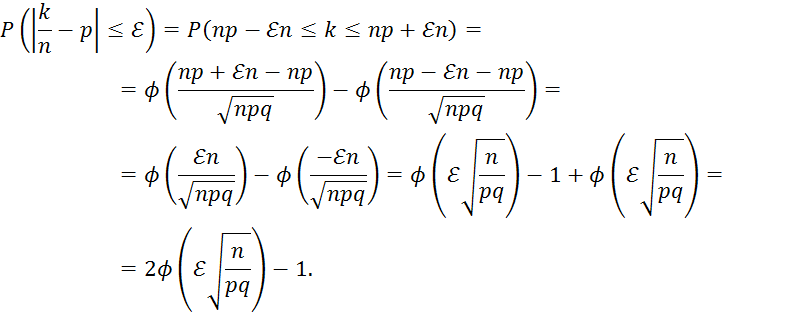
Здесь использовали свойство 𝜙

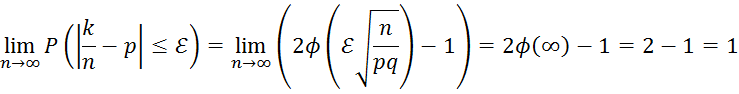
Относительная частота события (“успех”) в независимых испытаниях при стремится к вероятности одного испытания. Или относительная частота сходится по вероятности к вероятности одного испытания.

В статистике относительная частота события является оценкой вероятности события.

Неравенство Чебышева

0

ε

-ε

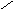
На рис. представлена функция плотности вероятности с математическим ожиданием

В этом случае дисперсия совпадает со вторым начальным моментом:

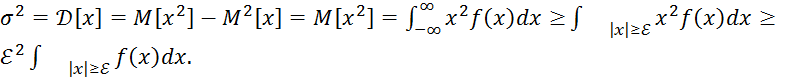Неравенство следует из того, что площадь под графиком равна 1 и она больше, чем площадь под “ хвостами ” распределений.

С учётом того, что , получаем

.

Теорема Чебышева

Пусть … взаимно независимые и одинаково распределенные случайные величины с параметрами

- среднее арифметическое .

С учётом того, что для случайной величины

отклонение среднего от получаем

.

Записывая для этой случайной величины неравенство Чебышева:

Последовательность средних арифметических случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.

В статистике выборочное среднее является несмещенной и состоятельной оценкой математического ожидания.