
3341
.pdfФедеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
šКузбасский государственный технический университетŸ
Кафедра физики
I . К И Н Е М А Т И К А
Методические указания для самостоятельной работы по решению индивидуальных задач и задания для самоконтроля
по разделу общей физики для студентов всех специальностей
Составители Т. В. Лавряшина Н. Б. Окушко И. В. Цвеклинская
Утверждены на заседании кафедры Протокол № 3 от 11.10.2007
Рекомендованы к печати учебно-методической комиссией специальности 130404 Протокол № 17 от 06.11.2007
Электронная копия находится в библиотеке главного корпуса ГУ КузГТУ
Кемерово 2007
1
Самостоятельная работа студентов осуществляется за счет времени, предусмотренного рабочей программой и ГОСом на изучение физики, и составляет примерно 50% от общего числа отведенных часов. Результаты самостоятельной работы проверяются преподавателем на консультациях, при проведении контрольных работ и приеме индивидуальных заданий на практических занятиях, при собеседовании во время выполнения работ лабораторного практикума, при тестовом контроле в процессе изучения курса и тестовом контроле остаточных знаний.
Контроль качества усвоения полученных знаний по кинематике поступательного и вращательного движения проводится в процессе обсуждения соответствующих вопросов как в динамике поступательного и вращательного движения, так и в других разделах курса физики (гармонические колебания, движение заряженных частиц в электромагнитном поле и т. д.). При этом проверяется знание основных понятий, определений и формул кинематики:
1)материальная точка и твердое тело;
2)система отсчета, система координат;
3)радиус-вектор, его выражение через координаты х , у , z
(прямоугольная система координат);
4)вектор перемещения и пройденный путь;
5)средняя и мгновенная скорость;
6)среднее и мгновенное ускорение;
7)кинематические уравнения поступательного движения;
8)угловая скорость и угловое ускорение;
9)кинематические уравнения вращательного движения;
10)связь линейных и угловых характеристик при вращательном движении.
Студент, успешно выполняющий самостоятельную работу, имеет возможность получить высокую рейтинговую оценку по физике, и, следовательно, своевременно получить зачет и высокую экзаменационную оценку.
2
При изучении курса физики в вузе большое значение имеет практическое применение теоретических знаний, главное из которых – умение самостоятельно решать задачи.
Выработка приемов и навыков решения конкретных задач из разных областей физики помогает в дальнейшем решать и сложные инженерные задачи.
1 . О Б Щ И Е П Р А В И Л А П Р И Р Е Ш Е Н И И З А Д А Ч
Не приступайте к решению задач, не проработав теоретический материал на соответствующую тему.
Прежде чем приступить к решению той или иной задачи, необходимо хорошо понять ее содержание и поставленные вопросы.
1 .1 . Примерная схема решения задач
При решении задач целесообразно придерживаться следующей схемы:
1)по условию задачи представьте себе физическое явление, о котором идет речь. Сделайте краткую запись условия, выразив исходные данные в единицах СИ;
2)сделайте, где это необходимо, чертеж, схему или рисунок, поясняющий описанный в задаче процесс;
3)напишите уравнения или систему уравнений, отображающие физический процесс;
4)используя чертежи и условие задачи, преобразуйте уравнения так, чтобы в них входили лишь исходные данные и табличные величины;
5)решив задачу в общем виде, проверьте ответ по равенству размерностей величин, входящих в расчетную формулу;
6)осуществите вычисления и, получив числовой ответ, оцените его реальность.
3
2 . К И Н Е М А Т И К А П О С Т У П А Т Е Л Ь Н О Г О И В Р А Щ А Т Е Л Ь Н О Г О Д В И ЖЕ Н И Я
Решая задачи по кинематике, в которых необходимо использовать математический аппарат дифференциального и интегрального исчисления, студент должен научиться определять мгновенные скорость и ускорение по заданному уравнению движения (прямая задача) и уметь составлять уравнение движения по известным зависимостям скорости или ускорения от времени (обратная задача).
В задачах на кинематику вращательного движения твердого тела главное внимание уделяется изучению соотношений между линейными и угловыми характеристиками.
2 . 1 . О с н о в н ы е п о н я т и я и ф о р м у л ы
ки н е м а ти к и
Вприведенных ниже основных положениях кинематики курсивом выделены определения и формулы, необходимые для решения задач и подготовки к экзамену.
Физическая система может состоять из одного идеального объекта – материальной точки (тело, размерами которого в данной задаче можно пренебречь) или содержать большое число элементов, положение которых в процессе движения не изменяется (твердое тело).
|
|
|
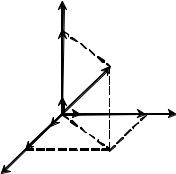
Положение материальной точки в |
|||
Y |
|
|
пространстве определяют ее координа- |
|||
yj |
|
|
тами (например, координаты x, y, z в де- |
|||
|
|
|
картовой системе координат) или задают |
|||
r |
|
радиус-вектор |
r |
этой точки (рис. 2.1). |
||
j |
||||||
О |
i |
xi |
Радиус-вектор точки – это вектор, |
|||
|
X |
проведенный |
из |
начала координат в |
||
zk |
k |
|
данную точку. |
|
|
|
|
|
|
|
|
||
Z |
|
|
Как видно из рис. 2.1, проекции ра- |
|||
Рис. 2.1 |
|
диуса-вектора на оси X, Y, Z – это коор- |
||||
|
динаты данной точки. Поэтому радиус- |
|||||
вектор можно представить в виде

4
r xi yj zk ,
где i , j , k – единичные векторы (орты), направленные, соответственно, вдоль осей X, Y, Z.
Движение материальной точки можно описать при помощи векторного уравнения
|
r r (t) |
|
(2.1) |
или тремя скалярными уравнениями: |
|
|
|
x x(t) , |
y y(t) , |
z z(t) , |
(2.2) |
которые называют кинематическими уравнениями движения. Вектор перемещения или просто перемещение материальной
точки за время t t2 t1 |
– это вектор r , проведенный из поло- |
||
Y |
S |
|
жения точки в момент времени t1 (на- |
|
чальное) в положение, в котором она |
||
t1 |
|
t |
находится в момент времени t2 (конеч- |
|
r |
2 |
|
r1 |
|
|
ное). Как видно из рис. 2.2, перемеще- |
О |
r2 |
|
ние равно приращению радиуса- |
|
|
вектора за рассматриваемый промежу- |
|
Xток времени:
Z r r2 r1. (2.3)
Рис. 2.2 |
Необходимо различать вектор пе- |
|
|
|
ремещения и пройденный путь. Путь S |
– это скалярная величина, равная расстоянию, пройденному по траектории за указанный промежуток времени.
Вектором средней скорости |
|
|
называется отношение пе- |
||
|
|
||||
ремещения r |
к промежутку времени t |
||||
|
|
r |
|
|
|
|
|
|
|
. |
(2.4) |
|
t |
||||
|
|
|
|
||
Направления вектора средней скорости и вектора перемещения совпадают.
Мгновенная скорость (скорость) равна первой производной радиус-вектора по времени

|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
r |
|
dr |
|
dx |
dy |
dz |
|
|||
lim |
|
lim |
|
|
|
|
|
i |
|
j |
|
k . |
(2.5) |
|
dt |
|
|
|
|||||||||
t 0 |
|
t 0 t |
|
|
dt |
dt |
dt |
|
|||||
Вектор мгновенной скорости направлен по касательной к траектории (рис. 2.3). Если t 0 и r dS , то модуль вектора
скорости |
|
|
|
a |
|
|
|
|
a |
an |
|
Рис. 2.3
|
dS |
. |
(2.6) |
|
|||
|
dt |
|
|
Из уравнения (2.5) видно, что проекции вектора скорости на координатные оси X, Y, Z равны:
x |
dx |
; |
y |
dy |
; |
z |
dz |
, (2.7) |
|
|
|
||||||
|
dt |
|
dt |
|
dt |
|||
модуль вектора скорости определяется соотношением
|
|
|
|
dx 2 |
||
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
dt |
||
|
|
|
|
|||
dy 2 |
dz |
2 |
|
|
|||||
2x 2y 2z . (2.8) |
|||||||||
|
|
|
|
|
|
|
|||
|
|
||||||||
dt |
dt |
|
|
|
|||||
Из уравнений (2.5)–(2.7) получаем кинематические уравнения движения материальной точки:
|
|
|
t |
|
(2.9) |
|
r |
(t) r (0) dt |
|||
|
|
|
0 |
|
|
или в проекциях на координатные оси |
|
|
|
||
t |
|
t |
|
t |
|
x(t) x(0) xdt ; |
y(t) y(0) ydt ; |
z(t) z(0) zdt ; |
(2.10) |
||
0 |
|
0 |
|
0 |
|
а путь, пройденный материальной точкой за время t , |
|
||||
|
|
t |
|
|
|
|
|
S (t) dt . |
|
(2.11) |
|
|
|
0 |
|
|
|
Ускорением точки называется вектор а , равный производной вектора скорости этой точки по времени

|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
d |
|
|
|
|
d y |
|
|
d |
|
|
|
||||||||
|
d |
х |
|
|
|
z |
|
|||||||||||||||
а |
|
|
|
|
|
|
i |
|
|
|
|
j |
|
|
|
k . |
(2.12) |
|||||
|
|
|
|
|
dt |
|
|
|
|
|||||||||||||
|
|
dt |
dt |
|
|
|
|
|
dt |
|
|
|
||||||||||
Проекции вектора ускорения на координатные оси X, Y, Z: |
||||||||||||||||||||||
аx |
d |
x |
; |
аy |
|
d y |
|
; |
аz |
d |
z |
; |
(2.13) |
|||||||||
|
|
|
|
dt |
|
|
|
|
||||||||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
dt |
|
|||||||||
и модуль вектора ускорения через его проекции записывается в виде
а 
 аx2 а2y аz2 . (2.14)
аx2 а2y аz2 . (2.14)
Из уравнений (2.12), (2.13) можно выразить зависимость вектора скорости и его компонент от времени:
|
|
|
t |
|
(2.15) |
|
(t) (0) а(t)dt ; |
||||
|
|
|
0 |
|
|
t |
|
|
|
t |
t |
x (t) x (0) axdt ; |
y (t) y (0) ay dt ; |
z (t) z (0) az dt . |
|||
0 |
|
|
|
0 |
0 |
|
|
|
|
|
(2.16) |
В некоторых случаях удобнее разложить вектор ускорения на две составляющие, одна из которых параллельна или антипарал-
лельна скорости ( а ), а другая – перпендикулярна скорости ( аn ) (см. рис. 2.3). Вектор а называют тангенциальным ускорением, его модуль характеризует изменение скорости по величине:
а |
d |
. |
(2.17) |
|
|||
|
dt |
|
|
Вектор аn называют нормальным ускорением, он характеризует изменение скорости по направлению. При движении тела по окружности радиуса R нормальное ускорение направлено к центру и выражается формулой
|
2 |
|
|
аn |
|
. |
(2.18) |
|
|||
|
R |
|
|

7
Любую другую траекторию вблизи произвольной точки можно считать сколь угодно близкой к окружности, следовательно, радиус R кривизны траектории в данной точке можно найти из формулы (2.18):
R |
2 |
|
|||
|
. |
|
(2.19) |
||
|
|||||
|
|
аn |
|
||
Вектор полного ускорения определяется векторной суммой |
|||||
нормального и тангенциального ускорения |
|
||||
|
a , |
(2.20) |
|||
а аn |
|||||
а его модуль равен |
|
|
|
|
|
a |
|
|
. |
|
|
an2 |
a2 |
(2.21) |
|||
Движение тела с постоянным по величине и направлению ускорением называется равноускоренным. В случае равноускоренного движения его уравнение имеет вид
|
|
|
|
2 |
|
|
аt |
(2.22) |
|||||
r |
r0 |
0t |
|
|
||
2 |
||||||
|
|
|
|
|||
или в проекциях на координатные оси:
x x |
|
0 x |
t |
аxt 2 |
; |
(2.23) |
||||
|
|
|||||||||
0 |
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
||||
y y0 |
0 yt |
|
аyt 2 |
|
; |
(2.24) |
||||
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
|||
z z0 |
0 zt |
аzt 2 |
. |
(2.25) |
||||||
|
||||||||||
|
|
|
2 |
|
|
|
|
|||
В уравнениях (2.22)–(2.25) r0 – радиус-вектор, описывающий начальное положение точки; 0 – вектор начальной скорости; x0 , y0 , z0 – начальные координаты; 0 x , 0 y , 0 z – проекции вектора
начальной скорости на оси X, Y, Z.
В частном случае a 0 движение является равномерным.

8
Для описания вращения твердого тела относительно неподвижной оси используются понятия угла поворота d (псевдовектор), угловой скорости и углового ускорения . Угловой скоростью называется вектор, величина которого равна производной угла поворота по времени
d
d
Рис. 2.4
|
d |
. |
(2.26) |
|
|||
|
dt |
|
|
Вектор угловой скорости направлен вдоль оси вращения, его направление связано c направлением вращения и определяется правилом šбуравчикаŸ (рис. 2.4).
Производная вектора угловой скорости по времени называется угловым ускорением :
|
d |
|
|
|
|
|
|
. |
(2.27) |
|
|
|||
dt
При ускоренном вращении материальной точки или твердого тела вокруг неподвижной оси направления векторов углового ускорения и угловой скорости совпадают, при замедленном они направлены противоположно.
Как и в случае поступательного движения, из уравнений (2.26), (2.27) можно найти угловую скорость и угол поворота:
|
t |
|
|
|
|
t |
|
|
|
(t) (0) (t)dt ; |
(t) (0) (t)dt . |
(2.28) |
|||||||
|
0 |
|
|
|
|
0 |
|
|
|
Равноускоренное вращение описывается уравнениями: |
|
||||||||
const ; |
|
t ; |
|
0 |
t |
t 2 |
, |
(2.29) |
|
|
|||||||||
|
0 |
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где 0 – начальный угол поворота; 0 – начальная угловая скорость; – угловое ускорение (не зависящее от времени).
При вращении точки относительно фиксированной оси ее линейные и угловые характеристики связаны между собой соот-
ношениями: |
|
R ; |
(2.30) |

9 |
|
a R ; |
(2.31) |
an 2 R , |
(2.32) |
где R – расстояние от точки до оси вращения (радиус вращения).
2 . 2 . П р и м е р ы р е ш е н и я з а д а ч
Ниже в качестве примера приведены задачи по кинематике. Ознакомившись с их решением, студенты могут перейти к решению задач для индивидуальной подготовки и после самостоятельного решения задач, приведенных в задании, подготовиться к контрольной работе на эту тему. Ответы на качественные вопросы помогут студентам глубже понять протекающие физические процессы, подготовиться к практическим занятиям и выполнению работ лабораторного практикума по теме šКинематикаŸ с последующим обсуждением результатов эксперимента.
Пример 1. Кинематическое уравнение движения точки по прямой (ось X ) имеет вид x A Bt Ct3, где A 4 м , В 2 м/с ,
С 0,5 м/с3. Для момента t 2 c определить координату точки x , мгновенные скорость x и ускорение ах . Определить среднюю
скорость |
х |
за первые две секунды t 2 c движения и среднее |
ускорение |
ах |
за это время. |
Решение. Необходимо определить параметры движения по кинематическому уравнению (прямая задача кинематики). Она решается последовательным применением уравнений (2.23; 2.7; 2.13; 2.4). Подставляя в уравнение движения t 2 c, получаем координату в указанный момент времени
x A Bt Ct3 (4 2 2 0,5 23 ) 4 м .
Мгновенная скорость точки в этот момент равна
x dx B 3Ct 2 2 3 ( 0,5) 22 4 м/с . dt
