Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Сопротивление материалов.pdf
202
что значительно ниже допускаемого, поэтому выполним второе приближение
j = 0,5 + 0,804 = 0,65, 2
|
Р |
240 ×103 |
2 мм2 = 23 см2. |
|
F ³ |
|
= |
0,65 ×160 = 23×10 |
|
j[s] |
||||
Этой площади соответствует сечение из двух уголков ∟ 75×75×8 с геометрическими характеристиками:
F = 2 ×11,5 = 23 см2 , imin = i x = 2,28 cм,
l = |
m |
= |
0,7 × 2,8 ×103 |
= 85,5 ® j = 0,717. |
|
imin |
22,8 |
||||
|
|
|
Допускаемое напряжение
[sy ]= j[s]= 0,717 ×160 = 114,7 Н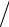
мм2 .
Расчетное напряжение
s = |
Р |
= |
240 ×103 |
= 104,4 Н мм2 . |
|
F |
23×102 |
||||
|
|
|
Недогруз составит
d = 114,7 −104,4100 % = 9 %. 114,7
Уровень недогруза достаточно велик, поэтому проведем расчет по третьему приближению
j = 0,65 + 0,717 = 0,683. 2
|
Р |
240 × |
103 |
|
2 мм2. |
|
F ³ |
|
= |
|
|
= 22 ×10 |
|
j[s] |
0,683 |
×160 |
||||