151
Конструкция рамы состоит из одного диска, на который наложено пять связей. Степень статической неопределимости заданной конструкции k = m – n = 5 – 3 = 2.
Система канонических уравнений в имеет вид
δ11 X1 + δ12 X2 + 1p = 0,
d21 X1 + d22 X2 + D2p = 0.
Определение единичных и грузовых перемещений выполним с помощью правила Верещагина
|
|
|
|
|
|
|
|
|
|
1 Mp ds |
|
|
|
1 |
|
éæ |
|
|
320 × 4 öæ |
1 |
|
|
|
|
2 |
|
|
|
1 |
|
|
320 × 6 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
ö |
|
æ |
|
ö |
|
|
|
||||||||||||||||||||||
D1p |
= |
å ò |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
êç |
- |
|
|
|
֍ |
|
4 + |
|
|
8 |
÷ + |
|
ç |
- |
|
|
|
÷ |
8 |
+ |
|
||||||||||
|
|
|
|
|
|
EJ |
|
|
|
EJ0 |
|
|
2 |
3 |
3 |
2 |
2 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ëè |
|
|
|
|
øè |
|
|
|
|
|
ø |
|
è |
|
|
|
ø |
|
|
|
|||||||||||
|
1 |
æ |
|
500 × 6 ö |
|
1 |
æ |
10 × 63 ö |
|
|
|
æ |
|
480 ×8 |
öæ |
|
2 |
|
ö |
|
æ |
160 ×8 öæ |
1 |
|
öù |
|
|
|||||||||||||||||||||
+ |
|
ç- |
|
|
|
|
|
|
|
|
÷8 + |
|
ç |
|
|
|
|
|
÷ |
8 |
|
+ ç |
- |
|
|
֍ |
|
|
|
8÷ |
+ |
ç |
|
|
|
֍ |
|
8÷ú = |
||||||||||
2 |
|
2 |
|
|
2 |
ç |
|
|
12 |
|
÷ |
|
2 |
|
|
3 |
|
2 |
3 |
|||||||||||||||||||||||||||||
|
è |
|
|
|
|
ø |
|
è |
|
|
|
ø |
|
|
|
è |
|
|
øè |
|
|
ø è |
|
øè |
|
øû |
|
|
||||||||||||||||||||
= - |
21930 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
EJ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 Mp |
|
|
|
|
1 |
|
é1 |
|
|
320 × 6 |
|
1 |
|
|
|
|
1 |
|
|
500 × 6 |
|
2 |
|
|
|
|||||||||||||
D2p |
|
= |
å |
|
|
M |
ds = |
|
æ |
- |
öæ |
6 |
ö |
+ |
æ |
- |
öæ |
6 |
ö |
+ |
||||||||||||||||||||||||||||
|
ò |
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
ç |
|
|
֍ |
|
÷ |
|
ç |
|
|
|
֍ |
|
÷ |
|||||||||||||||||||
|
|
|
|
|
|
|
EJ |
|
|
EJ0 |
|
|
|
2 |
3 |
2 |
|
|
2 |
3 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë2 |
è |
|
|
øè |
|
|
ø |
|
è |
|
|
|
øè |
|
ø |
|
||||||||||||||
|
1 |
æ |
10 × |
6 |
3 |
ö |
æ 6 ö |
|
æ |
|
|
480 ×8 ö |
|
|
|
æ160 ×8 ö |
|
ù |
|
|
|
|
11460 |
|
|
|
|
|
|
|
|
|||||||||||||||||
+ |
ç |
|
|
|
÷ |
|
- |
|
|
|
|
= - |
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2 |
ç |
|
12 |
|
|
|
|
÷ |
ç ÷ |
+ ç |
|
2 |
|
÷6 + |
ç |
2 |
÷ |
6ú |
EJ0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
è |
|
|
|
|
|
ø |
è 3 ø è |
|
|
|
|
ø |
|
|
|
è |
ø |
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
152
|
а) Заданная система |
|
||
|
|
q = 10 кН/м |
|
|
2 |
|
|
3 |
4 |
|
|
2EJ0 |
||
Р =80 кН |
|
4 м |
||
|
|
|
||
|
1 |
|
EJ0 |
|
|
|
|
||
|
|
|
|
4 м |
А |
|
|
В |
|
A |
|
6 м |
|
|
|
|
2 м |
||
|
|
|
||
г) |
Грузовое состояние |
|||
q
Р
д) Единичные состояния
X1 = 1
8
8
M1
б) Основная система в) Эквивалентная система
Р
X1 |
|
X1 |
X2 |
|
X2 |
320 500
20
480
Mp
160
X2 =1
6
6
M2
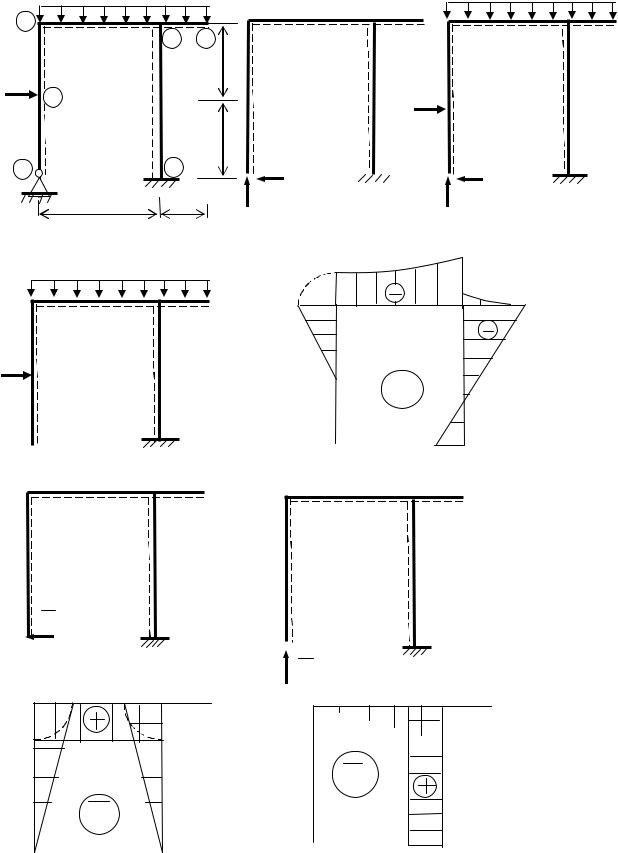
Рис. 6.17. Расчет статически неопределимой рамы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
153 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2ds |
|
|
1 |
|
|
é 8 ×8 |
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
8 ×8 |
|
|
2 |
|
|
ù |
|
533 |
|
||||||||||||
|
|
M |
|
|
öæ |
|
|
ö |
|
|
|
|
|
|
|
æ |
öæ |
|
ö |
|
|
|||||||||||||||||||||||||
d11 |
= å ò |
1 |
|
|
= |
|
|
|
|
|
|
æ |
|
|
|
|
8 |
|
+ |
|
|
(8 × 6)8 + |
|
|
|
|
8 |
|
|
= |
|
; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
êç |
|
|
|
֍ |
|
÷ |
|
|
|
ç |
|
|
|
֍ |
|
÷ú |
|
|||||||||||||||||
|
EJ |
|
|
EJ0 |
|
2 |
3 |
|
2 |
|
2 |
|
3 |
EJ0 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ëè |
|
øè |
|
|
ø |
|
|
|
|
|
|
|
è |
|
|
øè |
|
øû |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
2ds |
|
|
1 |
é1 |
æ |
6 × 6 |
ö |
æ |
8 ×8 |
ö |
ù |
|
|
264 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
M |
M |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
d12 = d21 = å |
ò |
|
|
|
|
|
|
|
|
|
= |
|
|
ê |
|
|
ç |
|
|
|
|
|
÷8 |
+ ç |
|
|
|
÷6ú |
|
= |
|
|
|
|
. |
|
|
|
||||||||
|
|
|
|
EJ |
|
EJ0 |
2 |
|
|
2 |
|
2 |
|
|
EJ |
0 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
è |
|
|
|
ø |
è |
|
ø |
û |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
22ds |
|
|
1 |
|
|
é1 |
æ |
6 × 6 |
öæ |
2 |
|
|
ö |
|
|
|
|
ù |
|
|
324 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
d22 |
= å ò |
|
|
|
|
|
|
= |
|
|
|
|
|
ê |
|
ç |
|
|
֍ |
|
|
6 |
÷ |
+ |
(6 |
×8)6ú |
= |
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||
|
EJ |
|
|
EJ0 |
|
2 |
3 |
EJ0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ë2 |
è |
øè |
|
|
ø |
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Окончательный вид канонических уравнений и значения реакций лишних связей:
533 X1 + |
264 X2 |
- |
21930 = 0; |
|
EJ0 |
|
EJ0 |
|
EJ0 |
264 X1 + |
324 X2 |
- |
11460 = 0; |
|
EJ0 |
EJ0 |
|
EJ0 |
|
X1 |
= 39,6 кН; |
|
|
|
X2 |
= 3,1 кН; |
|
|
|
Определим значения изгибающих моментов по формуле (6.22):
MA = 0; M1 = 0 + 4×39,6 + 0 =158,4 кН×м; М2 = -320 +8×39,6 + 0 = – 3,2 кН×м; М32 = -500 + 8×39,6 +6×3,1 = – 164,6 кН×м; М34 = – 20 кН×м;
М3В = – 480 +8×39,6+ 6×3,1 = –144,6 кН×м; МВ = 160 + 0 +6×3,1 = 178,6 кН×м.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
154 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Проверим определение M путем перемножения его эпюры на од- |
||||||||||||||||||||||||||||||||||||||||
ну из единичных эпюр, например |
|
1. Так как перемещение |
|
1 в на- |
||||||||||||||||||||||||||||||||||||||||
M |
|
|||||||||||||||||||||||||||||||||||||||||||
правлении связи 1 равно нулю, то: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
D1 |
= å ò |
|
|
M1 |
M |
ds = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
(L) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
éæ158,4 × 4 |
öæ 2 |
ö |
æ |
158,4 × 4 |
öæ |
2 |
|
|
|
1 |
ö |
|
æ |
3,2 × 4 öæ |
1 |
|
|
2 |
ö |
|||||||||||||||||||
D |
1 |
= |
|
|
|
|
ç |
|
|
|
|
|
|
|
֍ |
|
4÷ + |
ç |
|
|
|
|
|
֍ |
|
4 |
+ |
|
8÷ |
+ ç- |
|
֍ |
|
|
4 + |
|
8÷ + |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
EJ |
ê |
|
|
|
2 |
|
|
øè 3 |
ø è |
|
2 |
|
|
|
øè 3 |
|
|
|
3 |
ø è |
2 |
øè 3 |
|
|
3 |
ø |
|||||||||||||||
|
|
|
|
0 ëè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
+ |
1 æ |
- |
3,2 × 6 |
ö |
8 |
|
+ |
1 |
æ |
- |
164,6 × 6 |
ö |
+ |
1 |
æ10 × 63 |
ö |
|
|
æ |
- |
144,6 ×8 |
öæ 2 |
8 |
ö |
+ |
|
|
|||||||||||||||||
|
ç |
|
|
|
÷ |
|
|
ç |
|
|
|
|
÷8 |
|
ç |
|
|
|
|
|
÷ |
8 + ç |
|
|
֍ |
|
÷ |
|
|
|||||||||||||||
|
2 è |
|
|
|
2 |
ø |
|
|
|
|
2 |
è |
|
|
|
|
2 |
|
ø |
|
2 |
ç |
|
12 |
|
÷ |
|
|
è |
|
|
2 |
øè 3 |
|
ø |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
|
|
|
|||||||||||||||||||
+ |
æ |
178,6 ×8 öæ 1 |
|
öù |
= |
|
1 |
|
(5160 |
- 5140) |
= |
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ç |
|
|
|
|
֍ |
|
8÷ú |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2 |
3 |
EJ |
|
EJ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
è |
|
|
|
øè |
|
øû |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
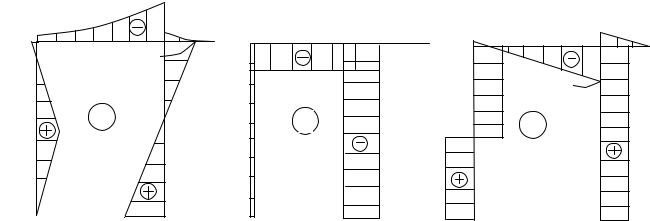
Этот результат практически равен нулю (с погрешностью менее 5%). Усилия Q и N в характерных сечениях находятся элементарно ме-
тодом сечений. Окончательные эпюры M, N и Q приведены на рис. 6.18.
3,2 |
164,6 |
|
3,1 |
20 |
|
|
|||
144,6 |
40,4 |
|
|
|
|
|
|
56,9 |
|
|
|
|
|
|
M |
|
N |
|
Q |
158,4 |
|
|
|
40,4 |
178,6 |
3,1 |
76,9 |
39,6 |
40,4 |
Рис. 6.18. Окончательные эпюры внутренних усилий
Статистическая проверка вырезанием узлов показана на рис. 6.19.