
Индивидуальные задания
«Технология транспортных процессов» бакалавры
(1-ый семестр)
4. Основы молекулярной физики и термодинамики
Идеальный газ. Столкновения молекул
 – количество вещества (число молей);
– количество вещества (число молей);
 ;
; – уравнение Менделеева-Клапейрона;
– уравнение Менделеева-Клапейрона;
 – концентрация молекул;
– концентрация молекул;
 – универсальная газовая постоянная;
– универсальная газовая постоянная;
 – закон Дальтона;
– закон Дальтона;
 – давление, оказываемое газом на стенки
сосуда;
– давление, оказываемое газом на стенки
сосуда;
 – средняя энергия поступательного
движения молекулы;
– средняя энергия поступательного
движения молекулы;
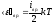 – средняя энергия вращательного движения
молекулы;
– средняя энергия вращательного движения
молекулы;
 – средняя кинетическая энергия молекулы
идеального газа;
– средняя кинетическая энергия молекулы
идеального газа;
 – внутренняя энергия идеального газа;
– внутренняя энергия идеального газа;
 – основное уравнение молекулярно-кинетической
теории для давления.
– основное уравнение молекулярно-кинетической
теории для давления.
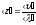 – среднее число столкновений молекулы
с другими молекулами в единицу времени;
– среднее число столкновений молекулы
с другими молекулами в единицу времени;
 – среднее время свободного пробега;
– среднее время свободного пробега;
 – средняя длина свободного пробега;
– средняя длина свободного пробега;
 эффективное сечение молекулы, где d
– эффективный диаметр молекулы.
эффективное сечение молекулы, где d
– эффективный диаметр молекулы.
Распределение молекул по скоростям. Барометрическая формула
 – функция распределения Максвелла
молекул по скоростям (доля молекул,
имеющих скорости в интервале от
– функция распределения Максвелла
молекул по скоростям (доля молекул,
имеющих скорости в интервале от
 до
до
 вблизи заданной скорости
вблизи заданной скорости
 ,
в расчете на единичный интервал
скоростей);
,
в расчете на единичный интервал
скоростей);
 ;
;
 ;
;
 – скорости молекул газа: средняя
квадратичная, средняя арифметическая,
наиболее вероятная;
– скорости молекул газа: средняя
квадратичная, средняя арифметическая,
наиболее вероятная;
 – распределение Больцмана, здесь n
и n0
– концентрации частиц в состояниях
с потенциальными энергиями
– распределение Больцмана, здесь n
и n0
– концентрации частиц в состояниях
с потенциальными энергиями
 и
и
 соответственно,
соответственно,
 ;
;
 ,
,
 –
барометрическая формула.
–
барометрическая формула.
Термодинамика. Теплоемкость. Изопроцессы
.
|
Процесс |
T=const Изотерма |
V=const Изохора |
p=const Изобара |
S=const Адиабата |
|
Уравнение процесса |
|
|
|
|
|
Первое начало термодинамики |
|
|
|
|
|
Работа |
|
0 |
|
|
|
Изменение внутренней энергии |
0 |
|
|
|
|
Количество теплоты |
|
|
|
0 |
|
Изменение энтропии |
|
|
|
0 |
 – первое начало термодинамики;
– первое начало термодинамики;
 ;
;
 – работа идеального газа;
– работа идеального газа;
 ;
;
 ;
;
 – теплоёмкость тела; удельная и молярная
теплоемкость;
– теплоёмкость тела; удельная и молярная
теплоемкость;
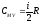 ;
;
 – молярные теплоемкости идеального
газа при постоянном объеме и при
постоянном давлении;
– молярные теплоемкости идеального
газа при постоянном объеме и при
постоянном давлении;
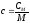 – связь удельной и молярной теплоемкостей.
– связь удельной и молярной теплоемкостей.
Круговой процесс (цикл). КПД цикла. Цикл Карно
 – КПД цикла;
– КПД цикла;
 – КПД цикла Карно.
– КПД цикла Карно.
Энтропия. Изменение энтропии
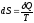 ;
;
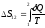 – определение энтропии (Клаузиус);
– определение энтропии (Клаузиус);
 – определение энтропии (Больцман);
– определение энтропии (Больцман);
где w – термодинамическая вероятность состояния системы (число микросостояний, которыми можно реализовать данное макросостояние).
Примеры решения задач
Задача 1
Найти среднее число всех соударений, которое происходит в течение 1 с между всеми молекулами в 4 мм3 водорода при нормальных условиях. Эффективный диаметр принять 0.23 нм.
 Решение
Решение
Если N – полное число
молекул, а
 – среднее число соударений в секунду
одной молекулы, то искомое полное число
соударений в секунду между всеми
молекулами равно:
– среднее число соударений в секунду
одной молекулы, то искомое полное число
соударений в секунду между всеми
молекулами равно:
 .
Коэффициент
.
Коэффициент
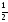 учитывает, что в каждом соударении
участвуют две молекулы. Средняя
арифметическая скорость молекул
учитывает, что в каждом соударении
участвуют две молекулы. Средняя
арифметическая скорость молекул
 ,
а средняя длина свободного пробега –
,
а средняя длина свободного пробега –
 .
Здесь
.
Здесь
 –
эффективное сечение молекулы,
–
эффективное сечение молекулы,
 – концентрация молекул, которую можно
найти из уравнения Менделеева-Клапейрона
– концентрация молекул, которую можно
найти из уравнения Менделеева-Клапейрона
 :
:
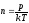 .
Полное число молекул выразим через
концентрацию:
.
Полное число молекул выразим через
концентрацию:
 .
Таким образом, для Z
получаем:
.
Таким образом, для Z
получаем:
 .
Подставим численные значения:
.
Подставим численные значения:
 .
.
Ответ:
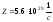 .
.
Задача 2
Вычислить удельные теплоемкости при
постоянном объеме
 и при постоянном давлении
и при постоянном давлении
 неона
и водорода, принимая эти газы за идеальные.
неона
и водорода, принимая эти газы за идеальные.
Решение: Удельные теплоемкости идеальных газов выражаются соотношениями
 и
и
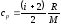 ,
,
где
 - число степеней свободы молекул газа,
M - молярная масса. Для
неона (одноатомный газ)
- число степеней свободы молекул газа,
M - молярная масса. Для
неона (одноатомный газ)
 ,
,
 кг/моль
(см. справочную таблицу). Проведем
вычисления:
кг/моль
(см. справочную таблицу). Проведем
вычисления:


Для водорода (двухатомный газ)
 кг/моль.
Вычислим:
кг/моль.
Вычислим:
 Дж/кг
К;
Дж/кг
К;
 Дж/кг К.
Дж/кг К.
Задача 3
 Кислород
массой 200 г занимает объем 100 л и находится
под давлением 200 кПа. При нагревании газ
расширяется при постоянном давлении
до объема 300 л, а затем его давление
возросло до 500 кПа при неизменном объеме.
Найти изменение внутренней энергии
газа, совершенную им работу и количество
теплоты, переданной газу.
Кислород
массой 200 г занимает объем 100 л и находится
под давлением 200 кПа. При нагревании газ
расширяется при постоянном давлении
до объема 300 л, а затем его давление
возросло до 500 кПа при неизменном объеме.
Найти изменение внутренней энергии
газа, совершенную им работу и количество
теплоты, переданной газу.
 Решение
Решение
График процесса в осях (p,
V) дан на рисунке.
Процесс 1→2 изобарный; работа при
изобарном процессе равна
 .
Процесс 2→3 изохорный, и в этом процессе
работа не совершается. Таким образом,
полная работа
.
Процесс 2→3 изохорный, и в этом процессе
работа не совершается. Таким образом,
полная работа
 .
(1)
.
(1)
Приращение внутренней энергии при переходе газа из состояния 1 в состояние 3:
 .
.
Преобразуем это выражение и используем
уравнение Менделеева-Клапейрона
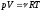 для начального и конечного состояний
газа:
для начального и конечного состояний
газа:
 .
.
Изменение внутренней энергии
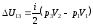 .
(2)
.
(2)
Количество теплоты, переданной газу, найдём из первого начала термодинамики:
 .
(3)
.
(3)
Подставим
в (1), (2) и (3) численные значения:
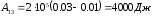 ,
,
 ,
,
 .
.
Ответ:
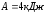 ,
,
 ,
,
 .
.
Задача 4
Найти суммарное изменение энтропии при погружении 100 г нагретого до 3000С железа в воду при температуре 50С. Температуру воды считать постоянной, удельная теплоемкость железа 500 Дж/(кг К).

Решение
Суммарное изменение энтропии воды и
железа равно:
 ,
где
,
где
 - изменение энтропии для воды, поскольку
её температура T0
остаётся неизменной. Количество
теплоты, полученное водой, равно теплоте,
отданной железом при охлаждении:
- изменение энтропии для воды, поскольку
её температура T0
остаётся неизменной. Количество
теплоты, полученное водой, равно теплоте,
отданной железом при охлаждении:
 ,
то есть
,
то есть
 .
.
Температура железа изменяется, поэтому
изменение энтропии для него
 .
Подставим
.
Подставим
 и вычислим интеграл:
и вычислим интеграл:
 .
Полное изменение энтропии:
.
Полное изменение энтропии:
 ,
или
,
или
 .
Подставим численные значения:
.
Подставим численные значения:
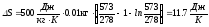 .
.
Ответ:
 .
.
-
Под каким давлением находится в баллоне водород, если емкость баллона 10 литров, а кинетическая энергия поступательного движения всех молекул водорода равна 7.5.103 Дж?
-
Под каким давлением находится газ, если средняя квадратичная скорость его молекул 550 м/с, а плотность 9.10-4 г/см3?
-
Чему равна кинетическая энергия поступательного движения всех молекул, содержащихся в одном моле и в 1 кг гелия при температуре 1000 К?
-
Одноатомный газ массой 1.5 кг находится под давлением 5 атм и имеет плотность 6 кг/м3. Найти энергию теплового движения молекул газа при этих условиях.
-
Определить среднюю квадратичную скорость молекул газа, заключенного в сосуде объемом 2 л под давлением 200 кПа. Масса газа 0.3 г.
-
Какая температура соответствует средней квадратичной скорости молекул углекислого газа, равной 720 км/ч?
-
При какой температуре средняя квадратичная скорость молекул азота больше их наиболее вероятной скорости на 50 м/с?
-
Давление воздуха на уровне моря 750 мм рт.ст., а на вершине горы 590 мм рт.ст. Какова высота горы, если температура воздуха равна 50С?
-
Каким должно быть давление воздуха на дне скважины глубиной 8 км, если считать, что температура по всей высоте постоянна и равна 300 К, а давление воздуха у поверхности земли равно 1 атм?
-
На какой высоте плотность газа составляет 75% от плотности его на уровне моря? Температуру считать постоянной и равной 00С. Задачу решить для: 1) воздуха; 2) углекислого газа.
-
Найти среднюю длину свободного пробега молекул углекислого газа при температуре 1000С и давлении 13.3 Па. Диаметр молекулы 0.32 нм.
-
Найти среднее число столкновений в единицу времени молекулы азота при давлении 53.33 кПа и температуре 270С. Эффективный диаметр принять 0.3 нм.
-
Найти удельную теплоемкость кислорода для: а) V= const; б) p=const.
-
Плотность некоторого двухатомного газа при нормальных условиях =1.43 кг/м3 . Найти удельные теплоемкости cv и cp этого газа.
-
10 г кислорода находится при давлении p=0.3МПа и температуре t=100C. После нагревания при p=const газ занял объем 10 л. Найти количество теплоты, полученное газом, и энергию теплового движения молекул газа до и после нагревания.
-
Найти молярную массу и число степеней свободы молекул газа, если его удельные теплоемкости cv=0.65 Дж/(г.К) и cp=0.91 Дж/(г.К).
-
Определить молярные теплоемкости газа, если его удельные теплоемкости 10.4 кДж/(кг.К) и 14.6 кДж/(кг.К).
-
Кислород занимает объем 1 м3 и находится под давлением 200 кПа. Газ был нагрет сначала при постоянном давлении до объема 3 м3, а затем при постоянном объеме до давления 500 кПа. Найти изменение внутренней энергии газа, совершенную им работу и количество теплоты, переданное газу.
-
Азот массой 200 г расширился изотермически при температуре 280 К, причем объем газа увеличился в 2 раза. Найти изменение внутренней энергии газа, совершенную им работу и количество теплоты, переданное газу.
-
При изотермическом расширении 1 моля кислорода при температуре 300 К ему передано количество теплоты 2 кДж. Во сколько раз увеличился объем газа?
-
Двухатомный газ при давлении 270 кПа имел объем 0.14 м3, а при давлении 320 кПа – объем 0.11 м3. Переход из первого состояния во второе был сделан в два этапа: сначала по изотерме, затем по изохоре. Определить количество поглощенной газом теплоты.
-
Один киломоль газа изобарически нагревается от 200С до 6000С, поглощая 12 МДж теплоты. Найти число степеней свободы молекул газа, приращение внутренней энергии газа, работу газа.
-
В закрытом сосуде объемом 2.5 л находится водород при температуре 170С и давлении 13.3 кПа. Водород охлаждают до 00С. Найти количество отданной газом теплоты, приращение внутренней энергии.
-
Водород занимает объем 10 м3 при давлении 100 кПа. Газ нагрели при постоянном объеме до давления 300 кПа. Найти изменение внутренней энергии газа, совершенную им работу и количество теплоты, переданное газу.
-
При изобарическом нагревании от 0°С до 100°С один моль идеального газа поглощает 3.35 кДж теплоты. Определить отношение удельных теплоемкостей газа, приращение внутренней энергии и работу, совершаемую газом.
-
Азот нагревался при постоянном давлении, при этом ему было сообщено 21 кДж теплоты. Какую работу совершил при этом газ? Каково было при этом изменение внутренней энергии?
-
В цилиндре под поршнем находится 20 г азота. Газ был нагрет на 100°С при постоянном давлении. Определить количество теплоты, сообщенной газу, работу расширения и приращение внутренней энергии.
-
Два киломоля углекислого газа нагреваются при постоянном давлении на 50°С. Найти изменение внутренней энергии, работу расширения и количество теплоты, сообщенное газу (молекула углекислого газа линейная).
-
Газ, совершающий цикл Карно, отдал охладителю 67% теплоты, полученной от нагревателя. Определить температуру охладителя, если температура нагревателя 430 К.
-
Определить работу изотермического сжатия газа, совершающего цикл Карно, КПД которого равен 0.4, если работа изотермического расширения равна 8 Дж.
-
Газ, совершающий цикл Карно, отдал охладителю теплоту 14 кДж. Определить температуру нагревателя, если при температуре охладителя 280 К работа цикла 6 кДж.
-
Найти изменение энтропии 1 моля углекислого газа при увеличении его термодинамической температуры в 2 раза, если процесс нагревания:
1) изохорический; 2) изобарический.
-
При нагревании 1 киломоля двухатомного газа его абсолютная температура увеличилась в 1.5 раза. Найти изменение энтропии, если процесс изобарический.
-
Найти суммарное изменение энтропии при погружении 100 г нагретого до 3000С железа в воду при температуре 50С. Температуру воды считать постоянной, удельная теплоемкость железа 500 Дж/(кг.К).










 ;
;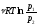
 ;
; 
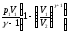 ;
;
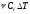 ;
;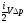
 ;
;

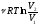 ;
;
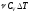
 ;
;
 ;
;
 ;
;
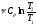 ;
;