
- •2.Расчетная часть
- •2.1 Определение дифференциального уравнения.
- •2.2 Критерий устойчивости Гурвица
- •2.3 Критерий устойчивости Михайлова
- •2.4 Определение областей устойчивости методом d-разбиения.
- •2.5 Расчет амплитудно-фазовых частотных характеристик (афчх)
- •2.5.1 Афх регулятора
- •2.5 Расчет амплитудно-фазовых частотных характеристик (афчх)
- •2.5.1 Афх регулятора
- •2.5.3 Афчх – всей системы
- •2.6 Определение качественных показателей системы
2.Расчетная часть
2.1 Определение дифференциального уравнения.
Параметры регулятора давления:
 ,
сек. = 0,019;
,
сек. = 0,019;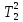 ,
сек. = 0,009;
,
сек. = 0,009; ,
сек. = 0,7;
,
сек. = 0,7;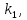 кг/
кг/ = 0,75;
= 0,75; кг/
кг/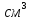 = 10.
= 10.
Для составления уравнений необходимо разбить регулятор на звенья.
Данный регулятор состоит из следующих звеньев:
Колебательного звена (мембрана, пружина)
 +
+
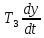 +y = -
+y = -
 x;
x;
 y
+
y
+
 py
+ y = -
py
+ y = - x;
x;
y (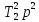 +
+ p
+ 1) = -
p
+ 1) = - x;
(13)
x;
(13)
 =
=
 .
.
Инерционное звено I-го порядка (емкость)
 + y =
+ y =
 x;
x;
 py
+ y =
py
+ y =
 x;
x;
y ( p
+ 1) =
p
+ 1) = x;
(14)
x;
(14)
 =
=
 .
.
Так как данный регулятор состоит из колебательного и инерционного звеньев, которые соединены последовательно, то уравнение всей системы будет иметь следующий вид:
W(p) =
 +
+ +
+ p
+
p
+ +
+ p
+ 1= -
p
+ 1= - (
( ).(15)
).(15)
Подставим свои значения в получившееся уравнение:
W(p)
= 0,009*0,019 +0,019*0,7
+0,019*0,7 +0,019р+0,009
+0,019р+0,009 +0,7р+1=-10*0,75
+0,7р+1=-10*0,75
Получим:
W(p)
= 0,000171 +0,0133
+0,0133 +0,019
+0,019 +0,009
+0,009 +0,7
+0,7 +1=
- 7,5
+1=
- 7,5
W(p)
= 0,000171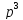 +0,0223
+0,0223 +0,719
+0,719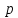 +8,5
= 0
+8,5
= 0
Помножаем на 1000 для удобного использования в решениях
W(p)
= 0,171 +22,3
+22,3 719
719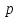 + 8500 = 0
+ 8500 = 0
2.2 Критерий устойчивости Гурвица
Дано характеристическое уравнение
0,171 +22,3
+22,3 719
719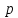 + 8500 = 0
+ 8500 = 0
Составляется таблица

Из данной таблицы образуются
определители:
 ,
, ,
, .
.
 =
=
 = 22,3
= 22,3 0;
0;
 =
=
 = 16033,7 – 1453,5 = 14580,2
= 16033,7 – 1453,5 = 14580,2 0;
0;
 =
=
 = 136286450 – 0 – 12354750 = 123931700
= 136286450 – 0 – 12354750 = 123931700 0.
0.
Вывод: система устойчива,
т.к.
 0,
0, 0,
0, 0, т. е. все коэффициенты положительны.
0, т. е. все коэффициенты положительны.
2.3 Критерий устойчивости Михайлова
Дано характеристическое уравнение
0,171 +22,3
+22,3 719
719 + 8500 = 0
+ 8500 = 0
Заменяем
 на j
на j

0,171 + 22,3
+ 22,3 + 719j
+ 719j + 8500 = 0
+ 8500 = 0
Заменяем
 = -j;
= -j;
 = -1
= -1
-0,171 - 22,3
- 22,3 + 719j
+ 719j + 8500 = 0
+ 8500 = 0
Определяем вещественную и мнимую части
Re(j )
= - 22,3
)
= - 22,3 + 8500
+ 8500
Jm(j )
= -0,171
)
= -0,171 + 719
+ 719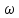
Задаем данные
 .
.
Полученные данные заносим в таблицу 1.
Таблица 1. Значения Re
и Jm при
различных

|
|
0 |
0,1 |
5 |
10 |
17 |
20 |
100 |
500 |
∞ |
|
Re |
8500 |
8499,7 |
7942,5 |
6270 |
2055,3 |
-420 |
-214500 |
-5566500 |
∞ |
|
Jm |
0 |
72 |
3573,6 |
7019 |
11383 |
13012 |
-99100 |
-21015500 |
∞ |
По данным таблицы 1 строим график (смотрите графическую часть, лист 2)
2.4 Определение областей устойчивости методом d-разбиения.
Дано характеристическое уравнение
 + (
+ ( +
+ )
)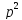 + (
+ ( )
) +𝚔
+ 1 = 0
+𝚔
+ 1 = 0
Запишем уравнение системы
𝚔 = -( +
(
+
( +
+ )
) + (
+ ( )
) + 1) = 0 (16)
+ 1) = 0 (16)
𝚔 = -(0,019 * 0,009 + (0,019 * 0,7 + 0,009)
+ (0,019 * 0,7 + 0,009)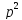 + (0,019 * 0,7)
+ (0,019 * 0,7)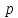 + 1) = 0
+ 1) = 0
Заменяем
 j
j
𝚔 = -0,000171 - 0,0223
- 0,0223 - 0,0133j
- 0,0133j - 1 = 0
- 1 = 0
Заменяем
 = -j;
= -j;
 = -1
= -1
𝚔 = 0,000171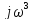 + 0,0223
+ 0,0223 - 0,0133
- 0,0133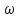 - 1 = 0
- 1 = 0
Определяем вещественную и мнимую части
Re(j )
= 0,0223
)
= 0,0223 – 1
– 1
Jm(j )
= 0,000171
)
= 0,000171 – 0,0133
– 0,0133
Задаем данные
 .
.
Полученные данные заносим в таблицу 2.
Таблица 2. Значения Re
и Jm при
различных
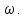
|
|
0 |
1 |
3 |
5 |
18 |
24 |
30 |
36 |
42 |
50 |
|
Re |
-1 |
-0,9 |
-0,7 |
-0,4 |
6,2 |
11,8 |
19 |
27 |
38,3 |
54,75 |
|
Jm |
0 |
-0,01 |
-0,03 |
-0,04 |
0,76 |
2,04 |
4,2 |
7,4 |
12 |
20 |
По данным таблицы 2 строим график (смотрите графическую часть, лист 2)
Вывод: область является устойчивой в пределах (-1;4)


